主成分分析法_数学建模 || 葡萄酒的评价(1)主成分分析法

首先要说一下，这篇文章我在其他的平台发过，也是本人亲自写的，如果大家觉得眼熟的话放弃轻松，没有抄袭，主要是因为与我这 “葡萄酒的评价” 题目成系列了，因此在这里再把这个贴出来。

---

2012 年 A 题葡萄酒的评价，关于评价指标体系的构建，由于变量过多可以使用主成分分析法，对变量进行“降维”处理，使得分析计算结果得到简化。大家今天先学习方法吧，各种方法介绍全了会专门有一篇讲解这些方法在葡萄酒评价题目中的使用。

1

主成分分析法原理

主成分分析法：核心思想是根据原始数据的 n 个变量，重新组合成k个变量，而且这 k 个变量能最大程度的涵盖原始数据的信息。

依据：某一维的方差越大，其所包含的信息越多，也就是说越重要。转换坐标系的方法，可以将二维数据降为一维数据，将三维数据降为二维数据。

主成分分析法，可以通过线性变换的方法将多个变量组合成几个少数的重要变量的多元统计方法。在数学上，这种思想是“降维”。简单的描述一下计算的过程，假设现在有 20 个变量，通过相关性计算，将 20 个变量通过线性表示的方法简化成 4 个新变量，而整理出的4个新变量包含了原来 20  个变量的大部分信息。这句话包含了两个比较重要的点。第一点是整理出出来的是 4 个新变量，也有可能是在 20 个变量中选择出 4 个比较重要的变量。第二点是包含了原变量的大部分信息。而后就可以使用这 4 个新变量进行打分评价，主成分分析法最重要的作用是用于评价。现在可能就会有这么一个问题，既然 20 个变量都有，为什么不直接使用 20 个量进行评价，而是将20个变量简化成了4个新变量。这里就涉及到表述信息的重复。最初的20个变量，可能是从研究主体上直接提取到20个原始数据，可能有两个量之间包含的信息重复，当然也有不同的信息之处。如果第20个变量所展现出来的信息完全可以由其他的19个变量线性表示，那第20个变量的存在完全是没有意义的。这就是在处理中简化变量个数的意义。

新的主成分与原始变量具有不可分割的联系，如下：

1、主成分保留了原始变量绝大多数信息。

2、主成分的个数大大少于原始变量的数目。

3、各个主成分之间互不相关。

4、每个主成分都是原始变量的线性组合。

然后给出一个应用的例子，美国统计学家stone研究国民经济的发展状况，他利用1929年—1938年的的数据得到了17个指标变量，包括雇主补贴，公共支出，利息等，通过主成分分析法，将17个变量简化成了三个新变量，依据自身经济学的背景知识，将三个每变量分别定名为：总收入，总收入变化量，经济发展趋势。这也是主成分分析法需要注意的一个问题，你需要根据背景知识将新变量进行重新命名，这个对于大部分人是很难做到的，也是一个使用受限的一个地方。

2

主成分分析的计算及特点

主成分分析的步骤：

1、初始变量

2、根据初始变量特性选择使用协方差矩阵还是相关矩阵求主成分。

3、计算协方差矩阵或相关矩阵的特征值和特征向量。

①解特征方程，常用雅可比法求出特征值，并使其按大小顺序排列

②分别求出对应于特征值的特征向量

③ 计算主成分贡献率及累计贡献率

④ 计算主成分载荷

⑤ 各主成分的得分

4、确定主成分个数

5、对主成分的含义做解释。

主成分分析的特点：

1、变量间需要有较强相关性，保证能起到很好的降维的效果。

2、新的指标体系无法包含原数据的所有信息。

3、计算前需要进行标准化处理，具体的含义会发生变化，自己进行指标命名时会发生较大的困难。

3

主成分分析的案例分析

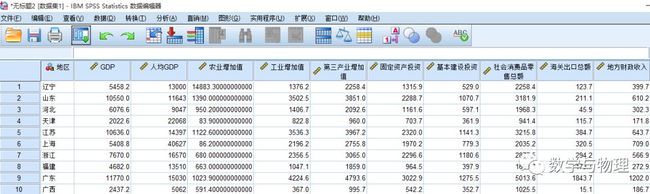
一、从将Excel中的数据导入spss

1、启动spss软件

2、操作一下步骤

3、注意修改文件类型，找到你的文件

4、属性修改

5、完成导入

二、主成分分析步骤

1、如下操作，降维

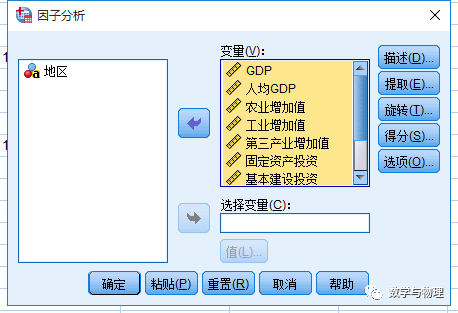
2、将左侧的变量导入到右侧，修改“描述、提取、得分”三项

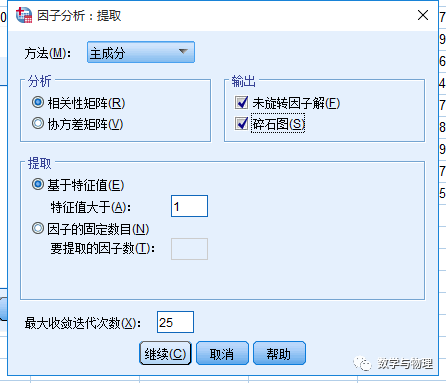
3、修改三项

#描述：

#提取，选中比较直观的碎石图

#得分，选中得分系数矩阵，并点击继续

4、回到初始的界面，点击确定，开始计算

三、计算结果的保存

1、右击，选择导出

2、命名，确定即可

3、在word里可以直接复制分析出来的了

4

主成分分析的计算结果分析

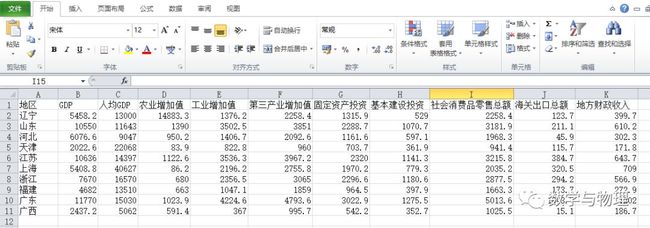
计算结果是很多的图表，这也是说这是个傻瓜软件的原因，通过操作得到这些图表的过程是很简单的，但是能把这些图表分析清楚需要你有一定的统计学的知识背景。原始数据如下：

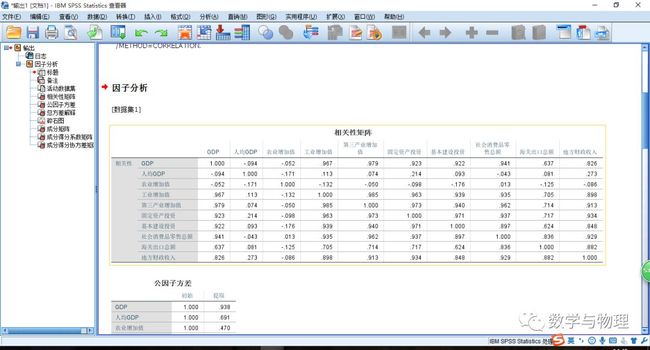
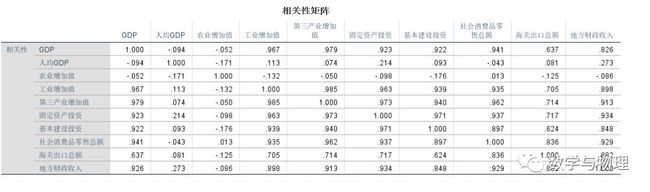
1、相关系数矩阵

相关系数矩阵能表示任意两个指标之间的关系( spss 中，0.01，它只写个 .01)，比如 GDP 跟 GDP 相关性，自身与自身的相关性是1了； GDP 与工业增加值相关性为 0.967 ，大于0.9的数，表示相关性程度已经非常强了。

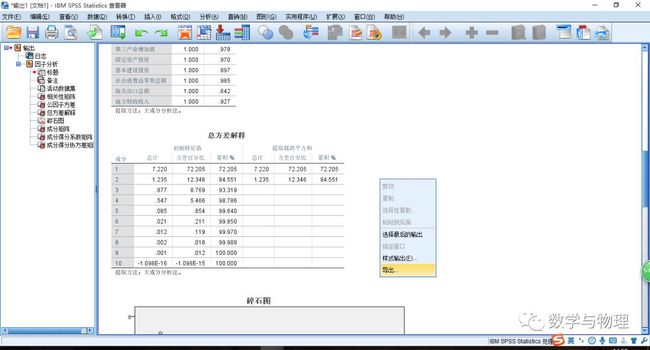
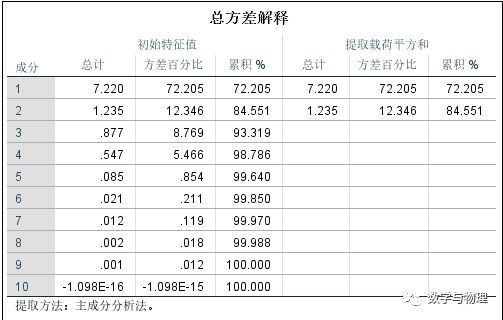
2、总方差解释

总方差解释图表是主成分分析中最重要的一个表格。在这个案例分析汇总，主成分是两个，第一主成分占比重 72.205% (可以这么理解)，第二主成分占比重 12.346% ，这两个主成分达到 85.551% ，超过了 80% ，可以说用这两个指标评价各省份的经济完全可以代替原来的10个指标。碎石图原理基本相同。

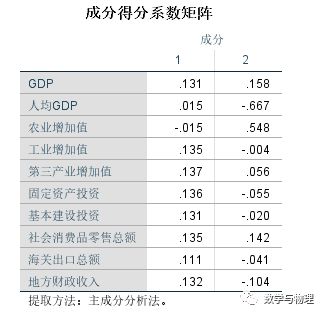
3、系数获取

系数指的是在获得两个主成分后，用 10 个原变量线性表示新的 2 个主变量的过程， spss 软件给出的“成分得分系数矩阵”中可以直接得到系数。

十个变量的位置大家摆清楚，通过以上表格得到这个线性表示的方程，但是大家一定要清楚，由新求出来的 2 个主成分表示总得分的时候一定记得，利用主成分各自占的比重重新求，而不是原来的简单的权重，从下边公式中看的比较清楚，直接看下边的图片吧。

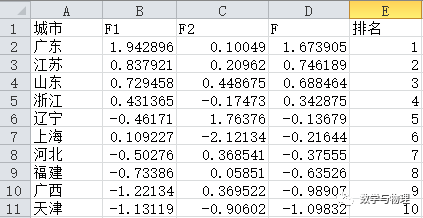
4、计算得分

计算的得分过程也是有很多技巧的，有的人用计算器按，有的人用 Excel 计算，有的人直接拿 MATLAB 矩阵相乘，效率也不一样的，强烈建议大家使用 MATLAB 进行计算，矩阵相乘大家还记得吧，行向量乘以列向量等于位次相同的元素相乘再加和，跟上边这个公式计算过程一模一样，建议大家回去试一试。当然用 Excel 计算也是比较方便。

从结果上看，广东排名第一，江苏次之。但是天津作为直辖市排名第十，原因可以结合题目背景进行讨论，比如人口数量等因素。

大家先把这方法看明白，到最后的时候会综合的联系到 “葡萄酒评价” 一题上。

5

资源分享

本次主要有三个要分享的东西。

1、这次案例用到的原始数据。

2、用到的软件 spss 版本 24，今天的第二篇推文是 spss24 的安装教程。

3、我自己看过的 spss 的教程，简单易懂的那种。

链接:  https://pan.baidu.com/s/1YuGUnIqbampc8Ag6XV8lfg 

提取码:  sv8f 复制这段内容后打开百度网盘手机App，操作更方便哦

撰文 / 科研狗Doggy

排版 / 科研狗Doggy

-数学与物理-原创内容  转载请联系后台

往期精彩回顾

———————————————

经验 | 数学建模中数据归一化处理
狗子荐题| 2012 年 建模国赛 A 题
软件 | MATLAB2014a软件及安装教程

————————————————————————

公众号ID： maths-physics *****************************************数学建模 || 物理学术竞赛

软件安装 || 资料大礼包   

数学、物理的历史  

认知、逻辑的提升