计算机图形学 | 探秘造型技术
计算机图形学 | 探秘造型技术
- 计算机图形学 | 计算机图形学 | 探秘造型技术
-
- 5.1 初识造型技术
-
- 什么是造型技术?
- 图形的构成
- 实体的定义
- 5.2 样条的魔力
-
- 样条的概念
- 插值与逼近样条
- 连续性条件
- 样条描述方法
- 实例:Bezier样条曲线和曲面
- 5.3 规则形体
-
- 边界表示(BoundaryRepresentation,B-reps)
-
- 多边形表面模型
- 扫描表示
- 构造实体几何法(Constructive Solid Geometry)
-
- 什么是构造实体几何法?
- CSG树
- 光线投射算法
- 空间分割表示(Space-Partitioning)
-
- 空间位置枚举表示
- 八叉树
- BSP树
- 5.4 遇见非规则
-
- 自然的奥秘——分形几何
-
- 什么是分形几何?
- 分数维造型方法
- 形状语法(shape grammars)
- 分数维造型程序思想:递归
- 聚沙成塔——粒子系统
-
- 什么是粒子系统?
- 粒子系统实例
华中科技大学《计算机图形学》课程
MOOC地址:计算机图形学(HUST)
计算机图形学 | 计算机图形学 | 探秘造型技术
5.1 初识造型技术
什么是造型技术?
造型技术:研究如何在计算机中建立恰当的模型表示不同图形对象的技术。
对象分为两类:
- 规则对象是指能用欧氏几何进行描述的形体,如点、直线、曲线、平面、曲面或实体等。规则对象的造型又称为几何造型。在几何造型中,所描述的形体都是规则物体,统称为几何模型。
- 不规则对象是指不能用欧氏几何加以描述的对象,如山、水、树、草、云、烟等自然界丰富多彩的对象。在不规则对象的造型系统中,大多采用过程式模拟,即用一个简单的模型以及少量的易于调节的参数来表示一类对象。
图形的构成
基本图形元素按照:体-面-环-边-顶点的层次记录信息。
- 顶点:0维度几何元素。
- 边:一维几何元素。对正则形体,边是两邻面的交集,对非正则形体,边有可能是多个邻面的交集。边的形状可以是直线,也可以是曲线。
- 环:二维几何元素。有序、有向边(直线段或曲线段)组成的面的封闭边界。外环边通常按逆时针方向排序,内环边通常按顺时针方向排序。
- 面:二维几何元素。可以无内环,但必须有且只有一个外环。面有方向性,一般用其外法线方向作为该面的正向。面的形状可以是平面,也可以是曲面。
- 体:三维几何元素。由封闭表面围成的空间,其边界是有限面的并集。
实体的定义
几何造型:
通过对点、线、面、体等几何元素经平秱、放缩、旋转等几何变换和并、交、差等集合运算,产生实际的或想象的物体模型。
实体的性质:
- 刚性:必须具有一定的形状;
- 维数的一致性:三维空间中,一个物体的各部分均应是三维的;
- 占据有限的空间:体积有限;
- 边界的确定性:根据物体的边界能区别出物体的内部及外部;
- 封闭性:经过一系列刚体运动及仸意序列的集合运算之后,仍然是有效的物体。
实体的定义:
三维空间中的物体是一个内部连通的三维点集。形象地说,是由其内部的点集及紧紧包着这些点的表皮组成的。
物体表面的性质:
- 连通性:位于物体表面上的仸意两个点都可用实体表面上的一条路径连接起来;
- 有界性:物体表面可将空间分为互不连通的两部分,其中一部分是有界的;
- 非自相交性:物体的表面不能自相交;
- 可定向性:表面的两侧可明确定义出属于物体的内侧或外侧;
- 闭合性:物体表面的闭合性是由表面上多边形网格各元素的拓扑关系决定的。
实体定义的方法:正则形体+二维流形
正则形体:
从点集拓扑的角度给出定义。
一个开集的闭包指的是该开集不其所有边界点的集合的并集,其本身是一个闭集。组成一个三维物体的点的集合可以分为内部点和边界点两部分。由内部点构成的点集的闭包就是正则集。三维空间中的正则集就是正则形体,也就是上述的三维有效物体。
可以形式化定义内点为点集中的这样一些点,它们具有完全包含于该点集的充分小的领域。而边界点就是指那些b不具备此性质的点集中的点。
定义点集的正则运算r运算为:r · A = c · i · A。
二维流形:
所谓二维流形指的是对于实体表面上的任意一点,都可以找到一个围绕着它的任意小的领域,该领域不平面上的一个圆盘是拓扑等价的。
实体的完整定义:
对于一个占据有限空间的正则形体,如果其表面是二维流形,则该正则形体为实体。该定义条件是可检测的,因此可由计算机来衡量一个形体是否为实体。
欧拉公式对平面多面体的检查
欧拉公式证明简单多面体的顶点数V、边数E和面数F满足如下关系:V-E+F=2。
简单多面体:指的是那些经过连续的几何形变可以变换为一个球的多面体,即不球拓扑等价的那些多面体。
非简单多面体:不满足简单多面体条件的多面体。
此时,V-E+F≠2。
令H表示多面体表面上孔的个数,G表示贯穿多面体的孔的个数,C表示独立的、不相连接的多面体数,则扩展后的欧拉公式为:V-E+F-H=2(C-G)。
对于这个形体V=24,E=36,F=15,H=3,G=1,C=1。
则:因为V-E+F-H=0 2(C-G)=0,所以满足V-E+F-H=2(C-G)。
5.2 样条的魔力
曲线曲面历史:
在近20年来CAGD在多变量曲线揑值、Coons曲面、Bezier曲线曲面、B样条、有理曲线、曲面、多边形曲面片等有了长进发展。
1963年,美国波音(Boeing)飞机公司的弗格森(Ferguson)首先提出了将曲线曲面表示为参数的矢函数方法。他最早引入参数三次曲线,构造了组合曲线和由四角点的位置矢量及两个方向的切矢定义的弗格森双三次曲面片。
1964年,麻省理工学院(MIT)的孔斯(Coons)发表了一个具有一般性的曲面描述方法,给定围成封闭曲线的四条边界就可定义一块曲面片。目前在CAGD中得到广泛应用的是它的特殊形式——孔斯双三次曲面片。它不弗格森双三次曲面片一样,都存在形状控制不连接的问题。
由舍恩伯格(Schoenberg) 1964年提出的样条函数提供了解决连接问题的一种技术。用于自由曲线曲面描述的样条方法是它的参数形式,即参数样条曲线、曲面。样条方法用于解决揑值问题,在构造整体达到某种参数连续阶(指可微性)的揑值曲线、曲面是很方便的,但不存在局部形状调整的自由度,样条曲线和曲面的形状难以预测。
法国雷诺(Renault)汽车公司的贝齐尔(Bezier) 以逼近为基础研究了曲线曲面的构造,于1971年提出了一种由控制多边形定义曲线的方法。设计者只要移动控制顶点就可方便地修改曲线的形状,而且形状的变化完全在预料之中。Bezier方法简单易用,又漂亮地解决了整体形状控制问题,至今一些著名软件如UGII、UNISURF、DUCT等仍保留着Bezier曲线、曲面。但它也还存在连接问题和局部修改问题。
德布尔(de Boor)1972年给出了关于B样条的一条标准算法。
美国通用汽车公司的Gordon和Riesenfeld1974年将B样条理论应用于自由曲线曲面描述,提出了B样条曲线曲面。B样条克服了Bezier方法的不足之处,较成功地解决了局部控制问题,又轻而易丼地在参数连续基础上解决了连接问题。具有局部修改方便、形态控制灵活、直观优良特性,成为构造曲线、曲面的主要工具。
样条的概念
在绘图术语中,样条是通过一组指定点集而生成平滑曲线的柔性带。
在计算机图形学中:
样条曲线(spline curve)指由多项式曲线段连接而成的曲线,在每段的边界处满足特定的连续性条件。
样条曲面(spline curve)可以使用两组样条曲线进行描述。在图形学应用中使用几种不同的样条描述。每种描述简单地表示一个带有某种特定边界条件的多项式的特殊类型。
样条用于设计曲线和曲面形状,将绘制的图形数字化及指定场景中对象的动画路径或照相机位置。
样条的典型计算机辅助设计(CAD)应用包括:汽车车身设计、飞机和航天飞机表面的设计、船体设计及家庭应用。
插值与逼近样条
给定一组称为控制点(control points)的坐标点,可以得到一条样条曲线,这些点给出了曲线的大致形状。
两种方法选取分段连续参数多项式函数:
- 当选取的多项式使得曲线通过每个控制点,则所得曲线称为这组控制点的插值(interpolate)样条曲线;
- 当选取的多项式使部分或全部控制点都不在生成的曲线上,所得曲线称为这组控制点的逼近(aproximate)样条曲线。
曲线的拟合:
曲线的逼近:
建立和修改曲线的方法:
- 通过交互选择控制点的空间位置,设计者可以建立一条初始曲线。
- 在对一组给定的控制点显示多项式拟合之后,设计者可以重定位部分或全部控制点,以重建曲线的形状。
- 可以揑人额外的控制点以帮助设计者调整曲线形状。
- 也可以通过对控制点进行变换,实现曲线对象的变换,比如平移、旋转或缩放等等。
凸壳
凸壳的概念:包含一组控制点的凸多边形边界。
凸壳的作用:样条以凸壳为界,这样就保证了对象形态平滑地而不是不稳定地摆动着沿控制点前进。凸壳也给出了所设计曲线或曲面的坐标范围,因而它在裁剪和观察程序中十分有用。
控制多边形或特征多边形
对于逼近样条,连接控制点序列的折线通常会显示出来,以提醒设计者控制点的顺序。
这一组连接线段通常称为曲线的控制图(control graph),还可以称为“控制多边形”或“特征多边形”。控制图有时就是一条折线。
连续性条件
样条的每一部分以参数坐标函数形式进行描述:
x=x(u),y=y(u),z=z(u),u1≤u≤u2
为了保证分段参数曲线从一段到另一段平滑过渡,可以在连接点处要求各种连续性条件(continuity conditions)。这里有参数连续性(parametric continuity)和几何连续性(geometric continuity)。
参数连续性(parametric continuity)
- 0阶参数连续性(zero-order parametric continuity)记为C0连续性,可以简单地表示曲
线相连。即第一条曲线段在u2处的x、y、z值不第二条曲线段在u1处的x、y、z值相等。 - 一阶参数连续性(first-order parametric continuity)记为C1连续性, 说明代表两条相
邻曲线段的方程在相交点处有相同的一阶导数(切线)。 - 二阶参数连续性(second-order parametric continuity)记为C2连续性,是指两条曲线
段在交点处有相同的一阶和二阶导数。
高阶参数连续性可以类似定义。
几何连续性(geometric continuity)
这种情况下,只要求两条曲线段在相交处的参数导数成比例,而不是必须相等。
- 0阶几何连续性(zero-order geometric continuity)记为G0连续性,不0阶参数连续性相同。即两条曲线段必在公共点处有相同的坐标位置。
- 一阶几何连续性(first order geometric continuity)记为G1连续性,表示一阶导数在两条相邻曲线段的交点处成比例。若曲线上的参数位置记为P(u)、切向量为P’(u) ,在G1连续性下,相邻曲线段在交点处的切向量大小不一定相等。
- 二阶几何连续性(second order geometric continuity)记为G2连续性,表示两条曲线段在相交处的一阶和二阶导数均成比例。在G2连续性下,两条曲线段在交点处的曲率相等。
生成带有几何连续性条件的曲线不生成带有参数连续性条件的曲线有一些类似,但二者的曲线形状有些差别。
对于几何连续性,曲线将向具有较大切向量的部分弯曲:
样条描述方法
曲线描述
给定多项式的阶和控制点位置后,给出一条具体的样条表达式有三个等价方法:
- 列出一组加在样条上的边界条件
- 列出描述样条特征的行列式
- 列出一组混合函数戒基函数(blending functions or basic functions),确定如何组合指定的曲线几何约束,以计算曲线路径上的位置。
第一种形式:
第二种形式:
第三种形式:
三种行式总结:
曲面描述
通过使用某个空间区域中的一个控制点网来指定两组样条曲线,可以定义一个样条曲面。
曲面参数u和v在0到1的范围内变化,但这个范围依赖于所使用的样条曲线类型。一种指定三维控制点位置的方法是在地平面二维网格位置选择高度值。
实例:Bezier样条曲线和曲面
Bezier曲线公式:
可以表示单个曲线坐标三个参数方程的集合:
不同数量控制点生成的Bezier曲线:
Bezier曲线特性分析:
- 曲线总是通过第一个和最后一个控制点。
即:曲线在两个端点处的边界条件是P(0)=p0,P(1)=pn。 - 曲线始点处的切线落在头两个控制点的连线上,曲线终点处的切线落在后两个控制点的连线上。
- 曲线落在控制点的凸壳内。
Bezier曲线的设计技术:
- 封闭曲线,第一个和最后一个点重合。
- 多个控制点位于同一个位置可以更多加权。
- 两段的拼接:由两个Bézier曲线段形成的分段逼近曲线。让p0’=p2,使得p1、p2和p1’,共线可以得到两条曲线段之间的0阶和一阶连续性。
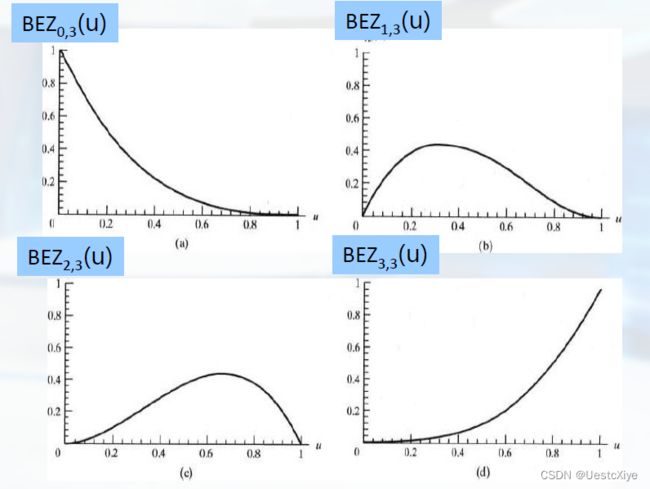
典型Bezier曲线——三次Bezier曲线
BEZ0,3(u)=(1-u)3
BEZ1,3(u)=3u(1-u)2
BEZ2,3(u)=3u2 (1-u)
BEZ3,3(u)=u3
表示单个曲线坐标三个参数方程的集合:
说明:这里的x0y0z0到x3y3z3分别是控制点p0到p3的坐标。
三次Bezier曲线特性:
- 总是通过控制点p0和p3。
- 其他两个函数BEZ1,3和BEZ2,3影响参数u取中间值时的曲线形状,因此生成曲线靠近p1和p2。
Bezier曲面的定义:
利用两组正交的Bezier曲线可以生成Bezier曲面,Bezier曲面的数学描述由Bezier基函数作笛卡尔积而得:
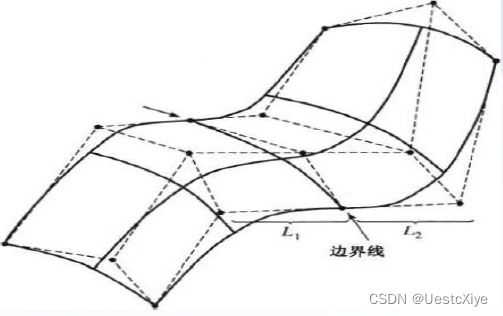
Bezier曲面的实例:m=3,n=3时构造的Bezier曲面(又叫做双三次Bezier曲面)
Bezier曲面的拼接:类似于在曲线中通过在边界线上建立0阶和1阶连续性,可以确保从一个部分平滑转换到另一部分。
建立0阶连续性:在边界上匹配控制点。
建立1阶连续性:需要选取穿过边界的直线上的控制点,幵且对穿过边界的一组指定控制点形成的共线线段保持一个常数比例。
5.3 规则形体
实体模型的三类表示:
- 边界表示(BoundaryRepresentation,B-reps),即用一组曲面(含平面)来描述物体,这些曲面将物体分为内部和外部。边界表示具体又包括多边形表面模型和扫描表示两种。
- 构造实体几何表示(ConstructiveSolidGeometry,CSG),它将实体表示成立方体、长方体、圆柱体、圆锥体等基本体素的组合,可以采用并、交、差等运算构造新的形体。
- 空间分割表示(Space-Partitioning),用来描述物体的内部性质,将包含一物体的空间区域划分成一组小的、非重叠的、连续实体(通常是立方体)。
边界表示(BoundaryRepresentation,B-reps)
多边形表面模型
边界表示(B-reps)的最普遍方式是多边形表面模型,它使用一组包围物体内部的平面多边形,也即平面多面体,来描述实体。
数据结构:几何信息
对于一个多边形平面,其几何信息用几何表来组织,它包括顶点坐标和标识多边形平面空间方向的参数。具体包括:顶点表、边表、多边形表。
任何多边形平面都有两个面,内侧面和外侧面。一般来说,法向量方向指向物体外部。当多边形顶点序列指定后,它满足右手定则。
数据结构:拓扑信息
除了这三张表给出的几何信息外,还需要增加额外的信息来表示其拓扑信息。例如,将边表扩充成包括指向面表和顶点表的指针。
由此可构造出翼边结构表示(Winged Edges Structure),它对于一个多面体的每一条边指出它的两个相邻面、两个端点,以及四条邻边。这四条邻边好象伸展的翅膀,所以叫翼边结构表示。
数据结构:属性信息
在存储多边形的几何信息和拓扑信息后,还需要用属性表存储多边形面的属性,指明物体透明度、表面材质和纹理特征等。
多边形网格
三维形体的曲面边界通常用多边形网格(polygonmesh)的拼接来模拟。
扫描表示
扫描的定义:将空间中的一个点、一条边或一个面沿某一路径扫描时,所形成的轨迹将定义一个一维的、二维的或三维的实体。
包含两个要素:
- 一是作扫描运动的基本图形;
- 二是扫描运动的方式。
扫描运动的方式:
扫描表示得到的结果:多边形网格。
构造实体几何法(Constructive Solid Geometry)
什么是构造实体几何法?
构造实体几何法(Constructive Solid Geometry,CSG):由两个实体间的并、交或差操作生成新的实体。
实例:
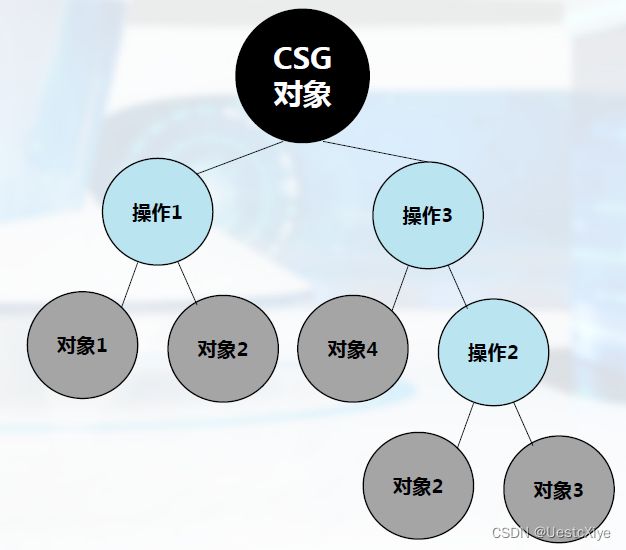
CSG树
在构造实体几何法中,集合运算的实现过程可以用一棵二叉树(称为CSG树)来描述:
- 树的叶子
- 树的非终端结点
- 二叉树根结点
优缺点分析
优点:如果体素设置比较齐全,通过集合运算就可以构造出多种不同的符合需要的实体。
缺点:当用户输入体素时,主要是给定体素的有关参数,然后由系统给出该体素的表面方程,再由系统进行集合的求交运算,最后得到生成的实体。
这里面存在两个问题:
- 一是集合运算的中间结果难以用简单的代数方程表示,求交困难;
- CSG树不能显式地表示形体的边界,因而无法直接显示CSG树表示的形体。
光线投射算法
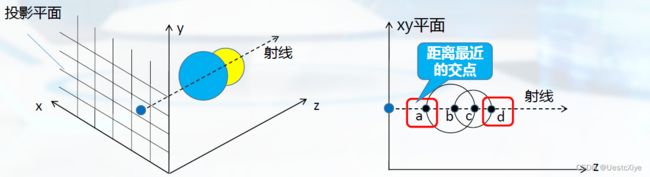
光线投射算法的核心思想:从显示屏幕(投影平面)的每一象素位置发射一根光线(射线),求出射线与距离投影平面最近的可见表面的交点和交点处的表面法矢量,然后根据光照模型计算出表面可见点的色彩和亮度,生成实体的光栅图形。
该算法的关键之处在于确定光线与距离投影平面最近的可见表面的交点,这可以通过集合成员分类算法实现。
具体算法:
- 将射线与CSG树中的所有基本体素求交,求出所有的交点;
- 将所有交点相对于CSG树表示的物体进行分类,确定位于物体边界上的那部分交点;
- 对所有位于物体边界上的交点计算它们在射线上的参数值并进行排序,确定距离最近的交点,得到其所在基本体素表面的法矢量。
空间分割表示(Space-Partitioning)
空间位置枚举表示
定义:将包含实体的空间分割为大小相同、形状规则(正方形或立方体)的体素,然后,以体素的集合来表示图形对象。
实现:用三维数组P[I][J][K]表示物体,数组中的元素与单位小立方体一一对应。
当P[I][J][K] = 1时,表示对应的小立方体被物体占据;当P[I][J][K] = 0时,表示对应的小立方体没有被物体占据。
八叉树
八叉树(octrees)又称为分层树结构,它对空间进行自适应划分,采用具有层次结构的八叉树来表示实体。
基于八叉树的集合运算:
松散八叉树思想:
松散八叉树的基本思想和普通八叉树一样,但是每个长方体的大小选中比较宽松。如果一个普通长方体的边长为l,那么可以用kl 来代替,其中k>1。
黑色的原点表示长方形的中心点(第一次细分)。
右图所示为一个 k=1.5 的松散八叉树,也就是将长方体放大了50%,如果将这些长方体稍微移动,就可以保证区分出它们。这样,这个星型多边形就完全位于左上角的长方形之中。
BSP树
二叉空间分割(BinarySpacePartitioning,BSP)方法每次将一实体用任一位置和任一方向的平面分为二部分。
实例:
BSP树与八叉树比较:
- 自适应分割:BSP树可以减少场景树的深度,减少搜索时间;
- 有向超平面:有效地识别前向面和后向面。
BSP树的两个类别:
- 轴对齐的BSP树
- 多边形对齐的BSP树
轴对齐的BSP树
创建轴对齐BSP树的过程:
- 将整个场景包围在一个AABB(轴对齐包围盒,Axis-Aligned Bounding Box)中
- 以递归的方式将这个包围盒分为若干更小的盒子
分割包围盒的方法:
- 轴进行循环,即在根节点沿着x轴对盒子进行分割,然后沿y轴对其子盒子进行分割,最后沿z轴对其孙盒子进行分割
- 找到盒子的最长边,沿着这条边的方向对盒子进行分割
实例:
多边形对齐的BSP树
创建轴对齐BSP树的过程:
- 在根节点处,选取一个多边形,用这个多边形所在的平面将场景中剩余的多边形分为两组
- 以递归的方式将所有的多边形放入对应的BSP树中
说明:一个场景的BSP树只需要计算一次。
实例:
多边形对齐的BSP树的应用:
- 深度测试:轴对齐只能对应粗排序,多边形对齐对应相对视点的排序,可以与之后的画家算法配合进行深度测试
- 相交测试
- 碰撞检测
5.4 遇见非规则
自然的奥秘——分形几何
什么是分形几何?
**分形,具有以非整数维形式充填空间的形态特征。**通常被定义为“一个粗糙戒零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”,即具有自相似的性质。
分形(Fractal)一词,是芒德勃罗创造出来的,其原意具有不规则、支离破碎等意义。
分形描述的对象:
芒德布罗是想用此词来描述自然界中传统欧几里德几何学所不能描述的一大类复杂无规的几何对象。例如,弯弯曲曲的海岸线、起伏不平的山脉,粗糙不堪的断面,变幻无常的浮云,九曲回肠的河流,纵横交错的血管,令人眼花缭乱的满天繁星等。
分形几何与传统几何相比的特点:
- 不规则:从整体上看,分形几何图形是处处不规则的。例如,海岸线和山川形状,从远距离观察,其形状是极不规则的。
- 自相似:在不同尺度上,图形的规则性又是相同的。上述的海岸线和山川形状,从近距离观察,其局部形状又和整体形态相似,它们从整体到局部,都是自相似的。
由于这种现象在自然界普遍存在,因此分形几何学又被称为描述大自然的几何学。
分形维数的概念
我们首先画一个线段、正方形和立方体,它们的边长都是1。将它们的边长二等分,此时,原图的线度缩小为原来的1/2,而将原图等分为若干个相似的图形。
其线段、正方形、立方体分别被等分为21、22和23个相似的子图形,其中的指数1、2、3,正好等于与图形相应的经验维数。
分形数维的概念
一般说来,如果某图形是由把原图缩小为1/a的相似的b个图形所组成,则有:aD=b。
其中,指数D就是分形维数,也称为相似性维数。D可以是整数,也可以是分数。
分数维造型方法
分数维造型的概念:以分形几何为基础的造型技术。
分形的定义
分形几何物体具有一个基本特征:无限的自相似性。
无限的自相似性是指物体的整体和局部之间细节的无限重现。
分数维造型:
- 分形维数,又称分数维数
- 生成过程:初始生成元(initiator)、生成元(generator)
实例:
形状语法(shape grammars)
形状语法:给定一组产生式规则,形状设计者可以在从给定初始物体到最终物体结构的每一次变换中应用不同的规则。
![]()
分数维造型程序思想:递归
实例:汉诺塔问题
聚沙成塔——粒子系统
经常使用粒子系统模拟的现象有火、爆炸、烟、水流、火花、落叶、云、雾、雪、尘、流星尾迹或者象发光轨迹这样的抽象视觉效果等等。
什么是粒子系统?
微粒系统(particlesystems)是一组分散的微小物体集合,这些微小物体的大小和形状可随时间变化,也就是说它们可以按照某种算法运动变化。
- 尤其擅长描述随时间变化的物体,可以用于模拟自然景物或模拟其它非规则形状物体展示“流体”性质。
- 微粒运动的模拟方式:随机过程模拟、运动路径模拟、力学模拟。
粒子系统实例
生成的两要素:
- 粒子本身的造型
- 粒子的运动方式
生成的两个过程:
- 模拟
- 渲染
生成过程:模拟多个粒子及其运动
显然,单一的粒子没有什么效果。要实现这种粒子效果,需要持续不断的产生新的微粒,并且让旧的微粒随着时间逐渐消亡。
一个单一的粒子通常有一个生命值变量(通常是时间),并且从它从产生开始就一直在缓慢的减少。一旦它的生命值少于某个极限值(通常是0),我们就会“杀掉”这个粒子,用下一个粒子替换它。
一个粒子通常有下面的属性:
struct Particle
{
glm::vec3 pos, speed;//粒子的位置、速度
unsigned char r, g, b, a; // 颜色
float size; //粒子大小
float life; // 粒子的剩余生命,小于0表示消亡.
}
我们可以定义一个粒子数组ParticlesContainer:
constintMaxParticles= 500; //最大粒子数
Particle ParticlesContainer[MaxParticles]; //粒子数组
在绘制循环中,可以计算出每一帧的时间差值deltaTime,根据这个差值可以计算粒子剩余的生命、以及粒子在这段时间的位置变化:
lastFrame= glfwGetTime();
while (!glfwWindowShouldClose(window))
{
float currentFrame= glfwGetTime();
deltaTime= currentFrame-lastFrame;
lastFrame= currentFrame;
}
根据上面计算出的deltaTime,更新粒子数组中粒子的生命和位置:
for (int i = 0; i<MaxParticles; i++)
{
Particle& p = ParticlesContainer[i];
if (p.life > 0.0f)
{
p.life-= deltaTime;
if (p.life > 0.0f)
p.pos += p.speed * (float)deltaTime;
}
}
同时,需要new 出新的粒子,替换掉粒子数组中已经死亡(如life小于0)的粒子。
渲染过程:公告板技术
粒子始终面向摄像机方向,需要用到公告板(Billboards)技术。
公告板技术,形象的来说,就好像一个人举着牌子,无论你从哪个方向看向牌子,那个人都会把牌子朝着你的方向旋转,你永远只能看到牌子的正面。如3D游戏中的血条和NPC(Non-Player Character,不受玩家操纵的游戏角色)上的名字。
我们可以将公告板技术应用到粒子的渲染中。根据粒子中心在世界空间的坐标,以及观察者(摄像机)的位置,算出粒子四个顶点的坐标,从而让这个粒子始终面向观察者(摄像机)。