聚类效果评测-Fmeasure和Accuracy及其Matlab实现

聚类结果的好坏，有很多种指标，其中F-Measue即F值是常用的一种，其中包括precision(查准率或者准确率)和recall(查全率或者召回率)。

F-Measue是信息检索中常用的评价标准。

F-Measue的公式如下：

\[{{F}_{\beta }}=\frac{\left( {{\beta }^{2}}+1 \right)P\cdot R}{{{\beta }^{2}}\cdot P+R}\]

其中${\beta}$是参数，P是precision,R是reacll。通常${\beta}$取1，即：

\[F=\frac{2\cdot P\cdot R}{P+R}\]

设人工标记的分类簇为${{P}_{j}}$，聚类算法分类簇为${{C}_{i}}$ 

 precision、recall个人感觉准确率和查全率翻译的更方便理解些。

                                                                     

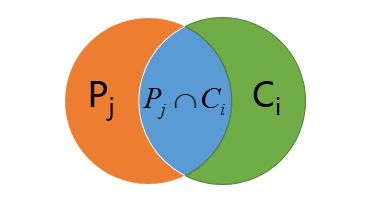
precision(查准率或者准确率)：

\[P({{P}_{j}},{{C}_{i}})=\frac{\left| {{P}_{j}}\cap {{C}_{i}} \right|}{\left| {{C}_{i}} \right|}\]

recall(查全率或者召回率)：

\[R({{P}_{j}},{{C}_{i}})=\frac{\left| {{P}_{j}}\cap {{C}_{i}} \right|}{\left| {{P}_{j}} \right|}\]

F-Measure:

\[F\left( {{P}_{j}},{{C}_{i}} \right)=\frac{2\times P({{P}_{j}},{{C}_{i}})\times R\left( {{P}_{j}},{{C}_{i}} \right)}{P\left( {{P}_{j}},{{C}_{i}} \right)+R\left( {{P}_{j}},{{C}_{i}} \right)}\]

获得一个矩阵，不同于信息检索的是F-Measure有多个，并且人工标记簇的个数和聚类算法得到的簇个数不一定相等。

                                                          

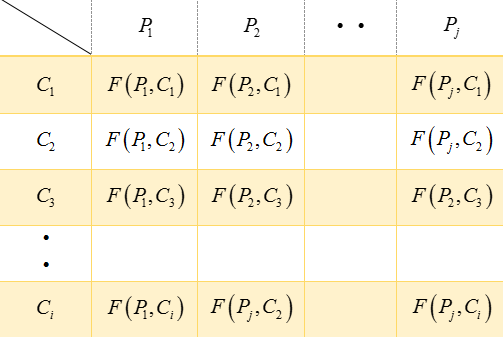
若已人工标记的簇${{P}_{j}}$为基准，则聚类算法结果越接近人工标记的结果效果越好。也是推荐使用的指标

针对每一个人工标记的${{P}_{j}}$选择${{C}_{i}}$中最接近的作为其F值：

\[F\left( {{P}_{j}} \right)=\underset{1\le i\le m}{\mathop{\max }}\,F({{P}_{j}},{{C}_{i}})\]

然后对所得到的F值进行加权平均，得到最终的一个直观的F值

\[F=\sum\limits_{j=1}^{S}{{{w}_{j}}\cdot F\left( {{P}_{j}} \right)},\ {{w}_{j}}=\frac{\left| {{P}_{j}} \right|}{\sum\limits_{i=1}^{s}{\left| {{P}_{i}} \right|}}=\frac{\left| {{P}_{j}} \right|}{n}\]

代码：

function [FMeasure,Accuracy] = Fmeasure(P,C)

% P为人工标记簇

% C为聚类算法计算结果

N = length(C);% 样本总数

p = unique(P);

c = unique(C);

P_size = length(p);% 人工标记的簇的个数

C_size = length(c);% 算法计算的簇的个数

% Pid,Rid：非零数据：第i行非零数据代表的样本属于第i个簇

Pid = double(ones(P_size,1)*P == p'*ones(1,N) );

Cid = double(ones(C_size,1)*C == c'*ones(1,N) );

CP = Cid*Pid';%P和C的交集,C*P

Pj = sum(CP,1);% 行向量，P在C各个簇中的个数

Ci = sum(CP,2);% 列向量，C在P各个簇中的个数



precision = CP./( Ci*ones(1,P_size) );

recall = CP./( ones(C_size,1)*Pj );

F = 2*precision.*recall./(precision+recall);

% 得到一个总的F值

FMeasure = sum( (Pj./sum(Pj)).*max(F) );

Accuracy = sum(max(CP,[],2))/N;

end