【图嵌入】Graph Embedding 方法之 LINE 原理解读

LINE 出自论LINE: Large-scale Information Network Embedding，与 DeepWalk 相比，比较明显的区别在于：

1. DeepWalk 使用的深度优先搜索策略，而 LINE 使用了广度优先搜索策略。
2. DeepWalk 仅适用于无权图，而LINE模型适用于带权图与无权图。

下图展示了一个简单的图，图中的边既可以是有向的，也可以是无向的，并且边的粗细程度也代表了权重的大小：

一阶相似度

作者认为可以用一阶相似度描述图中成对顶点之间的局部相似度，连接两个节点的边权重越大，则一阶相似度越高。若两个节点之间不存在边，则认为一阶相似度为 0。例如图中的节点６、７在低维空间中应该是比较靠近的，因为连接二者的边具有很大的权重，而5、6之间则的一阶相似度则为0。

为了能够通过节点的低维向量表示一阶相似度，我们还需要定义一个优化目标。假设用 $u_i,u_j$ 作为节点的低维向量表示(Embedding向量)，那么一阶相似度的计算就转换为学习一种函数映射 $f(u_i,u_j)$，使得其映射结果可以表示边的权重。对于每一条无向边 $(i,j)$，定义顶点 $v_i,v_j$ 的联合概率密度为：
$$p_1(v_i,v_j)=\frac{1}{1+exp(-u_i^T\cdot u_j)}$$
如果两个向量相似，则内积的结果也相对比较大，将内积结果作为 sigmoid 函数的输入，最终得到两个节点的联合概率分布 $p_1(v_i,v_j)$。

在得到联合概率分布之后，还需要一个“参照物”来指导它的学习，论文中将两个节点之间边的权重占比视为经验分别，并将它作为学习目标：
$$\begin{gathered} {\hat{p}}_1(i,j)=\frac{w_{ij}}{W} \\ W=\sum _{(i,j)\in E}{w}_{ij} \end{gathered}$$
于是最终的优化目标是使得联合概率分布尽量接近经验分布，而K-L散度可以表示数据原始分布p和近似分布q之间的对数差值的期望，因此只要优化 $p_1(v_i,v_j)$ 与 ${\hat{p}}_1$ 的K-L散度(忽略常数项)，就能使二者的分布尽可能相似：
$$O_1=-\sum _{(i,j)\in E}{w}_{ij}log(p_1(v_i,v_j))$$

二阶相似度

一阶相似度固然可以直接表示节点之间的相似性，但是在真实环境下的信息网络往往存在大量的信息缺失，而许一阶相似度为0的节点，他们本质上相似度也很高。

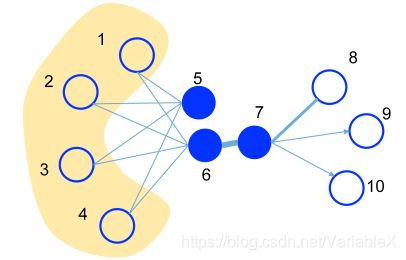
仔细观察节点5、6，发现他们具有非常相似的邻居节点(1，2，3，4)，这其实也表明5、6两个节点应该是相似的，作者使用二阶相似度来描述这样的关系，若两个节点不存在共同的邻居节点，则二阶相似度为0。这意味着，如果节点5的低维向量表示同时与节点1，2，3，4的低维向量表示相似，并且节点6的低维向量表示同时与节点1，2，3，4的低维向量表示相似，那么节点5与6的低维向量表示也就是相似的。

根据一阶相似度的理论，我们可以将两个节点的向量内积 用sigmoid函数转换为概率 来表示两个节点间边的权重。但是在二阶相似度的表示问题中，我们需要表示一个节点与周围多个context节点的相似度，那么就可以使用 softmax 函数将某个节点与周围节点向量内积的结果转换为概率。给定节点 $v_i$ 产生节点 $v_j$ 的概率为：
$$p_2(v_j|v_i)=\frac{exp(u_j^{{}^{\prime }T}\cdot u_i)}{{\sum }_{k=1}^{|V|}exp(u_k^{{}^{\prime }T}\cdot u_i)}$$

其中，$u_i,u_j^{\prime }$ 为节点 $i,j$ 低维向量表示，且 $u_j^{\prime }$ 为节点 j 表示为上下文时的向量表示。$|V|$ 表示图中所有节点的个数。当节点 $k,i$ 之间没有邻接关系时，二者向量的内积也就比较小，在理想情况下当两个节点没有边相连时，$exp(u_k^{{}^{\prime }T}\cdot u_i)\to 0$，此时 $p_2(v_j|v_i)$ 仅仅受到节点 $i$ 周围邻居节点的影响。 不难发现，这个公式将节点 $i$ 与邻居节点的相似度转换为条件概率。

再定义经验分布为：
$${\hat{p}}_2(v_j|v_i)=\frac{w_{ij}}{d_i}$$
其中，$w_{ij}$ 是边 $(i,j)$ 的权重，$d_i={\sum }_{k\in N(i)}{w}_{ik}$，$N(i)$ 为节点之间与节点 $i$ 相连的邻居节点集合。对于无权图而言，$d_i$ 是节点 $v_i$ 的出度。

现在的目标是让条件概率$p_2(v_j|v_i)$尽可能的与经验分布${\hat{p}}_2(v_j|v_i)$相似：
$$O_2=-\sum _{i\in V}{\lambda }_{i}d({\hat{p}}_2(\cdot |v_i),p_2(\cdot |v_i))$$
其中，${\lambda }_i$ 是表示节点重要性的因子，可以通过预先计算节点的度数或者PageRank算法来得到。$d(\cdot ,\cdot )$ 用于度量两个分布之间的差距。

更具体的，假设 ${\lambda }_i=d_i$，使用忽略常数项的 KL 散度公式，则有：
$$O_2=-\sum _{(i,j)\in E}{w}_{ij}log(p_2(v_j|v_i))$$
对比一阶和二阶相度的概率函数，我们可以发现其实两者是非常相似的，只不过是二阶相似性每个节点有两个embedding，一个作为中心点的embeding和一个作为context时候的embeding。最终二阶使用的是作为中心点的embeding。实际使用的时候，对一阶近邻和二阶近邻分别训练，然后将两个向量拼接起来作为节点的向量表示。

优化技巧

负采样：

计算二阶相似度时，softmax 函数的分母计算需要遍历所有顶点，计算量太大了，论文采用了与 word2vec 论文类似的负采样优化的技巧，对边进行抽样生成负样本，每条边被抽中的概率为边的权重。于是，将每一条边$(i,j)$对应的目标函数变为：
$$log\sigma (u_j^{{}^{\prime }T}\cdot u_i)+\sum _{i=1}^K{E}_{v_n\sim P_n(v)}[log\sigma (-u_n^{{}^{\prime }T}\cdot u_i)]$$

其中，$\sigma$ 为sigmoid函数，K 为负样本的个数。负采样的好处在于：梯度下降的过程中只需要更新节点 $i,j$ 以及 K 个负采样的节点的向量即可。

以下是个人对公式的理解，不一定准确，如果有错还请指正：

感觉论文中的公式似乎表达的有点别扭，个人认为用下面的公式比较好理解：
$$O_2=log\sigma (u_j^{{}^{\prime }T}\cdot u_i)+\sum _{k=1}^K{E}_{v_k\sim P_n(v)}[log\sigma (-u_k^{{}^{\prime }T}\cdot u_i)]$$
其中$E_{v_k\sim P_n(v)}$ 表示取出 $v_k$ 的期望值，而$P_n(v)$ 表示采样时用的概率分布，可以是：
$$P_n(v)=\frac{(d_v{)}^{3/4}}{{\sum }_{j=1}^{|V|}(d_j{)}^{3/4}}$$
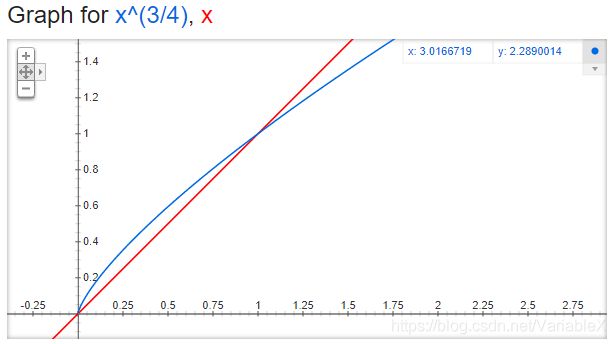
这个取 3/4 次幂的运算会产生一个效果，就是稍微增加低频节点的采样概率，降低高节点的采样概率。

可根据下图（google 的搜索栏中输入 “plot y = x^(3/4) and y = x” 可以快速画图）的对比看出来：

引入负采样后，最终得到的目标函数为：
$$O_2=-\sum _{(i,j)\in E}{w}_{ij}(log\sigma (u_j^{{}^{\prime }T}\cdot u_i)+\sum _{i=1}^K{E}_{v_n\sim P_n(v)}[log\sigma (-u_n^{{}^{\prime }T}\cdot u_i)])$$
边采样：

从上面的公式可以看到，每个样本都有一个权重 $w_{ij}$，有的样本w很高，有的样本w很低。在进行反向传播的时候，如果学习率过高，会导致w很大的样本梯度爆炸，如果学习率设置很小，会导致w很低的样本训练缓慢。为了解决这个问题，文中提出了边缘采样(Edge Sampling)的方法，将所有样本的系数都置为1，对图中的边重复采样来构造多个相同的正样本，采样率与权重 $w_{ij}$ 成正比。

扩充邻居：

对于一些顶点由于其邻接点非常少会导致embedding向量的学习不充分，论文提到可以利用邻居的邻居构造样本进行学习。为了解决这个问题，论文中提出了一个扩展邻居的办法，添加二阶邻居。所谓二阶邻居，就是从该节点到邻居节点之间存在两跳。

节点{1,2,3,4}就是节点7的二阶邻居，节点{8,9,10}就是节点6的二阶邻居。二阶邻居的权重计算方法如下：
$$w_{ij}=\sum _{k\in N(i)}{w}_{ik}\frac{w_{kj}}{d_k}$$

核心代码

这部分参考了浅梦的博客：【Graph Embedding】LINE：算法原理，实现和应用。

首先输入就是两个顶点的编号，然后分别拿到各自对应的embedding向量，最后输出内积的结果。 真实 label 定义为1或者-1。最终模型输出内积，然后可以对内积结果进行优化。

这里的实现中把1阶和2阶的方法融合到一起了，可以通过超参数order控制是分开优化还是联合优化，论文推荐分开优化。

# 损失函数
def line_loss(y_true, y_pred):
    return -K.mean(K.log(K.sigmoid(y_true*y_pred)))

# 构造模型
def create_model(numNodes, embedding_size, order='second'):

    v_i = Input(shape=(1,))
    v_j = Input(shape=(1,))

    first_emb = Embedding(numNodes, embedding_size, name='first_emb')
    second_emb = Embedding(numNodes, embedding_size, name='second_emb')
    context_emb = Embedding(numNodes, embedding_size, name='context_emb')

    # 一阶相似度
    v_i_emb = first_emb(v_i)
    v_j_emb = first_emb(v_j)

    # 二阶相似度
    v_i_emb_second = second_emb(v_i)
    v_j_context_emb = context_emb(v_j)
	# 节点 i,j 的内积
    first = Lambda(lambda x: tf.reduce_sum(
        x[0]*x[1], axis=-1, keep_dims=False), name='first_order')([v_i_emb, v_j_emb])
	# 节点 i 与 节点j上下文表示 的内积
    second = Lambda(lambda x: tf.reduce_sum(
        x[0]*x[1], axis=-1, keep_dims=False), name='second_order')([v_i_emb_second, v_j_context_emb])

    if order == 'first':
        output_list = [first]
    elif order == 'second':
        output_list = [second]
    else:
        output_list = [first, second]

    model = Model(inputs=[v_i, v_j], outputs=output_list)

参考文章：

Graph Embedding：从DeepWalk到SDNE - 知乎

Graph Embedding之探索LINE

推荐系统的中 Embedding 的应用实践 | 卢明冬的博客