CODEFORCES ROUND #645 (DIV. 2)
http://www.yyycode.cn/index.php/2020/05/30/codeforces-round-645-div-2/
A. Park Lightingtime
limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output
Due to the coronavirus pandemic, city authorities obligated citizens to keep a social distance. The mayor of the city Semyon wants to light up Gluharniki park so that people could see each other even at night to keep the social distance.
The park is a rectangular table with nn rows and mm columns, where the cells of the table are squares, and the boundaries between the cells are streets. External borders are also streets. Every street has length 11. For example, park with n=m=2n=m=2 has 1212 streets.
You were assigned to develop a plan for lighting the park. You can put lanterns in the middle of the streets. The lamp lights two squares near it (or only one square if it stands on the border of the park).
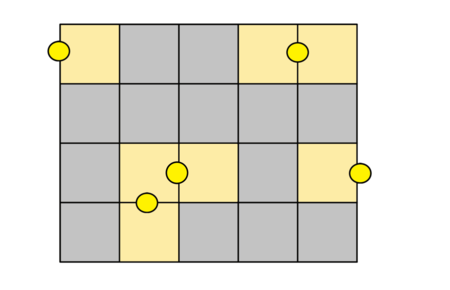
The park sizes are: n=4n=4, m=5m=5. The lighted squares are marked yellow. Please note that all streets have length 11. Lanterns are placed in the middle of the streets. In the picture not all the squares are lit.
Semyon wants to spend the least possible amount of money on lighting but also wants people throughout the park to keep a social distance. So he asks you to find the minimum number of lanterns that are required to light all the squares.Input
The first line contains a single integer tt (1≤t≤1041≤t≤104) — the number of test cases in the input. Then tt test cases follow.
Each test case is a line containing two integers nn, mm (1≤n,m≤1041≤n,m≤104) — park sizes.Output
Print tt answers to the test cases. Each answer must be a single integer — the minimum number of lanterns that are required to light all the squares.ExampleinputCopy
5 1 1 1 3 2 2 3 3 5 3
outputCopy
1 2 2 5 8
Note
Possible optimal arrangement of the lanterns for the 22-nd test case of input data example:
Possible optimal arrangement of the lanterns for the 33-rd test case of input data example:
题意:给一个n,m为边的矩形,问最少的灯使得整个矩形照亮
思路:又考了奇数偶数(话说奇偶性考得真的多
#include
#include
#include
#include
#include
using namespace std;
const int maxn=1e5;
typedef long long LL;
int main(void)
{
LL t;cin>>t;
while(t--)
{
LL n,m;cin>>n>>m;
if(n==1&&m==1) cout<<1< B. Maria Breaks the Self-isolation
Maria is the most active old lady in her house. She was tired of sitting at home. She decided to organize a ceremony against the coronavirus.
She has nn friends who are also grannies (Maria is not included in this number). The ii-th granny is ready to attend the ceremony, provided that at the time of her appearance in the courtyard there will be at least aiai other grannies there. Note that grannies can come into the courtyard at the same time. Formally, the granny ii agrees to come if the number of other grannies who came earlier or at the same time with her is greater than or equal to aiai.
Grannies gather in the courtyard like that.
- Initially, only Maria is in the courtyard (that is, the initial number of grannies in the courtyard is 11). All the remaining nn grannies are still sitting at home.
- On each step Maria selects a subset of grannies, none of whom have yet to enter the courtyard. She promises each of them that at the time of her appearance there will be at least aiai other grannies (including Maria) in the courtyard. Maria can call several grannies at once. In this case, the selected grannies will go out into the courtyard at the same moment of time.
- She cannot deceive grannies, that is, the situation when the ii-th granny in the moment of appearing in the courtyard, finds that now there are strictly less than aiai other grannies (except herself, but including Maria), is prohibited. Please note that if several grannies appeared in the yard at the same time, then each of them sees others at the time of appearance.
Your task is to find what maximum number of grannies (including herself) Maria can collect in the courtyard for the ceremony. After all, the more people in one place during quarantine, the more effective the ceremony!
Consider an example: if n=6n=6 and a=[1,5,4,5,1,9]a=[1,5,4,5,1,9], then:
- at the first step Maria can call grannies with numbers 11 and 55, each of them will see two grannies at the moment of going out into the yard (note that a1=1≤2a1=1≤2 and a5=1≤2a5=1≤2);
- at the second step, Maria can call grannies with numbers 22, 33 and 44, each of them will see five grannies at the moment of going out into the yard (note that a2=5≤5a2=5≤5, a3=4≤5a3=4≤5 and a4=5≤5a4=5≤5);
- the 66-th granny cannot be called into the yard — therefore, the answer is 66 (Maria herself and another 55 grannies).
Input
The first line contains a single integer tt (1≤t≤1041≤t≤104) — the number of test cases in the input. Then test cases follow.
The first line of a test case contains a single integer nn (1≤n≤1051≤n≤105) — the number of grannies (Maria is not included in this number).
The second line contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤2⋅1051≤ai≤2⋅105).
It is guaranteed that the sum of the values nn over all test cases of the input does not exceed 105105.Output
For each test case, print a single integer kk (1≤k≤n+11≤k≤n+1) — the maximum possible number of grannies in the courtyard.ExampleinputCopy
4 5 1 1 2 2 1 6 2 3 4 5 6 7 6 1 5 4 5 1 9 5 1 2 3 5 6
outputCopy
6 1 6 4
Note
In the first test case in the example, on the first step Maria can call all the grannies. Then each of them will see five grannies when they come out. Therefore, Maria and five other grannies will be in the yard.
In the second test case in the example, no one can be in the yard, so Maria will remain there alone.
The third test case in the example is described in the details above.
In the fourth test case in the example, on the first step Maria can call grannies with numbers 11, 22 and 33. If on the second step Maria calls 44 or 55 (one of them), then when a granny appears in the yard, she will see only four grannies (but it is forbidden). It means that Maria can’t call the 44-th granny or the 55-th granny separately (one of them). If she calls both: 44 and 55, then when they appear, they will see 4+1=54+1=5 grannies. Despite the fact that it is enough for the 44-th granny, the 55-th granny is not satisfied. So, Maria cannot call both the 44-th granny and the 55-th granny at the same time. That is, Maria and three grannies from the first step will be in the yard in total.
题意:每个人有一个聚会值,要求来了的人数(算同时来的)>=聚会值,问最多能拉到多少人
思路:和之前的cfdiv2一道分配人,每个人有经验值很像,那道题是sort后从前往后尺取,这道题sort就从后往前贪心
#include
#include
#include
#include
#include
using namespace std;
const int maxn=2e5+10;
typedef long long LL;
LL a[maxn];
int main(void)
{
LL t;cin>>t;
while(t--)
{
LL n;cin>>n;
for(LL i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+1+n);
if(a[n]<=n) cout<=1;i--)
{
if(a[i]<=i)
{
sum+=i;break;
}
}
cout< C. Celex Update
During the quarantine, Sicromoft has more free time to create the new functions in “Celex-2021”. The developers made a new function GAZ-GIZ, which infinitely fills an infinite table to the right and down from the upper left corner as follows:
The cell with coordinates (x,y)(x,y) is at the intersection of xx-th row and yy-th column. Upper left cell (1,1)(1,1) contains an integer 11.
The developers of the SUM function don’t sleep either. Because of the boredom, they teamed up with the developers of the RAND function, so they added the ability to calculate the sum on an arbitrary path from one cell to another, moving down or right. Formally, from the cell (x,y)(x,y) in one step you can move to the cell (x+1,y)(x+1,y) or (x,y+1)(x,y+1).
After another Dinwows update, Levian started to study “Celex-2021” (because he wants to be an accountant!). After filling in the table with the GAZ-GIZ function, he asked you to calculate the quantity of possible different amounts on the path from a given cell (x1,y1)(x1,y1) to another given cell (x2,y2(x2,y2), if you can only move one cell down or right.
Formally, consider all the paths from the cell (x1,y1)(x1,y1) to cell (x2,y2)(x2,y2) such that each next cell in the path is located either to the down or to the right of the previous one. Calculate the number of different sums of elements for all such paths.Input
The first line contains one integer tt (1≤t≤571791≤t≤57179) — the number of test cases.
Each of the following tt lines contains four natural numbers x1x1, y1y1, x2x2, y2y2 (1≤x1≤x2≤1091≤x1≤x2≤109, 1≤y1≤y2≤1091≤y1≤y2≤109) — coordinates of the start and the end cells.Output
For each test case, in a separate line, print the number of possible different sums on the way from the start cell to the end cell.ExampleinputCopy
4 1 1 2 2 1 2 2 4 179 1 179 100000 5 7 5 7
outputCopy
2 3 1 1
Note
In the first test case there are two possible sums: 1+2+5=81+2+5=8 and 1+3+5=91+3+5=9.
题意:求(a,b)–>(c,d)的所有路径总数中有多少路径和不同的。
思路:当时自己是观察规律的。赛后讨论想出了证明
观察发现,右上的数字比左下的小。那么可以看到最大的一条路在要求的矩阵中是L形的,最小的一条路是对称过去的反L 形的。
那么我们要求的就转化成了求 路的权值最大-路的权值最小的+1是多少。(中间的某个和是都能走出来的)
那么对一个矩形来说,观察最大和最小的和两条路。
找最大路径和最小路径每一步的差,得出式子是 0(起点)+1+2+3+….x-1+x+x+x..+x-1+x-2+….3+2+1+0(终点);
对于1+2+3+..+x-1有两个,求和得x*(x-1);
x有 (x+y+1)-x*2个。
最后得出 x*(y-x+1)+x*(x-1)==yx,所以一共有yx+1;
#include
#include
#include
#include
#include
using namespace std;
const int maxn=1e5;
typedef long long LL;
int main(void)
{
LL t;cin>>t;
while(t--)
{
LL x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
cout<<(x2-x1)*(y2-y1)+1< D. The Best Vacation
You’ve been in love with Coronavirus-chan for a long time, but you didn’t know where she lived until now. And just now you found out that she lives in a faraway place called Naha.
You immediately decided to take a vacation and visit Coronavirus-chan. Your vacation lasts exactly xx days and that’s the exact number of days you will spend visiting your friend. You will spend exactly xx consecutive (successive) days visiting Coronavirus-chan.
They use a very unusual calendar in Naha: there are nn months in a year, ii-th month lasts exactly didi days. Days in the ii-th month are numbered from 11 to didi. There are no leap years in Naha.
The mood of Coronavirus-chan (and, accordingly, her desire to hug you) depends on the number of the day in a month. In particular, you get jj hugs if you visit Coronavirus-chan on the jj-th day of the month.
You know about this feature of your friend and want to plan your trip to get as many hugs as possible (and then maybe you can win the heart of Coronavirus-chan).
Please note that your trip should not necessarily begin and end in the same year.Input
The first line of input contains two integers nn and xx (1≤n≤2⋅1051≤n≤2⋅105) — the number of months in the year and the number of days you can spend with your friend.
The second line contains nn integers d1,d2,…,dnd1,d2,…,dn, didi is the number of days in the ii-th month (1≤di≤1061≤di≤106).
It is guaranteed that 1≤x≤d1+d2+…+dn1≤x≤d1+d2+…+dn.Output
Print one integer — the maximum number of hugs that you can get from Coronavirus-chan during the best vacation in your life.ExamplesinputCopy
3 2 1 3 1
outputCopy
5
inputCopy
3 6 3 3 3
outputCopy
12
inputCopy
5 6 4 2 3 1 3
outputCopy
15
Note
In the first test case, the numbers of the days in a year are (indices of days in a corresponding month) {1,1,2,3,1}{1,1,2,3,1}. Coronavirus-chan will hug you the most if you come on the third day of the year: 2+3=52+3=5 hugs.
In the second test case, the numbers of the days are {1,2,3,1,2,3,1,2,3}{1,2,3,1,2,3,1,2,3}. You will get the most hugs if you arrive on the third day of the year: 3+1+2+3+1+2=123+1+2+3+1+2=12 hugs.
In the third test case, the numbers of the days are {1,2,3,4,1,2,1,2,3,1,1,2,3}{1,2,3,4,1,2,1,2,3,1,1,2,3}. You will get the most hugs if you come on the twelfth day of the year: your friend will hug you 2+3+1+2+3+4=152+3+1+2+3+4=15 times.
题意:每个月有d[i]天,有x天度假,要求连续,可以跨年,保证度假日子小于一整年。求d[i]求和最大的一段
思路:贪心+前缀和+二分
贪心:
有这么一段区间,贪A和贪B。
当bn(月的最后一天)>an-2,明显可以得出B是最优的。
那么当bn
所以贪心把末尾的一天放到月末。
然后我们利用前缀和统计每个月的天数和价值。然后枚举右端点,二分左端点,找到
sum[i]-sum[l]>x;且sum[i]-sum[l+1]<=x
那么价值为summoney[i]-summoney[l+1];再算多出的x部分–知道x多出有多少天,然后在多出的区间里用等差数列公式算出来。比如多出3天,就是那段区间的后三天的价值和。
#include
#include
#include
#include
#include
using namespace std;
const int maxn=4e5+20;
typedef long long LL;
LL a[maxn];
LL sumday[maxn];
LL summoney[maxn];
int main(void)
{
LL n,x;cin>>n>>x;
for(LL i=1;i<=n;i++)
{
cin>>a[i];
sumday[i]=sumday[i-1]+a[i];
summoney[i]=summoney[i-1]+(1+a[i])*a[i]/2;
}
for(LL i=n+1;i<=2*n;i++)
{
a[i]=a[i-n];
sumday[i]=sumday[i-1]+a[i];
summoney[i]=summoney[i-1]+(1+a[i])*a[i]/2;
}
LL res=0;
for(LL i=1;i<=2*n;i++)
{
LL l=0;LL r=i+1;
//边界处理
//找出第一个区间差大于等于x的位置
while(l>1;
if(sumday[i]-sumday[mid]<=x) r=mid;
else l=mid+1;
}
if(l==0||r==i+1) continue;
LL resday=x-(sumday[i]-sumday[l]);
LL sum=summoney[i]-summoney[l];
if(a[l]>=resday) sum+=(2*a[l]-resday+1)*resday/2;
res=max(res,sum);
}
cout<