RL 实践（6）—— CartPole【REINFORCE with baseline & A2C】

• 本文介绍 REINFORCE with baseline 和 A2C 这两个带 baseline 的策略梯度方法，并在 CartPole-V0 上验证它们和无 baseline 的原始方法 REINFORCE & Actor-Critic 的优势
• 参考：《动手学强化学习》
• 完整代码下载：7_[Gym] CartPole-V0 (REINFORCE with baseline and A2C)

---

1. CartPole-V0 环境

• 本次实验使用 gym 自带的 CartPole-V0 环境。这是一个经典的一阶倒立摆控制问题，agent 的任务是通过左右移动保持车上的杆竖直，若杆的倾斜度数过大，或者车子离初始位置左右的偏离程度过大，或者坚持时间到达 200 帧，则游戏结束
  

• 此环境的状态空间为

  维度	意义	取值范围
  0	滚球 x 轴坐标	$[0,\text{width}]$
  1	滚球 y 轴坐标	$[-\inf ,\inf ]$
  2	滚球 x 轴速度	$[-41.8°,41.8°]$
  3	滚球 y 轴速度	$[-\inf ,\inf ]$

  动作空间为

  维度	意义
  0	向左移动小车
  1	向右移动小车

  奖励函数为每个 timestep 得到 1 的奖励，agent 坚持时间越长，则最后的分数越高，坚持 200 帧即可获得最高的分数 200

  倒立摆问题传统上可以用 pid 方法良好地解决。如果对 PID 这一套感兴趣，可以参考我的视频

  • 一看就懂的pid控制理论入门
  • 倒立摆模拟器

• 下面给出环境的测试代码

  import os
  import sys
  import gym
  base_path = os.path.abspath(os.path.join(os.path.dirname(__file__), '..'))
  sys.path.append(base_path)
  
  import time
  from gym.utils.env_checker import check_env
  
  env_name = 'CartPole-v0'
  env = gym.make(env_name, render_mode='human')
  check_env(env.unwrapped)    # 检查环境是否符合 gym 规范
  env.action_space.seed(10)
  observation, _ = env.reset(seed=10)
  
  # 测试环境
  for i in range(100):
      while True:
          action = env.action_space.sample()
          state, reward, terminated, truncated, _ = env.step(action)
  
          if terminated or truncated:
              env.reset()
              break
  
          time.sleep(0.01)
          env.render()
  
  # 关闭环境渲染
  env.close()
  

2. Policy Gradient with Baseline

• 上文 RL 实践（5）—— 二维滚球环境【REINFORCE & Actor-Critic】 介绍了两种经典的 Policy-Gradient 方法，Actor-Critic 和 REINFORCE，本文介绍这两种方法通用的一个改进技巧，可以有效提高算法的性能，并减小方差。
• 首先回顾一下策略梯度方法的基本原理：对于用参数 $\theta$ 形式化的策略网络 ${\pi }_{\theta }:\mathcal{S}\to \mathcal{A}$，策略学习可以转换为如下优化问题
  $$\underset{\theta }{\max }\left\{J(\theta )\stackrel{△}{=}{\mathbb{E}}_s[V_{{\pi }_{\theta }}(s)]\right\}$$ 这个优化问题可以用梯度上升来解
  $$\theta \leftarrow \theta +\beta \cdot {▽}_{\theta }J(\theta )$$ 其中策略梯度可以用策略梯度定理计算
  $${▽}_{\theta }J(\theta )\propto {\mathbb{E}}_{S\sim d(\cdot )}\left[{\mathbb{E}}_{A\sim {\pi }_{\theta }(\cdot \mid S)}\left[{▽}_{\theta }\ln {\pi }_{\theta }(A\mid S)\cdot Q_{{\pi }_{\theta }}(S,A)\right]\right]$$ 我们通过两次 MC 近似消去两个积分，得到随机策略梯度
  $$g_{\theta }(s,a)\stackrel{△}{=}{▽}_{\theta }\ln {\pi }_{\theta }(a|s)\cdot Q_{{\pi }_{\theta }}(s,a)$$ 其中 $s,a$ 来自策略 ${\pi }_{\theta }$ 和环境环境的某个具体 transition。最后，对动作价值函数 $Q_{\pi }(s,a)$ 的两种近似方案引出了两种策略梯度方法：
  1. REINFORCE：用实际 return $u$ MC 近似 $Q_{\pi }(s,a)$
  2. Actor-Critic：用神经网络（Critic） $q_w(s,a)$ 近似 $Q_{\pi }(s,a)$

2.1 带 baseline 的策略梯度定理

• 我们首先证明一个引理：设 $b$ 是任意函数，$b$ 不依赖于 $A$。那么对于任意的 $s$，有
  $${\mathbb{E}}_{A\sim {\pi }_{\mathbf{\theta }}(\cdot \mid s)}\left[b\cdot {▽}_{\theta }\ln {\pi }_{\theta }(A\mid s)\right]=0$$

  由于 $b$ 不依赖于动作 $A$，首先把 $b$ 提取到期望外面
  $$\begin{array}{rl}{\mathbb{E}}_{A\sim \pi (\cdot \mid s;\mathbf{\theta })}\left[b\cdot \frac{\partial \ln \pi (A\mid s;\mathbf{\theta })}{\partial \mathbf{\theta }}\right]& =b\cdot {\mathbb{E}}_{A\sim \pi (\cdot \mid s;\mathbf{\theta })}\left[\frac{\partial \ln \pi (A\mid s;\mathbf{\theta })}{\partial \mathbf{\theta }}\right]\\ & =b\cdot \sum _{a\in \mathcal{A}}\pi (a\mid s;\mathbf{\theta })\cdot \frac{\partial \ln \pi (a\mid s;\mathbf{\theta })}{\partial \mathbf{\theta }}\\ & =b\cdot \sum _{a\in \mathcal{A}}\pi (a\mid s;\mathbf{\theta })\cdot \frac{1}{\pi (a\mid s;\mathbf{\theta })}\cdot \frac{\partial \pi (a\mid s;\mathbf{\theta })}{\partial \mathbf{\theta }}\\ & =b\cdot \sum _{a\in \mathcal{A}}\frac{\partial \pi (a\mid s;\mathbf{\theta })}{\partial \mathbf{\theta }}\end{array}$$ 上式最右边的连加是关于 $a$ 求的，而偏导是关于 $\theta$ 求的，因此可以把连加放入偏导内部
  $$\begin{array}{rl}{\mathbb{E}}_{A\sim \pi (\cdot \mid s;\mathbf{\theta })}\left[b\cdot \frac{\partial \ln \pi (A\mid s;\mathbf{\theta })}{\partial \mathbf{\theta }}\right]& =b\cdot \frac{\partial }{\partial \mathbf{\theta }}\underset{\text{恒等于 }1}{\sum _{a\in \mathcal{A}}\pi (a\mid s;\mathbf{\theta })}.\\ & =b\cdot \frac{\partial 1}{\partial \mathbf{\theta }}=0.\end{array}$$

• 证明此引理后，我们可以把这一项引入到策略梯度定义给出的策略梯度中
  $$\begin{array}{rl}{▽}_{\theta }J(\theta )& \propto {\mathbb{E}}_{S\sim d(\cdot )}\left[{\mathbb{E}}_{A\sim {\pi }_{\theta }(\cdot \mid S)}\left[{▽}_{\theta }\ln {\pi }_{\theta }(A\mid S)\cdot Q_{{\pi }_{\theta }}(S,A)\right]\right]\\ & ={\mathbb{E}}_{S\sim d(\cdot )}[{\mathbb{E}}_{A\sim {\pi }_{\theta }(\cdot \mid S)}\left[{▽}_{\theta }\ln {\pi }_{\theta }(A\mid S)\cdot Q_{{\pi }_{\theta }}(S,A)\right]-0]\\ & ={\mathbb{E}}_{S\sim d(\cdot )}[{\mathbb{E}}_{A\sim {\pi }_{\theta }(\cdot \mid S)}\left[{▽}_{\theta }\ln {\pi }_{\theta }(A\mid S)\cdot Q_{{\pi }_{\theta }}(S,A)\right]-{\mathbb{E}}_{A\sim {\pi }_{\mathbf{\theta }}(\cdot \mid s)}\left[b\cdot {▽}_{\theta }\ln {\pi }_{\theta }(A\mid s)\right]]\\ & ={\mathbb{E}}_{S\sim d(\cdot )}\left[{\mathbb{E}}_{A\sim {\pi }_{\theta }(\cdot \mid S)}\left[{▽}_{\theta }\ln {\pi }_{\theta }(A\mid S)\cdot (Q_{{\pi }_{\theta }}(S,A)-b)\right]\right]\end{array}$$ 进而可以得到 带基线的随机策略梯度，它仍是对原策略梯度的无偏估计
  $$g_{\theta }(s,a;b)\stackrel{△}{=}{▽}_{\theta }\ln {\pi }_{\theta }(a|s)\cdot [Q_{{\pi }_{\theta }}(s,a)-b]$$ 其中不依赖于 $A$ 的任意函数 $b$ 就是所谓的 基线(baseline)，它的引入不会影响策略梯度（期望不变），但会影响随机策略梯度 $g_{\theta }(s,a;b)$，进而影响随机策略梯度的方差
  $$\mathrm{Var}={\mathbb{E}}_{S,A}\left[{\Vert g_{\theta }(s,a;b)-{\nabla }_{\mathbf{\theta }}J(\mathbf{\theta })\Vert }^2\right]$$ 如果 $b$ 很接近 $Q_{{\pi }_{\theta }}(s,a;b)$ 关于 $a$ 的均值，那么方差会比较小。因此 $b=V_{{\pi }_{\theta }}(s)$ 是很好的基线

2.2 REINFORCE with baseline

• 我们使用 2.1 节得到的带基线的随机策略梯度 $g_{\theta }(s,a;b)$ 改写前文的 REINFORCR 算法，基线设置为 $b=V_{{\pi }_{\theta }}(s)$，即
  $$g_{\theta }(s,a)\stackrel{△}{=}{▽}_{\theta }\ln {\pi }_{\theta }(a|s)\cdot [Q_{{\pi }_{\theta }}(s,a)-V_{{\pi }_{\theta }}(s)]$$ 其中 $Q_{{\pi }_{\theta }}(s,a)$ 仍然和 REINFORCR 一样使用轨迹的真实 return $u$ 来估计，$V_{{\pi }_{\theta }}(s)$ 则引入一个价值网络 $v_{\omega }$ 来估计，估计方式为 MC（而非 TD bootstrap）

2.2.1 伪代码

• 每轮迭代我们用当前策略 ${\pi }_{\theta }$ 交互得到一条轨迹，然后计算出每一个 transition $(s,a,r,s^{\prime })$ 对应的 return $u$，首先用 $u$ 作为标签用 mse loss 优化价值网络 $v_{\omega }$（这样价值网络可以更好地估计 $V_{{\pi }_{\theta }}$），然后利用更新后的 $v_w$ 计算 $g_{\theta }(s,a)$ 来更新策略网络 ${\pi }_{\theta }$。伪代码如下
  $$\begin{array}{rl}& 初始化策略网络{\pi }_{\theta }和价值网络v_{\omega }\\ & forepisodee=1\to Edo:\\ & 用当前策略{\pi }_{\theta }交互一条轨迹s_1,a_1,r_1,...,s_n,a_n,r_n\\ & 计算所有return{u}_t=\sum _{k=t}^m{\gamma }^{k-t}{r}_k,t=1,2,...,n\\ & 更新v_{\omega }参数l_{\omega }=\frac{1}{2n}\sum _{t=1}^n[v_{\omega }(s_t)-u_t{]}^2\\ & 更新{\pi }_{\theta }参数\theta \leftarrow \theta +\beta \cdot {▽}_{\theta }\ln {\pi }_{\theta }(a_t|s_t)\cdot (u_t-v_{\omega }(s_t)),t=1,2,...,n\\ & endfor\end{array}$$

2.2.2 用 REINFORCE with baseline 方法解决 CartPole 问题

• 定义策略网络和价值网络

  class PolicyNet(torch.nn.Module):
      ''' 策略网络是一个两层 MLP '''
      def __init__(self, input_dim, hidden_dim, output_dim):
          super(PolicyNet, self).__init__()
          self.fc1 = torch.nn.Linear(input_dim, hidden_dim)
          self.fc2 = torch.nn.Linear(hidden_dim, output_dim)
  
      def forward(self, x):
          x = F.relu(self.fc1(x))             # (1, hidden_dim)
          x = F.softmax(self.fc2(x), dim=1)   # (1, output_dim)
          return x
  
  class VNet(torch.nn.Module):
      ''' 价值网络是一个两层 MLP '''
      def __init__(self, input_dim, hidden_dim):
          super(VNet, self).__init__()
          self.fc1 = torch.nn.Linear(input_dim, hidden_dim)
          self.fc2 = torch.nn.Linear(hidden_dim, 1)
  
      def forward(self, x):
          x = F.relu(self.fc1(x))
          x = self.fc2(x)
          return
  

• 定义 REINFORCE with baseline agent

  class REINFORCE_Baseline(torch.nn.Module):
      def __init__(self, state_dim, hidden_dim, action_range, lr_policy, lr_value, gamma, device):
          super().__init__()
          self.policy_net = PolicyNet(state_dim, hidden_dim, action_range).to(device)
          self.v_net = VNet(state_dim, hidden_dim).to(device)
          self.optimizer_policy = torch.optim.Adam(self.policy_net.parameters(), lr=lr_policy)    # 使用Adam优化器
          self.optimizer_value = torch.optim.Adam(self.v_net.parameters(), lr=lr_value)           # 使用Adam优化器
          self.gamma = gamma
          self.device = device
  
      def take_action(self, state):  
          # 根据动作概率分布随机采样
          state = torch.tensor(state, dtype=torch.float).to(self.device)
          state = state.unsqueeze(0)
          probs = self.policy_net(state).squeeze()
          action_dist = torch.distributions.Categorical(probs)
          action = action_dist.sample()
          return action.item()
  
      def update(self, transition_dict):
          G, returns = 0, []
          for reward in reversed(transition_dict['rewards']):
              G = self.gamma * G + reward
              returns.insert(0, G)
  
          rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device).squeeze()     # (bsz, )
          returns = torch.tensor(returns, dtype=torch.float).view(-1, 1).to(self.device).squeeze()                        # (bsz, )
          states = torch.tensor(np.array(transition_dict['states']), dtype=torch.float).to(self.device)                   # (bsz, state_dim)
          actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)                                  # (bsz, action_dim)
  
          # 梯度清零
          self.optimizer_value.zero_grad()
          self.optimizer_policy.zero_grad()
          
          # 更新价值网络
          value_predicts = self.v_net(states).squeeze()                   # (bsz, )
          value_loss = torch.mean(F.mse_loss(value_predicts, returns))     
          value_loss.backward()
          self.optimizer_value.step()
  
          # 更新策略网络, 从轨迹最后一步起往前计算 return，每步回传累计梯度 
          for i in reversed(range(len(rewards))):
              action = actions[i]
              state = states[i]
              value = self.v_net(state).squeeze()                         # 使用更新过的价值网络预测价值
              G = returns[i]                                              # (state_dim, )
              probs = self.policy_net(state.unsqueeze(0)).squeeze()       # (action_range, )
              log_prob = torch.log(probs[action])
              policy_loss = -log_prob * (G - value.detach())              # value 是 v_net 给出的，将其 detach 以确保只更新 policy 参数
              policy_loss.backward()        
          self.optimizer_policy.step()    
  

• 进行训练并绘制性能曲线

  if __name__ == "__main__":
      def moving_average(a, window_size):
          ''' 生成序列 a 的滑动平均序列 '''
          cumulative_sum = np.cumsum(np.insert(a, 0, 0)) 
          middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
          r = np.arange(1, window_size-1, 2)
          begin = np.cumsum(a[:window_size-1])[::2] / r
          end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
          return np.concatenate((begin, middle, end))
  
      def set_seed(env, seed=42):
          ''' 设置随机种子 '''
          env.action_space.seed(seed)
          env.reset(seed=seed)
          random.seed(seed)
          np.random.seed(seed)
          torch.manual_seed(seed)
  
      state_dim = 4                               # 环境观测维度
      action_range = 2                            # 环境动作空间大小
      lr_policy = 2e-3
      lr_value = 3e-3
      num_episodes = 500
      hidden_dim = 64
      gamma = 0.98
      device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
  
      # build environment
      env_name = 'CartPole-v0'
      env = gym.make(env_name, render_mode='rgb_array')
      check_env(env.unwrapped)    # 检查环境是否符合 gym 规范
      set_seed(env, 42)
  
      # build agent
      agent = REINFORCE_Baseline(state_dim, hidden_dim, action_range, lr_policy, lr_value, gamma, device)
  
      # start training
      return_list = []
      for i in range(10):
          with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
              for i_episode in range(int(num_episodes / 10)):
                  episode_return = 0
                  transition_dict = {
                      'states': [],
                      'actions': [],
                      'next_states': [],
                      'rewards': [],
                      'dones': []
                  }
                  state, _ = env.reset()
  
                  # 以当前策略交互得到一条轨迹
                  while True:
                      action = agent.take_action(state)
                      next_state, reward, terminated, truncated, _ = env.step(action)
                      transition_dict['states'].append(state)
                      transition_dict['actions'].append(action)
                      transition_dict['next_states'].append(next_state)
                      transition_dict['rewards'].append(reward)
                      transition_dict['dones'].append(terminated or truncated)
                      state = next_state
                      episode_return += reward
                      
                      if terminated or truncated:
                          env.render()
                          break
                      #env.render()
  
                  # 用当前策略收集的数据进行 on-policy 更新
                  agent.update(transition_dict)
  
                  # 更新进度条
                  return_list.append(episode_return)
                  pbar.set_postfix({
                      'episode':
                      '%d' % (num_episodes / 10 * i + i_episode + 1),
                      'return':
                      '%.3f' % episode_return,
                      'ave return':
                      '%.3f' % np.mean(return_list[-10:])
                  })
                  pbar.update(1)
  
      # show policy performence
      mv_return_list = moving_average(return_list, 29)
      episodes_list = list(range(len(return_list)))
      plt.figure(figsize=(12,8))
      plt.plot(episodes_list, return_list, label='raw', alpha=0.5)
      plt.plot(episodes_list, mv_return_list, label='moving ave')
      plt.xlabel('Episodes')
      plt.ylabel('Returns')
      plt.title(f'{agent._get_name()} on CartPole-V0')
      plt.legend()
      plt.savefig(f'./result/{agent._get_name()}.png')
      plt.show()         
  

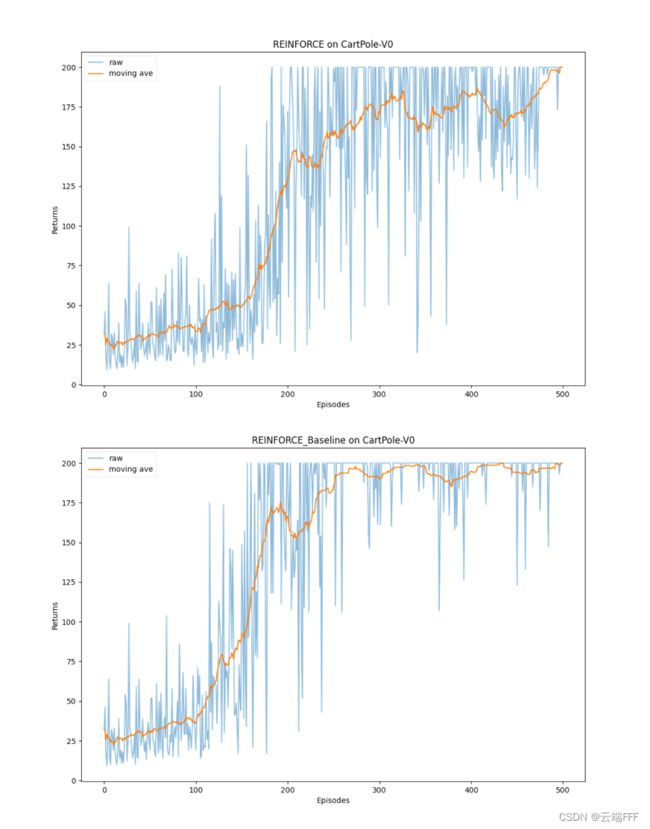
2.2.3 性能

• 对比前文介绍的普通 REINFORCE 方法和以上 REINFORCE with baseline 方法的性能曲线，如下
  
  可见引入 baseline 有效降低了方差，且加快了收敛速度

2.3 Advantage Actor-Critic (A2C)

• 我们使用 2.1 节得到的带基线的随机策略梯度 $g_{\theta }(s,a;b)$ 改写前文的 REINFORCR 算法，基线设置为 $b=V_{{\pi }_{\theta }}(s)$，即
  $$g_{\theta }(s,a)\stackrel{△}{=}{▽}_{\theta }\ln {\pi }_{\theta }(a|s)\cdot [Q_{{\pi }_{\theta }}(s,a)-V_{{\pi }_{\theta }}(s)]$$ 其中 $Q_{{\pi }_{\theta }}(s,a)-V_{{\pi }_{\theta }}(s)$ 被称作优势函数 (advantage function)，因此基于上面公式得到的 actor-critic 方法被称为 advantage actor-critic (A2C)。A2C 属于 actor-critic 方法，有一个策略网络 ${\pi }_{\theta }$ 作为 Actor 用于控制 agent 运动，还有一个价值网络 $v_{\omega }$ 作为 Critic，他的评分可以帮助 Actor 改进。两个神经网络的结构与上一节中的完全相同，但是本节和上一节用不同的方法训练两个神经网络

2.3.1 伪代码

• 这里训练价值网络时不像 REINFORCE with baseline 那样直接优化 mse loss 去靠近真实 return（MC），而是用 mse loss 去优化 Sarsa TD error。具体而言，给定 transition $(s,a,r,s^{\prime })$，如下得到 TD error 的 mse loss
  $$l_{\omega }=\frac{1}{2}[v_{\omega }(s)-(r+v_{\omega }(s^{\prime })){]}^2$$
• 训练策略网络时利用 Bellman 公式得到 $Q$ 和 $V$ 的关系
  $$Q_{\pi }\left(s_t,a_t\right)={\mathbb{E}}_{S_{t+1}\sim p(\cdot |s_t,a_t)}[R_t+\gamma V_{\pi }(S_{t+1})]$$ 把带基线的随机策略梯度中的 $Q_{{\pi }_{\theta }}(s,a)$ 进行替换
  $$\begin{array}{rl}{\mathbf{g}}_{\theta }\left(s,a\right)& ={▽}_{\theta }\ln {\pi }_{\theta }(a|s)\cdot [Q_{{\pi }_{\theta }}(s,a)-V_{{\pi }_{\theta }}(s)]\\ & ={▽}_{\theta }\ln {\pi }_{\theta }(a|s)\cdot [{\mathbb{E}}_{S_{t+1}}\left[R_t+\gamma V_{{\pi }_{\theta }}\left(S_{t+1}\right)\right]-V_{{\pi }_{\theta }}(s)]\end{array}$$ 使用真实的 transition $(s,a,r,s^{\prime })$ 进行 MC 近似，得到随机策略梯度
  $${\tilde{\mathbf{g}}}_{\theta }\left(s,a\right)\triangleq [\underset{\mathrm{TD}\text{ Error}}{r+\gamma \cdot v_{\omega }\left(s^{\prime }\right)-v_{\omega }\left(s\right)}]\cdot {\nabla }_{\mathbf{\theta }}\ln {\pi }_{\theta }\left(a\mid s\right).$$ 用这个随机策略梯度做梯度上升即可优化策略网络
• A2C 的伪代码如下
  $$\begin{array}{rl}& 初始化策略网络{\pi }_{\theta }和价值网络v_{\omega }\\ & forepisodee=1\to Edo:\\ & 用当前策略{\pi }_{\theta }交互一条轨迹s_1,a_1,r_1,...,s_n,a_n,r_n\\ & 计算所有\text{TD erro}r{\delta }_t=r_t+\gamma \cdot v_{\omega }\left(s_{t+1}\right)-v_{\omega }\left(s_t\right)\\ & 更新v_{\omega }参数l_{\omega }=\frac{1}{2n}\sum _{t=1}^n[{\delta }_t{]}^2\\ & 更新{\pi }_{\theta }参数\theta \leftarrow \theta +\beta \cdot {▽}_{\theta }\ln {\pi }_{\theta }(a_t|s_t)\cdot {\delta }_t,t=1,2,...,n\\ & endfor\end{array}$$

2.3.2 用 A2C 方法解决 CartPole 问题

• 只需要重新定义 A2C agent，其他代码全部和 REINFORCE with baseline 一致

  class A2C(torch.nn.Module):
      def __init__(self, state_dim, hidden_dim, action_range, actor_lr, critic_lr, gamma, device):
          super().__init__()
          self.gamma = gamma
          self.device = device
          
          self.actor = PolicyNet(state_dim, hidden_dim, action_range).to(device)
          self.critic = VNet(state_dim, hidden_dim).to(device) 
          self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
          self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
          
      def take_action(self, state):
          state = torch.tensor(state, dtype=torch.float).to(self.device)
          state = state.unsqueeze(0)
          probs = self.actor(state)
          action_dist = torch.distributions.Categorical(probs)
          action = action_dist.sample()
          return action.item()
  
      def update(self, transition_dict):
          states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
          actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
          rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
          next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
          dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
  
          # Cirtic loss 
          td_target = rewards + self.gamma * self.critic(next_states) * (1-dones)
          critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
  
          # Actor loss 
          td_error = td_target - self.critic(states)  
          probs = self.actor(states).gather(1, actions)
          log_probs = torch.log(probs)
          actor_loss = torch.mean(-log_probs * td_error.detach())
  
          # 更新网络参数
          self.actor_optimizer.zero_grad()
          self.critic_optimizer.zero_grad()
          actor_loss.backward()           
          critic_loss.backward()      
          self.actor_optimizer.step()     
          self.critic_optimizer.step()    
  

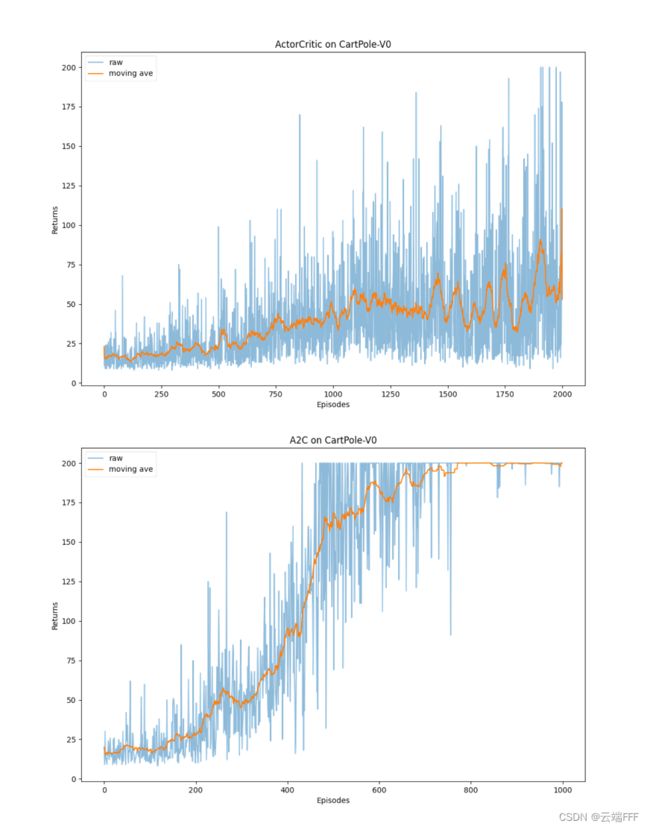
2.3.3 性能

• 对比前文介绍的普通 Actor-Critic 方法和以上 A2C 方法的性能曲线，如下
  
  可见普通 Actor-Critic 方法即使交互轨迹数量翻倍也难以收敛，而 A2C 收敛迅速，性能稳定

2.3.4 引入目标网络

• 之前我们讲 DQN 时提到过关于 bootstrap 迭代的一个问题

  TD bootstrap 是在使用由 DQN 生成的优化目标 TD target 来优化 DQN 网络。这就导致优化目标随着训练进行不断变化，违背了监督学习的 i.i.d 原则，导致训练不稳定

  A2C 中的 critic 网络同样具有此问题，为了稳定训练，我们可以像 DQN 那样引入一个参数更新频率更低的目标网络来稳定 TD target，从而稳定训练过程。考虑到 A2C 本身是 on-policy 方法，这里不适合像 DQN 那样按照一定周期去替换目标网络参数，而是应该使用加权平均的方式来更新。设引入目标网络 $v_{w^{\prime }}$ 和更新权重 $\tau$，A2C 算法的伪代码变为
  $$\begin{array}{rl}& 初始化策略网络{\pi }_{\theta },价值网络v_{\omega }和目标网络v_{{\omega }^{\prime }}\\ & forepisodee=1\to Edo:\\ & 用当前策略{\pi }_{\theta }交互一条轨迹s_1,a_1,r_1,...,s_n,a_n,r_n\\ & 计算所有\text{TD erro}r{\delta }_t=r_t+\gamma \cdot v_{{\omega }^{\prime }}\left(s_{t+1}\right)-v_{\omega }\left(s_t\right)\\ & 更新v_{\omega }参数l_{\omega }=\frac{1}{2n}\sum _{t=1}^n[{\delta }_t{]}^2\\ & 更新v_{{\omega }^{\prime }}参数{\omega }^{\prime }\leftarrow \tau w^{\prime }+(1-\tau )w\\ & 更新{\pi }_{\theta }参数\theta \leftarrow \theta +\beta \cdot {▽}_{\theta }\ln {\pi }_{\theta }(a_t|s_t)\cdot {\delta }_t,t=1,2,...,n\\ & endfor\end{array}$$

• 带目标网络的的 A2C agent 实现如下，其他代码基本和 A2C 一致

  class A2C_Target(torch.nn.Module):
      def __init__(self, state_dim, hidden_dim, action_range, target_weight, actor_lr, critic_lr, gamma, device):
          super().__init__()
          self.gamma = gamma
          self.device = device
          self.target_weight = target_weight 
  
          self.actor = PolicyNet(state_dim, hidden_dim, action_range).to(device)
          self.critic = VNet(state_dim, hidden_dim).to(device) 
          self.target = VNet(state_dim, hidden_dim).to(device) 
          self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
          self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
          
      def take_action(self, state):
          state = torch.tensor(state, dtype=torch.float).to(self.device)
          state = state.unsqueeze(0)
          probs = self.actor(state)
          action_dist = torch.distributions.Categorical(probs)
          action = action_dist.sample()
          return action.item()
  
      def update(self, transition_dict):
          states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
          actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
          rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
          next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
          dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
  
          # Cirtic loss 
          td_target = rewards + self.gamma * self.target(next_states) * (1-dones)
          critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
  
          # Actor loss 
          td_error = td_target - self.critic(states)  
          probs = self.actor(states).gather(1, actions)
          log_probs = torch.log(probs)
          actor_loss = torch.mean(-log_probs * td_error.detach())
  
          # 更新网络参数
          self.actor_optimizer.zero_grad()
          self.critic_optimizer.zero_grad()
          actor_loss.backward()           
          critic_loss.backward()      
          self.actor_optimizer.step()     
          self.critic_optimizer.step()    
  
          # 更新 target 网络参数为 target 和 critic 的加权平均
          w = self.target_weight  
          params_target = list(self.target.parameters())
          params_critic = list(self.critic.parameters())
  
          for i in range(len(params_target)):
              new_param = w * params_target[i] + (1 - w) * params_critic[i]
              params_target[i].data.copy_(new_param)
  

• 当 $\tau =0.95$ 时性能较好，和 A2C 相比如下
  
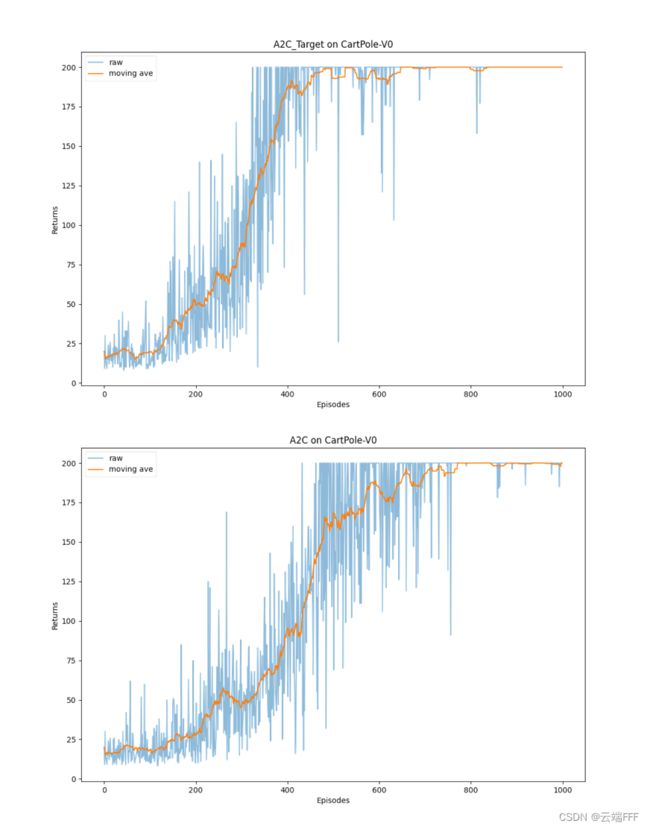
  可见引入目标网络后收敛更快，收敛后也更稳定

3. 总结

• 在策略梯度中加入基线 (baseline) 可以降低方差，显著提升实验效果。实践中常用 $b=V_{\pi }(s)$ 作为 baseline。
  • 可以用基线来改进 REINFORCE 算法。这时我们仍然用真实 return 来估计策略梯度中的 $Q$ 价值，并引入价值网络 $v_w$，使用 MC 方法来估计状态价值函数 $V_{\pi }(s)$ 作为 baseline。如此计算出随机策略梯度后，和原始 REINFORCE 一样用随机策略梯度上升更新策略网络 ${\pi }_{\theta }(a|s)$
  • 可以用基线来改进 actor-critic，得到的方法叫做 advantage actor-critic (A2C)。A2C 也有一个策略网络 ${\pi }_{\theta }(a|s)$ 和一个价值网络 $v_{\omega }(s)$。它使用 TD 算法（Sarsa）来更新价值网络计算随机策略梯度，并同样用梯度上升更新策略网络 ${\pi }_{\theta }(a|s)$。为了稳定 TD bootstarp，可以像 DQN 那样引入目标价值网络 $v_{{\omega }^{\prime }}(s)$ 用于计算 TD target，目标网络通过加权平均方式进行 soft update，可以进一步提高 A2C 的性能