机器学习笔记之优化算法(三)线搜索方法(步长角度;精确搜索)
机器学习笔记之优化算法——线搜索方法[步长角度,精确搜索]
- 引言
-
- 回顾:线搜索方法——方向角度
-
- 关于收敛性的假设
- 关于单调性的假设
- 下降方向与最速方向
- 从步长角度观察线搜索方法
-
- 关于方向向量的假设
- 精确搜索过程
引言
上一节介绍了从方向角度认识线搜索方法,本节继续介绍:从步长角度认识线搜索方法。
回顾:线搜索方法——方向角度
关于线搜索方法的迭代过程表示如下:
x k + 1 = x k + α k ⋅ P k x_{k+1} = x_k + \alpha_k \cdot \mathcal P_k xk+1=xk+αk⋅Pk
关于收敛性的假设
关于目标函数: f ( X ) f(\mathcal X) f(X),我们通过求解一系列数值解 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞的方式使得:
- 随着迭代次数 k k k的增加,对应的 f ( x k ) f(x_k) f(xk)能够有效地收敛,最终得到目标函数的最小值: min X ∈ R n f ( X ) \begin{aligned}\mathop{\min}\limits_{\mathcal X \in \mathbb R^{n}} f(\mathcal X)\end{aligned} X∈Rnminf(X),从而得到数值解的最优值 x ∗ x^* x∗:
x ∗ = arg min X ∈ R n f ( X ) x^* = \mathop{\arg\min}\limits_{\mathcal X \in \mathbb R^n} f(\mathcal X) x∗=X∈Rnargminf(X)
关于单调性的假设
为了简化逻辑,我们仅讨论各迭代步骤的数值解 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞对应的目标函数结果 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞服从严格的单调性。即:
其中 N N N表示非负整数。
∀ k ∈ N ⇒ f ( x k + 1 ) < f ( x k ) \forall k \in N \Rightarrow f(x_{k+1}) < f(x_k) ∀k∈N⇒f(xk+1)<f(xk)
下降方向与最速方向
基于上一节的相关假设,我们可以得到如下结论:
f ( x k + 1 ) − f ( x k ) ≈ [ ∇ f ( x k ) ] T ⋅ P k < 0 f(x_{k+1}) - f(x_k) \approx \left[\nabla f(x_k)\right]^T \cdot \mathcal P_k < 0 f(xk+1)−f(xk)≈[∇f(xk)]T⋅Pk<0
将上式继续展开:
∣ ∣ ∇ f ( x k ) ∣ ∣ ⋅ ∣ ∣ P k ∣ ∣ cos θ < 0 ||\nabla f(x_k)|| \cdot ||\mathcal P_k|| \cos \theta < 0 ∣∣∇f(xk)∣∣⋅∣∣Pk∣∣cosθ<0
从上式可以看出:
-
∣ ∣ ∇ f ( x k ) ∣ ∣ ||\nabla f(x_k)|| ∣∣∇f(xk)∣∣与 ∣ ∣ P k ∣ ∣ ||\mathcal P_k|| ∣∣Pk∣∣分别表示向量 ∇ f ( x k ) , P k \nabla f(x_k),\mathcal P_k ∇f(xk),Pk的模,因而它们恒正。因而向量 ∇ f ( x k ) , P k \nabla f(x_k),\mathcal P_k ∇f(xk),Pk之间的夹角 θ ∈ ( π 2 , 3 π 2 ) \theta \in \left(\begin{aligned}\frac{\pi}{2},\frac{3\pi}{2}\end{aligned} \right) θ∈(2π,23π)。见下图:
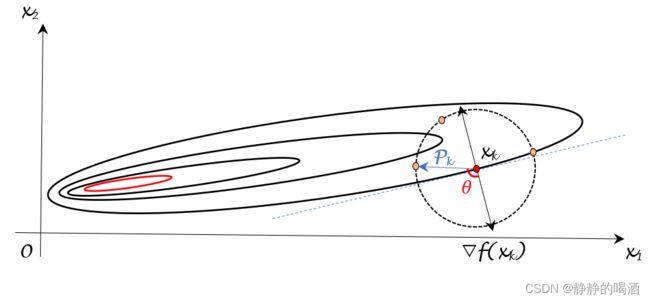
其中蓝色虚线上方的部分表示 θ ∈ ( π 2 , 3 π 2 ) \theta \in \left(\begin{aligned}\frac{\pi}{2},\frac{3\pi}{2}\end{aligned} \right) θ∈(2π,23π)的区间,由于 P k \mathcal P_k Pk是单位向量,因此蓝色虚线上方圆上的点构成的单位向量 P k \mathcal P_k Pk都可以使 f ( x k + 1 ) < f ( x k ) f(x_{k+1}) < f(x_k) f(xk+1)<f(xk),我们称这些方向为下降方向 ( Descent Direction ) (\text{Descent Direction}) (Descent Direction); -
由于 x k x_k xk是上一次迭代产生的数值解,因而 ∣ ∣ ∇ f ( x k ) ∣ ∣ ||\nabla f(x_k)|| ∣∣∇f(xk)∣∣是确定的;并且 ∣ ∣ P k ∣ ∣ = 1 ||\mathcal P_k|| = 1 ∣∣Pk∣∣=1,如何使 ∣ ∣ ∇ f ( x k ) ∣ ∣ ⋅ ∣ ∣ P k ∣ ∣ cos θ ||\nabla f(x_k)|| \cdot ||\mathcal P_k|| \cos \theta ∣∣∇f(xk)∣∣⋅∣∣Pk∣∣cosθ达到最小,只能通过调整方向( θ \theta θ)来获取最小值。
当 θ = π \theta = \pi θ=π时, cos θ \cos \theta cosθ取得最小值 − 1 -1 −1。这意味着:当向量 P k \mathcal P_k Pk与梯度向量 ∇ f ( x k ) \nabla f(x_k) ∇f(xk)方向相反时,可取得当前迭代步骤的最优方向。该方向也被称作最速下降方向 ( Steepest Descent Direction ) (\text{Steepest Descent Direction}) (Steepest Descent Direction)。而梯度下降法也被称作最速下降法。
从步长角度观察线搜索方法
关于方向向量的假设
在观察步长的过程中,我们同样需要固定住方向信息。我们首先假定向量 P k \mathcal P_k Pk的方向是下降方向而非最速下降方向;
也可以说:下降方向需要向量 P k \mathcal P_k Pk与负梯度向量 − ∇ f ( x k ) -\nabla f(x_k) −∇f(xk)之间的夹角是锐角:
之所以上一节将其范围描述为 ( − π 2 , π 2 ) \begin{aligned} \left(-\frac{\pi}{2},\frac{\pi}{2}\right)\end{aligned} (−2π,2π),是因为这种描述方法是将 − ∇ f ( x k ) -\nabla f(x_k) −∇f(xk)方向固定,仅对 P k \mathcal P_k Pk方向进行约束。但实际上:向量 P k \mathcal P_k Pk与向量 − ∇ f ( x k ) -\nabla f(x_k) −∇f(xk)之间夹角和向量 − ∇ f ( x k ) -\nabla f(x_k) −∇f(xk)与向量 P k \mathcal P_k Pk之间夹角之间没有区别。因而可将其夹角范围描述为 ( 0 , π 2 ) \begin{aligned} \left(0,\frac{\pi}{2} \right)\end{aligned} (0,2π)。
− [ ∇ f ( x k ) ] T P k > 0 ⇒ [ ∇ f ( x k ) ] T P k < 0 - \left[\nabla f(x_k)\right]^T \mathcal P_k > 0 \Rightarrow \left[\nabla f(x_k)\right]^T \mathcal P_k < 0 −[∇f(xk)]TPk>0⇒[∇f(xk)]TPk<0
精确搜索过程
关于步长 α k \alpha_k αk,我们在优化算法——无约束优化概述中介绍过:无论 α k \alpha_k αk较大还是较小,都会产生负面影响:
- 步长过大,可能会导致即便方向 P k \mathcal P_k Pk正确,但依然使得 f ( x k + 1 ) > f ( x k ) f(x_{k+1}) > f(x_k) f(xk+1)>f(xk),从而使本次迭代产生的 x k + 1 x_{k+1} xk+1无效;
- 步长过小,相比于步长过大确实能够更少地出现迭代无效的情况,但一直使用较小步长反而在迭代过程中出现不必要的计算代价。
思考:在方向向量 P k \mathcal P_k Pk是下降方向的条件下,如何去选择合适的步长 α k \alpha_k αk ? ? ?一个朴素的想法是:使 f ( x k + 1 ) f(x_{k+1}) f(xk+1)达到最小的步长就是最优步长:
这里的 P k \mathcal P_k Pk是给定的, x k x_k xk也是给定的,说明该优化问题是一个关于 α \alpha α的一次的优化问题,因此也将线搜索方法称作一维搜索方法。
α k = arg min α > 0 f ( x k + 1 ) = arg min α > 0 f ( x k + α ⋅ P k ) = { arg min α > 0 ϕ ( α ) ϕ ( α ) ≜ f ( x k + α ⋅ P k ) \begin{aligned} \alpha_k & = \mathop{\argmin}\limits_{\alpha > 0} f(x_{k+1}) \\ & = \mathop{\argmin}\limits_{\alpha > 0} f(x_k + \alpha \cdot \mathcal P_k) \\ & = \begin{cases} \mathop{\argmin}\limits_{\alpha > 0} \phi(\alpha) \\\phi(\alpha) \triangleq f(x_k + \alpha \cdot \mathcal P_k) \end{cases} \end{aligned} αk=α>0argminf(xk+1)=α>0argminf(xk+α⋅Pk)=⎩ ⎨ ⎧α>0argminϕ(α)ϕ(α)≜f(xk+α⋅Pk)
很明显,这就是仅关于 α \alpha α的一元函数,在 α > 0 \alpha > 0 α>0约束条件下求解它的最值是简单的。这种求解步长 α k \alpha_k αk的方式被称作精确搜索方法。
既然是要计算 ϕ ( α ) \phi(\alpha) ϕ(α)的最值,首先对该函数的梯度进行描述:
∂ ϕ ( α ) ∂ α = ϕ ′ ( α ) = [ ∇ f ( x k + α ⋅ P k ) ] T ⋅ P k \begin{aligned} \frac{\partial \phi(\alpha)}{\partial \alpha} & = \phi'(\alpha) \\ & = \left[\nabla f(x_k + \alpha \cdot \mathcal P_k)\right]^T \cdot \mathcal P_k \end{aligned} ∂α∂ϕ(α)=ϕ′(α)=[∇f(xk+α⋅Pk)]T⋅Pk
虽然我们并不清楚函数 ϕ ( α ) \phi(\alpha) ϕ(α)的具体形状,但不妨碍我们对该函数中一些特殊点对应的实际意义:
-
α = 0 ⇒ ϕ ( α ) = f ( x k ) \alpha = 0 \Rightarrow \phi(\alpha) = f(x_k) α=0⇒ϕ(α)=f(xk);
当然,根据α \alpha α的定义域,它是不可能取到0 0 0的。但确实存在实际意义:当步长为0 0 0时,x k + 1 = x k x_{k+1} = x_k xk+1=xk;关于 α = 0 \alpha = 0 α=0时的梯度 ϕ ′ ( 0 ) \phi'(0) ϕ′(0)可以表示为:
这正是关于方向向量P k \mathcal P_k Pk的假设。也就是说,函数ϕ ( α ) \phi(\alpha) ϕ(α)在零点处的斜率是负值。
ϕ ′ ( 0 ) = [ ∇ f ( x k ) ] T P k < 0 \phi'(0) = \left[\nabla f(x_k)\right]^T \mathcal P_k < 0 ϕ′(0)=[∇f(xk)]TPk<0
我们可以尝试认知一下零点处的切线方程:
这个关于α \alpha α的一元一次方程斜率是[ ∇ f ( x k ) ] T P k \left[\nabla f(x_k)\right]^T \mathcal P_k [∇f(xk)]TPk,并且过点[ 0 , f ( x k ) ] [0,f(x_k)] [0,f(xk)]点。
L ( α ) = [ ∇ f ( x k ) ] T P k ⋅ α + f ( x k ) \mathcal L(\alpha) = [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha + f(x_k) L(α)=[∇f(xk)]TPk⋅α+f(xk)
从管中窥豹的观察,我们可以做一个简单认知: ϕ ( α ) \phi(\alpha) ϕ(α)自身是一个过 [ 0 , f ( x k ) ] [0,f(x_k)] [0,f(xk)],初始梯度是负值的一个复杂函数。如果想要求解它的最值,仅需要令 ∂ ϕ ( α ) ∂ α ≜ 0 \begin{aligned}\frac{\partial \phi(\alpha)}{\partial \alpha} \triangleq 0 \end{aligned} ∂α∂ϕ(α)≜0从而求解出 α \alpha α的最值结果。
虽然 ϕ ( α ) \phi(\alpha) ϕ(α)仅包含一个,并且仅有一次的未知项 α \alpha α,但实际情况下,它的求解并不简单。其核心原因是:我们不清楚目标函数 f ( ⋅ ) f(\cdot) f(⋅)的复杂程度。
这取决于模型、以及任务类型。
首先,目标函数f ( x k + α ⋅ P k ) f(x_k + \alpha \cdot \mathcal P_k) f(xk+α⋅Pk)自身就是一个复杂函数,并且它的梯度∇ f ( x k + α ⋅ P k ) \nabla f(x_k + \alpha \cdot \mathcal P_k) ∇f(xk+α⋅Pk)同样也是复杂的。关于梯度∇ f ( x k + α ⋅ P k ) \nabla f(x_k + \alpha \cdot \mathcal P_k) ∇f(xk+α⋅Pk)并不是仅计算一次,而是每一次迭代过程中都要计算梯度。这使得计算代价可能极高。
该步骤实际上也是一个求解解析解的过程,但实际上我们对每次迭代精确求解最优步长是没有必要的。我们只希望迭代产生的 f ( x k ) f(x_k) f(xk)收敛即可。
下一节我们将讨论:是否可以使用非精确搜索来近似每次迭代步长的最优解。
相关参考:
【优化算法】线搜索方法-步长-精确搜索