RL 实践(7)—— CartPole【TPRO & PPO】
- 本文介绍 PPO 这个 online RL 的经典算法,并在 CartPole-V0 上进行测试。由于 PPO 是源自 TPRO 的,因此也会在原理部分介绍 TPRO
- 参考:张伟楠《动手学强化学习》、王树森《深度强化学习》
- 完整代码下载:8_[Gym] CartPole-V0 (PPO)
文章目录
- 1. TPRO(置信域策略优化)方法
-
- 1.1 朴素策略梯度方法的问题
- 1.2 置信域优化法
- 1.3 TPRO 公式推导
-
- 1.3.1 做近似
- 1.3.2 最大化
- 1.4 小结
- 2. PPO(近端策略优化)方法
-
- 2.1 PPO 公式推导
-
- 2.1.1 做近似
- 2.1.2 最大化
- 2.2 伪代码
- 2.3 用 PPO 方法解决 CartPole 问题
- 3. 总结
1. TPRO(置信域策略优化)方法
- 置信域策略优化 (Trust Region Policy Optimization, TRPO) 是一种策略学习方法,跟朴素的策略梯度方法相比有两个优势:
- TRPO表现更稳定,收敛曲线不会剧烈波动,而且对学习率不敏感
- TRPO 用更少的经验数据(transition 四元组)就能达到与策略梯度方法相同的表现
1.1 朴素策略梯度方法的问题
- 前文已经介绍了 policy gradient 方法 REINFORCE & Actor-Critic 以及其带 baseline 的改进版本 REINFORCE with baseline & A2C。这些方法的核心思想都是:参数化 agent 策略 π θ \pi_\theta πθ,设计衡量策略好坏的目标函数 J ( θ ) = E s [ V π θ ( s ) ] = E π θ [ ∑ t = 0 ∞ γ t r ( s t , a t ) ] J(\theta)=\mathbb{E}_{s}[V_{\pi_\theta}(s)] = \mathbb{E}_{\pi_\theta}[\sum_{t=0}^\infin \gamma^tr(s_t,a_t)] J(θ)=Es[Vπθ(s)]=Eπθ[t=0∑∞γtr(st,at)]通过梯度上升的方法找出最大化这个目标函数的策略参数 θ ∗ = arg max θ J ( θ ) \theta^* =\argmax_\theta J(\theta) θ∗=argmaxθJ(θ),从而得到最优策略 π θ ∗ \pi_{\theta^*} πθ∗
- 但是这种算法有一个明显的缺点:注意到在环境中 rollout 时,策略 π θ \pi_\theta πθ 会被重复使用,即使策略只有微小的改变,也可能导致最终收益的巨大变化。当策略网络是深度模型时这种特性尤其明显,因此在沿着策略梯度方向更新参数时
θ ← θ + β ▽ θ J ( θ ) \theta \leftarrow \theta + \beta \triangledown_\theta J(\theta) θ←θ+β▽θJ(θ) 很有可能由于步长 β \beta β 太长导致策略突然显著变差,进而影响训练效果。宏观上看就是朴素的策略梯度方法训练不够稳定 - 针对以上问题,TPRO 的思想是在更新时找到一块信任区域(trust region),认为在这个区域上更新策略时能够得到某种策略性能的安全性保证,从而避免策略崩溃
为了实现这种安全性保证,我们必须舍弃掉随机梯度上升而改用其他的优化算法,TPRO 选择了置信域方法 (Trust Region Methods)
1.2 置信域优化法
-
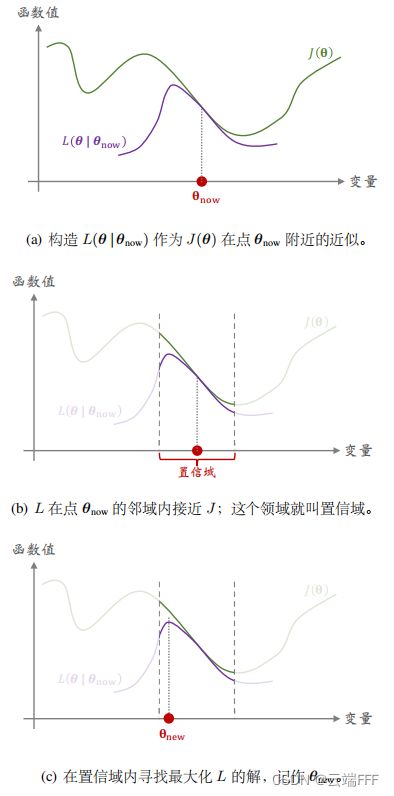
置信域优化法是数值最优化领域中一类经典的算法,历史至少可以追溯到 1970 年。其出发点是:如果对目标函数 J ( θ ) J(\theta) J(θ) 进行优化过于困难,不妨构造一个替代函数 L ( θ ∣ θ n o w ) L(\theta|\theta_{now}) L(θ∣θnow),要求替代函在 θ \theta θ 的当前值 θ n o w \theta_{now} θnow 的邻域 N ( θ n o w ) \mathcal{N}(\theta_{now}) N(θnow) 内和 J ( θ ) J(\theta) J(θ) 十分相似的,通过在这个局部范围内最优化 L ( θ ∣ θ n o w ) L(\theta|\theta_{now}) L(θ∣θnow) 来更新一次 θ \theta θ 值,反复迭代上述过程直到收敛
其中 N ( θ n o w ) \mathcal{N}(\theta_{now}) N(θnow) 就被称作
置信域,顾名思义,在 θ n o w \theta_{now} θnow 的邻域上我们可以信任 L ( θ ∣ θ n o w ) L(\theta|\theta_{now}) L(θ∣θnow),可以拿它来替代目标函数 J ( θ ) J(\theta) J(θ)具体而言每轮迭代可以分成两步
- 做近似:给定 θ n o w \theta_{now} θnow,构造函数 L ( θ ∣ θ n o w ) L(\theta| \theta_{now}) L(θ∣θnow),使得对于所有的 θ ∈ N ( θ n o w ) θ \in\mathcal{N}(\theta_{now}) θ∈N(θnow)(置信域内取值),函数值 L ( θ ∣ θ n o w ) L(\theta| \theta_{now}) L(θ∣θnow) 与原优化目标 J ( θ ) J(\theta) J(θ) 足够接近
- 最大化: 在置信域 N ( θ n o w ) \mathcal{N}(\theta_{now}) N(θnow) 中寻找变量 θ \theta θ 的值,使得替代函数 L L L 的值最大化。即求 θ n e w = arg max θ ∈ N ( θ n o w ) L ( θ ∣ θ n o w ) \theta_{new} = \argmax_{\theta \in \mathcal{N}(\theta_{now})}L(\theta|\theta_{now}) θnew=θ∈N(θnow)argmaxL(θ∣θnow)
-
注意到置信域半径控制着每一轮迭代中 θ \theta θ 变化的上限,我们通常会让这个半径随优化过程不断减小来避免 overstep
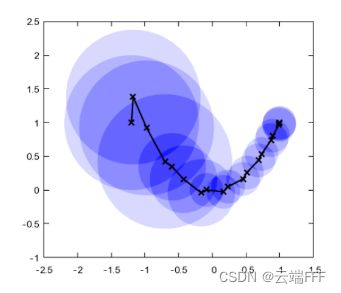
-
置信域方法是一种算法框架而非一个具体的算法。有很多种方式实现实现置信域方法:
- 第一步做近似的方法有多种多样,比如蒙特卡洛、二阶泰勒展开等
- 第二步解一个约束最大化问题的方法也很多,包括梯度投影算法、拉格朗日法等
- 置信域 N ( θ n o w ) \mathcal{N}(\theta_{now}) N(θnow) 也有多种多样的选择,既可以是球,也可以是两个概率分布的 KL 散度等
1.3 TPRO 公式推导
- TPRO 是一种将置信域优化方法应用到策略学习中的 Online RL 方法。回顾 policy gradient 算法,优化目标为最大化
J ( θ ) = E S ∼ d π θ [ V π θ ( S ) ] = E S ∼ d π θ [ E A ∼ π θ ( ⋅ ∣ S ) [ Q π θ ( S , A ) ] ] (1) \begin{aligned} J(\theta) &=\mathbb{E}_{S\sim d^{\pi_{\theta}}}[V_{\pi_\theta}(S)] \\ &=\mathbb{E}_{S\sim d^{\pi_{\theta}}}\big[\mathbb{E}_{A\sim\pi_\theta(·|S)}[Q_{\pi_\theta}(S,A)]\big] \end{aligned} \tag{1} J(θ)=ES∼dπθ[Vπθ(S)]=ES∼dπθ[EA∼πθ(⋅∣S)[Qπθ(S,A)]](1) 其中 d π θ d^{\pi_{\theta}} dπθ 是策略 π θ \pi_\theta πθ 诱导的状态分布。考虑置信域优化法的迭代过程,每一步我们要构造优化问题:基于当前的参数 θ n o w \theta_{now} θnow 优化 θ \theta θ,故在式1中引入 θ n o w \theta_{now} θnow
J ( θ ∣ θ n o w ) = E S ∼ d π θ [ E A ∼ π θ ( ⋅ ∣ S ) [ Q π θ ( S , A ) ] ] = E S ∼ d π θ [ E A ∼ π θ n o w ( ⋅ ∣ S ) [ π θ ( A ∣ S ) π θ n o w ( A ∣ S ) ⋅ Q π θ ( S , A ) ] ] (2) \begin{aligned} J(\theta|\theta_{now}) &=\mathbb{E}_{S\sim d^{\pi_{\theta}}}\big[\mathbb{E}_{A\sim\pi_\theta(·|S)}[Q_{\pi_\theta}(S,A)]\big] \\ &=\mathbb{E}_{S\sim d^{\pi_{\theta}}}\left[\mathbb{E}_{A\sim\pi_{\theta_{now}}(·|S)}\left[\frac{ \pi_{\theta}(A|S) }{\pi_{\theta_{now}}(A|S)}\cdot Q_{\pi_\theta}(S,A)\right]\right] \\ \end{aligned} \tag{2} J(θ∣θnow)=ES∼dπθ[EA∼πθ(⋅∣S)[Qπθ(S,A)]]=ES∼dπθ[EA∼πθnow(⋅∣S)[πθnow(A∣S)πθ(A∣S)⋅Qπθ(S,A)]](2) 注意 J ( θ ∣ θ n o w ) J(\theta|\theta_{now}) J(θ∣θnow) 是关于 θ \theta θ 的函数,含有 θ n o w \theta_{now} θnow 的成分都可以看做常数,故以上是一个恒等变换。下面开始推导每轮迭代的两个关键步骤
1.3.1 做近似
- 原始优化目标 J ( θ ∣ θ n o w ) J(\theta|\theta_{now}) J(θ∣θnow) 中 d π θ d^{\pi_{\theta}} dπθ 和 Q θ Q_\theta Qθ 都不知道,无法直接优化,需要进行三步近似来构造替代函数
- 用当前策略 π θ n o w \pi_{\theta_{now}} πθnow 诱导的状态分布 d π θ n o w d^{\pi_{\theta_{now}}} dπθnow 近似 d π θ d^{\pi_{\theta}} dπθ,原始优化目标近似为
E S ∼ d π θ n o w [ E A ∼ π θ n o w ( ⋅ ∣ S ) [ π θ ( A ∣ S ) π θ n o w ( A ∣ S ) ⋅ Q π θ ( S , A ) ] ] \mathbb{E}_{S\sim d^{\pi_{\theta_{now}}}}\left[\mathbb{E}_{A\sim\pi_{\theta_{now}}(·|S)}\left[\frac{ \pi_{\theta}(A|S) }{\pi_{\theta_{now}}(A|S)}\cdot Q_{\pi_\theta}(S,A)\right]\right] ES∼dπθnow[EA∼πθnow(⋅∣S)[πθnow(A∣S)πθ(A∣S)⋅Qπθ(S,A)]] - 用 MC 近似消去上式中的两个期望。具体而言,先用当前策略 π θ n o w \pi_{\theta_{now}} πθnow 和环境交互收集一条轨迹
s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . , s n , a n , r n s_1, a_1, r_1, s_2, a_2, r_2,...,s_n, a_n, r_n s1,a1,r1,s2,a2,r2,...,sn,an,rn 此轨迹满足 s t ∼ d π θ n o w , a t ∼ π θ n o w ( ⋅ ∣ s t ) s_t\sim d^{\pi_{\theta_{now}}}, a_t\sim \pi_{\theta_{now}}(·|s_t) st∼dπθnow,at∼πθnow(⋅∣st),故每个 ( s t , a t ) (s_t,a_t) (st,at) 二元组都能构造一个无偏 MC 估计
π θ ( a t ∣ s t ) π θ n o w ( a t ∣ s t ) ⋅ Q π θ ( a t , s t ) \frac{ \pi_{\theta}(a_t|s_t) }{\pi_{\theta_{now}}(a_t|s_t)}\cdot Q_{\pi_\theta}(a_t,s_t) πθnow(at∣st)πθ(at∣st)⋅Qπθ(at,st) 用这些无偏估计的期望(均值)来近似原始优化目标,得到
1 n ∑ t = 1 n π θ ( a t ∣ s t ) π θ n o w ( a t ∣ s t ) ⋅ Q π θ ( a t , s t ) \frac{1}{n}\sum_{t=1}^n \frac{ \pi_{\theta}(a_t|s_t) }{\pi_{\theta_{now}}(a_t|s_t)}\cdot Q_{\pi_\theta}(a_t,s_t) n1t=1∑nπθnow(at∣st)πθ(at∣st)⋅Qπθ(at,st) - 用真实 return 对 Q π θ ( a t , s t ) Q_{\pi_\theta}(a_t,s_t) Qπθ(at,st) 进行 MC 近似,具体而言
Q π θ ( a t , s t ) ⟹ Q π θ n o w ( a t , s t ) ⟹ u t = r t + γ r t + 1 + γ 2 r t + 2 + . . . + γ n − t r n Q_{\pi_\theta}(a_t,s_t) \quad\Longrightarrow\quad Q_{\pi_{\theta_{now}}}(a_t,s_t) \quad\Longrightarrow\quad u_t=r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + ...+ \gamma^{n-t} r_{n} Qπθ(at,st)⟹Qπθnow(at,st)⟹ut=rt+γrt+1+γ2rt+2+...+γn−trn
- 用当前策略 π θ n o w \pi_{\theta_{now}} πθnow 诱导的状态分布 d π θ n o w d^{\pi_{\theta_{now}}} dπθnow 近似 d π θ d^{\pi_{\theta}} dπθ,原始优化目标近似为
- 综上得到对优化目标 J ( θ ∣ θ n o w ) J(\theta|\theta_{now}) J(θ∣θnow) 的近似
L ( θ ∣ θ n o w ) = 1 n ∑ t = 1 n π θ ( a t ∣ s t ) π θ n o w ( a t ∣ s t ) ⋅ u t (3) L(\theta|\theta_{now}) = \frac{1}{n}\sum_{t=1}^n \frac{ \pi_{\theta}(a_t|s_t) }{\pi_{\theta_{now}}(a_t|s_t)}\cdot u_t \tag{3} L(θ∣θnow)=n1t=1∑nπθnow(at∣st)πθ(at∣st)⋅ut(3) 注意近似过程中假设了 π θ \pi_{\theta} πθ 和 π θ n o w \pi_{\theta_{now}} πθnow 极其接近,以至于可以认为二者诱导的状态分布一致,这样就能完全避免策略优化后进入坏状态引发 1.1 节的 overstep 问题。因此需要强调置信域:只有 θ \theta θ 靠近 θ n o w \theta_{now} θnow 时才是有效近似。
1.3.2 最大化
-
每轮迭代中,求解以下约束优化问题
max θ L ( θ ∣ θ n o w ) s.t θ ∈ N ( θ n o w ) . \max_\theta L(\theta|\theta_{now}) \quad \text{s.t} \quad\theta\in\mathcal{N}(\theta_{now}). θmaxL(θ∣θnow)s.tθ∈N(θnow). 我们认为在置信域 N ( θ n o w ) \mathcal{N}(\theta_{now}) N(θnow) 内 d π θ n o w d^{\pi_{\theta_{now}}} dπθnow 近似 d π θ d^{\pi_{\theta}} dπθ,这个约束越紧,就越能避免 1.1 节的 overstep 问题 -
邻域(置信域) N ( θ n o w ) \mathcal{N}(\theta_{now}) N(θnow) 的选取方法通常有两种
- 简单地设置一个关于参数的欧式距离的阈值 △ \triangle △,即 ∣ ∣ θ − θ n o w ∣ ∣ 2 ≤ △ ||\theta-\theta_{now}||_2 \leq \triangle ∣∣θ−θnow∣∣2≤△ 这时置信域是以 θ n o w \theta_{now} θnow 为球心, △ \triangle △ 为半径的超球。这种选择可以让约束优化问题的求解容易一些
- 另一种方式是设置一个关于策略的 KL 散度的阈值 △ \triangle △,即
E S ∼ d π θ n o w D KL [ π θ n o w ( ⋅ ∣ S ) ∣ ∣ π θ ( ⋅ ∣ S ) ] ≤ △ \mathbb{E}_{S\sim d^{\pi_{\theta_{now}}}} D_\text{KL}\big[\pi_{\theta_{now}}(·|S) || \pi_{\theta}(·|S) \big] \leq \triangle ES∼dπθnowDKL[πθnow(⋅∣S)∣∣πθ(⋅∣S)]≤△ 此 KL 散度同样用 1.3.1 节中 π θ n o w \pi_{\theta_{now}} πθnow 交互得到的轨迹来做 MC 近似计算,即
1 n ∑ t = 1 n D KL [ π θ n o w ( ⋅ ∣ s t ) ∣ ∣ π θ ( ⋅ ∣ s t ) ] ≤ △ \frac{1}{n} \sum_{t=1}^n D_\text{KL}\big[\pi_{\theta_{now}}(·|s_t) || \pi_{\theta}(·|s_t) \big] \leq \triangle n1t=1∑nDKL[πθnow(⋅∣st)∣∣πθ(⋅∣st)]≤△ 这种做法可以直接约束策略的变化程度。实践表明这种置信域设定表现较好,对于 RL 来说,约束 “行为上的距离” 可能比约束 “参数上的距离” 更加合适
-
综上得到每轮迭代的约束优化问题为
max θ 1 n ∑ t = 1 n π θ ( a t ∣ s t ) π θ n o w ( a t ∣ s t ) ⋅ u t s.t. 1 n ∑ t = 1 n D KL [ π θ n o w ( ⋅ ∣ s t ) ∣ ∣ π θ ( ⋅ ∣ s t ) ] ≤ △ where s t ∼ d π θ n o w , a t ∼ π θ n o w ( ⋅ ∣ s t ) \begin{aligned} &\max_\theta&&\frac{1}{n}\sum_{t=1}^n \frac{ \pi_{\theta}(a_t|s_t) }{\pi_{\theta_{now}}(a_t|s_t)}\cdot u_t \\ &\text{s.t.} &&\frac{1}{n} \sum_{t=1}^n D_\text{KL}\big[\pi_{\theta_{now}}(·|s_t) || \pi_{\theta}(·|s_t) \big] \leq \triangle \\ & \text{where} && s_t\sim d^{\pi_{\theta_{now}}}, a_t\sim \pi_{\theta_{now}}(·|s_t) \end{aligned} θmaxs.t.wheren1t=1∑nπθnow(at∣st)πθ(at∣st)⋅utn1t=1∑nDKL[πθnow(⋅∣st)∣∣πθ(⋅∣st)]≤△st∼dπθnow,at∼πθnow(⋅∣st) 这个问题求解起来很麻烦,大概思路是- 对优化目标在 θ n o w \theta_{now} θnow 处进行一阶泰勒展开
- 对约束函数在 θ n o w \theta_{now} θnow 处进行二阶泰勒展开
- 用拉格朗日乘子法转换为无约束优化问题,通过 KKT 条件得到 θ \theta θ 的最优解
其中二阶泰勒展开带来的黑塞矩阵尺寸很大,编程时要使用共轭梯度法进行处理;另外由于泰勒展开近似得不到精确解,还要用线性搜索来确保约束条件满足,这些问题导致 TPRO 实现复杂,没有大规模流行
1.4 小结
- 置信域方法指的是一大类数值优化算法,通常用于求解非凸问题。对于一个最大化问题,算法重复两个步骤——做近似、最大化——直到算法收敛
- 置信域策略优化(TRPO)是一种利用置信域算法优化策略的 On-policy Online RL 方法,它的优化目标和策略梯度方法相同,每次策略训练仅使用上一轮策略采样的数据,是 policy-based 类算法中十分有代表性的工作之一。直觉性地理解,TRPO 给出的观点是:由于策略的改变导致数据分布的改变,这大大影响深度模型实现的策略网络的学习效果,所以通过划定一个可信任的策略学习区域,保证策略学习的稳定性和有效性
- TRPO中有两个需要调的超参数:一个是置信域的半径 △ \triangle △,另一个是求解最大化问题的数值算法的学习率。通常来说, △ \triangle △ 在算法的运行过程中要逐渐缩小。虽然TRPO需要调参,但是TRPO对超参数的设置并不敏感,即使超参数设置不够好,TRPO的表现也不会太差。相比之下,策略梯度算法对超参数更敏感
- TPRO 的优势在于更好的稳定性和更高的样本效率;缺点在于每步迭代求解约束优化问题的过程繁琐,算法实现复杂 ,其后续工作 PPO 很好地解决了此问题,成为了非常流行的 Online RL 方法
2. PPO(近端策略优化)方法
- PPO 基于 TRPO 的思想,但是其算法实现更加简单。大量的实验结果表明,PPO 能和 TRPO 学习得一样好且收敛更快,这使得 PPO 和 SAC、TD3 一起成为三大最流行的强化学习算法。如果我们想要尝试在一个新的环境中使用强化学习,可以首先尝试这三个算法
- PPO 算法框架和 TPRO 无异,其核心思想在于将 “最大化” 操作中的约束优化问题转换为无约束优化来简化问题
2.1 PPO 公式推导
- 前文 1.3 节推 TPRO 优化目标时是从 policy gradient 法的原始优化目标开始推导的,那样推比较简单,得到优化目标为
J ( θ ∣ θ n o w ) = E S ∼ d π θ [ E A ∼ π θ n o w ( ⋅ ∣ S ) [ π θ ( A ∣ S ) π θ n o w ( A ∣ S ) ⋅ Q π θ ( S , A ) ] ] J(\theta|\theta_{now}) = \mathbb{E}_{S\sim d^{\pi_{\theta}}}\left[\mathbb{E}_{A\sim\pi_{\theta_{now}}(·|S)}\left[\frac{ \pi_{\theta}(A|S) }{\pi_{\theta_{now}}(A|S)}\cdot Q_{\pi_\theta}(S,A)\right]\right] J(θ∣θnow)=ES∼dπθ[EA∼πθnow(⋅∣S)[πθnow(A∣S)πθ(A∣S)⋅Qπθ(S,A)]] 但 TPRO 和 PPO 的原始论文中使用了另一种推导方法,最后得到的优化目标略有不同,为
J ( θ ∣ θ n o w ) = E S ∼ d π θ [ E A ∼ π θ n o w ( ⋅ ∣ S ) [ π θ ( A ∣ S ) π θ n o w ( A ∣ S ) ⋅ A π θ n o w ( S , A ) ] ] J(\theta|\theta_{now}) = \mathbb{E}_{S\sim d^{\pi_{\theta}}}\left[\mathbb{E}_{A\sim\pi_{\theta_{now}}(·|S)}\left[\frac{ \pi_{\theta}(A|S) }{\pi_{\theta_{now}}(A|S)}\cdot A_{\pi_{\theta_{now}}}(S,A)\right]\right] J(θ∣θnow)=ES∼dπθ[EA∼πθnow(⋅∣S)[πθnow(A∣S)πθ(A∣S)⋅Aπθnow(S,A)]] 其中 A ( S , A ) A(S,A) A(S,A) 函数是前文 RL 实践(6)—— CartPole【REINFORCE with baseline & A2C】 中介绍的优势函数 A π ( s , a ) = △ Q π ( s , a ) − V π ( s ) A_\pi(s,a) \stackrel{\triangle}{=} Q_\pi(s,a) - V_\pi(s) Aπ(s,a)=△Qπ(s,a)−Vπ(s) 这两种优化目标都是可行的,由于 TPRO 和 PPO 的论文都用了后者,这里也推导一下这个目标 - 推导的出发点是希望借助当前参数 θ n o w \theta_{now} θnow 推导出新的 θ \theta θ 可以使得 J ( θ ) ≥ J ( θ n o w ) J(\theta)\geq J(\theta_{now}) J(θ)≥J(θnow)。这里优化目标设定为在初始状态分布 S 0 S_0 S0 下的状态价值期望 J ( θ ) = E S 0 [ V π θ ( S 0 ) ] J(\theta) = \mathbb{E}_{S_0}[V_{\pi_\theta}(S_0)] J(θ)=ES0[Vπθ(S0)],有
J ( θ ) = E S 0 [ V π θ ( S 0 ) ] = E s t ∼ d π θ [ ∑ t = 0 ∞ γ t V π θ ( s t ) − ∑ t = 1 ∞ γ t V π θ ( s t ) ] = − E s t ∼ d π θ [ ∑ t = 0 ∞ γ t ( γ V π θ ( s t + 1 ) − V π θ ( s t ) ) ] \begin{aligned} J(\theta) & =\mathbb{E}_{S_{0}}\left[V_{\pi_{\theta}}\left(S_{0}\right)\right] \\ & =\mathbb{E}_{s_t\sim d^{\pi_{\theta}}}\left[\sum_{t=0}^{\infty} \gamma^{t} V_{\pi_{\theta}}\left(s_{t}\right)-\sum_{t=1}^{\infty} \gamma^{t} V_{\pi_{\theta}}\left(s_{t}\right)\right] \\ & =-\mathbb{E}_{s_t\sim d^{\pi_{\theta}}}\left[\sum_{t=0}^{\infty} \gamma^{t}\left(\gamma V_{\pi_{\theta}}\left(s_{t+1}\right)-V_{\pi_{\theta}}\left(s_{t}\right)\right)\right] \end{aligned} J(θ)=ES0[Vπθ(S0)]=Est∼dπθ[t=0∑∞γtVπθ(st)−t=1∑∞γtVπθ(st)]=−Est∼dπθ[t=0∑∞γt(γVπθ(st+1)−Vπθ(st))] 考虑到策略诱导的状态分布和初始分布 S 0 S_0 S0 无关,当期望括号内仅和初始状态有关时,这个期望所关于的分布可以任意取,这样我们可以推导新旧策略的目标函数之间的差距
J ( θ ) − J ( θ n o w ) = E S 0 [ V π θ ( S 0 ) ] − E S 0 [ V π θ n o w ( S 0 ) ] = E s t ∼ d π θ [ ∑ t = 0 ∞ γ t r ( s t , a t ) ] + E s t ∼ d π θ [ ∑ t = 0 ∞ γ t ( γ V π θ n o w ( s t + 1 ) − V π θ n o w ( s t ) ) ] = E s t , a t ∼ d π θ [ ∑ t = 0 ∞ γ t [ r ( s t , a t ) + γ V π θ n o w ( s t + 1 ) − V π θ n o w ( s t ) ] ] = E s t , a t ∼ d π θ [ ∑ t = 0 ∞ γ t A π θ n o w ( s t , a t ) ] = 1 1 − γ E S ∼ d π θ [ E A ∼ π θ ( ⋅ ∣ s t ) [ A π θ n o w ( S , A ) ] ] \begin{aligned} J\left(\theta\right)-J(\theta_{now}) & =\mathbb{E}_{S_{0}}\left[V_{\pi_{\theta}}\left(S_{0}\right)\right]-\mathbb{E}_{S_{0}}\left[V_{\pi_{\theta_{now}}}\left(S_{0}\right)\right] \\ & =\mathbb{E}_{s_t\sim d^{\pi_{\theta}}}\left[\sum_{t=0}^{\infty} \gamma^{t} r\left(s_{t}, a_{t}\right)\right]+\mathbb{E}_{s_t\sim d^{\pi_{\theta}}}\left[\sum_{t=0}^{\infty} \gamma^{t}\left(\gamma V_{\pi_{\theta_{now}}}\left(s_{t+1}\right)-V_{\pi_{\theta_{now}}}\left(s_{t}\right)\right)\right] \\ & =\mathbb{E}_{s_t,a_t\sim d^{\pi_{\theta}}}\left[\sum_{t=0}^{\infty} \gamma^{t}\left[r\left(s_{t}, a_{t}\right)+\gamma V_{\pi_{\theta_{now}}}\left(s_{t+1}\right)-V_{\pi_{\theta_{now}}}\left(s_{t}\right)\right]\right]\\ & =\mathbb{E}_{s_t,a_t\sim d^{\pi_{\theta}}}\left[\sum_{t=0}^{\infty}\gamma^t A_{\pi_{\theta_{now}}}(s_t,a_t) \right]\\ &=\frac{1}{1-\gamma}\mathbb{E}_{S\sim d^{\pi_{\theta}}}\left[\mathbb{E}_{A\sim\pi_{\theta}(·|s_t)}\left[A_{\pi_{\theta_{now}}}(S,A)\right]\right] \end{aligned} J(θ)−J(θnow)=ES0[Vπθ(S0)]−ES0[Vπθnow(S0)]=Est∼dπθ[t=0∑∞γtr(st,at)]+Est∼dπθ[t=0∑∞γt(γVπθnow(st+1)−Vπθnow(st))]=Est,at∼dπθ[t=0∑∞γt[r(st,at)+γVπθnow(st+1)−Vπθnow(st)]]=Est,at∼dπθ[t=0∑∞γtAπθnow(st,at)]=1−γ1ES∼dπθ[EA∼πθ(⋅∣st)[Aπθnow(S,A)]] 故只要能找到一个新策略 π θ \pi_\theta πθ 使得 1 1 − γ E s t ∼ d π θ [ E a t ∼ π θ ( ⋅ ∣ s t ) [ A π θ n o w ( s t , a t ) ] ] ≥ 0 \frac{1}{1-\gamma}\mathbb{E}_{s_t\sim d^{\pi_{\theta}}}\left[\mathbb{E}_{a_t\sim\pi_{\theta}(·|s_t)}\left[A_{\pi_{\theta_{now}}}(s_t,a_t)\right]\right]\geq 0 1−γ1Est∼dπθ[Eat∼πθ(⋅∣st)[Aπθnow(st,at)]]≥0,就能保证策略性能单调递增 J ( θ ) ≥ J ( θ n o w ) J(\theta) \geq J(\theta_{now}) J(θ)≥J(θnow)。去掉其中常数部分再用重要度采样改为用 π θ n o w \pi_{\theta_{now}} πθnow 采样动作,就得到了 TPRO/PPO 的优化目标函数
J ( θ ∣ θ n o w ) = E S ∼ d π θ [ E A ∼ π θ n o w ( ⋅ ∣ S ) [ π θ ( A ∣ S ) π θ n o w ( A ∣ S ) ⋅ A π θ n o w ( S , A ) ] ] J(\theta|\theta_{now}) = \mathbb{E}_{S\sim d^{\pi_{\theta}}}\left[\mathbb{E}_{A\sim\pi_{\theta_{now}}(·|S)}\left[\frac{ \pi_{\theta}(A|S) }{\pi_{\theta_{now}}(A|S)}\cdot A_{\pi_{\theta_{now}}}(S,A)\right]\right] J(θ∣θnow)=ES∼dπθ[EA∼πθnow(⋅∣S)[πθnow(A∣S)πθ(A∣S)⋅Aπθnow(S,A)]]
2.1.1 做近似
- 得到替代函数的方法完全类似 1.3.1 节,进行三次近似即可。具体而言
-
用当前策略 π θ n o w \pi_{\theta_{now}} πθnow 诱导的状态分布 d π θ n o w d^{\pi_{\theta_{now}}} dπθnow 近似 d π θ d^{\pi_{\theta}} dπθ,原始优化目标近似为
E S ∼ d π θ n o w [ E A ∼ π θ n o w ( ⋅ ∣ S ) [ π θ ( A ∣ S ) π θ n o w ( A ∣ S ) ⋅ A π θ n o w ( S , A ) ] ] \mathbb{E}_{S\sim d^{\pi_{{\theta_{now}}}}}\left[\mathbb{E}_{A\sim\pi_{\theta_{now}}(·|S)}\left[\frac{ \pi_{\theta}(A|S) }{\pi_{\theta_{now}}(A|S)}\cdot A_{\pi_{\theta_{now}}}(S,A)\right]\right] ES∼dπθnow[EA∼πθnow(⋅∣S)[πθnow(A∣S)πθ(A∣S)⋅Aπθnow(S,A)]] -
用 MC 近似消去上式中的两个期望。具体而言,先用当前策略 π θ n o w \pi_{\theta_{now}} πθnow 和环境交互收集一条轨迹
s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . , s n , a n , r n s_1, a_1, r_1, s_2, a_2, r_2,...,s_n, a_n, r_n s1,a1,r1,s2,a2,r2,...,sn,an,rn 此轨迹满足 s t ∼ d π θ n o w , a t ∼ π θ n o w ( ⋅ ∣ s t ) s_t\sim d^{\pi_{\theta_{now}}}, a_t\sim \pi_{\theta_{now}}(·|s_t) st∼dπθnow,at∼πθnow(⋅∣st),故每个 ( s t , a t ) (s_t,a_t) (st,at) 二元组都能构造一个无偏 MC 估计
π θ ( a t ∣ s t ) π θ n o w ( a t ∣ s t ) ⋅ A π θ n o w ( a t , s t ) \frac{ \pi_{\theta}(a_t|s_t) }{\pi_{\theta_{now}}(a_t|s_t)}\cdot A_{\pi_{\theta_{now}}}(a_t,s_t) πθnow(at∣st)πθ(at∣st)⋅Aπθnow(at,st) 用这些无偏估计的期望(均值)来近似原始优化目标,得到
1 n ∑ t = 1 n π θ ( a t ∣ s t ) π θ n o w ( a t ∣ s t ) ⋅ A π θ n o w ( a t , s t ) \frac{1}{n}\sum_{t=1}^n \frac{ \pi_{\theta}(a_t|s_t) }{\pi_{\theta_{now}}(a_t|s_t)}\cdot A_{\pi_{\theta_{now}}}(a_t,s_t) n1t=1∑nπθnow(at∣st)πθ(at∣st)⋅Aπθnow(at,st) -
最后我们考虑如何估计优势函数 A π θ n o w ( a t , s t ) A_{\pi_{\theta_{now}}}(a_t,s_t) Aπθnow(at,st)。目前比较常用的方法是
广义优势估计(Generalized Advantage Estimation,GAE),先简介一下 GAE首先将 TD Error 表示为 δ t = r t + γ V ( s t + 1 ) − V ( s t ) \delta_t = r_t + \gamma V(s_{t+1})-V(s_t) δt=rt+γV(st+1)−V(st),其中 V V V 是一个已经学习的状态价值函数,根据多步 TD 思想有
A t ( 1 ) = δ t = − V ( s t ) + r t + γ V ( s t + 1 ) A t ( 2 ) = δ t + γ δ t + 1 = − V ( s t ) + r t + γ r t + 1 + γ 2 V ( s t + 2 ) A t ( 3 ) = δ t + γ δ t + 1 + γ 2 δ t + 2 = − V ( s t ) + r t + γ r t + 1 + γ 2 r t + 2 + γ 3 V ( s t + 3 ) ⋮ ⋮ A t ( k ) = ∑ l = 0 k − 1 γ l δ t + l = − V ( s t ) + r t + γ r t + 1 + … + γ k − 1 r t + k − 1 + γ k V ( s t + k ) \begin{array}{ll} A_{t}^{(1)}=\delta_{t} & =-V\left(s_{t}\right)+r_{t}+\gamma V\left(s_{t+1}\right) \\ A_{t}^{(2)}=\delta_{t}+\gamma \delta_{t+1} & =-V\left(s_{t}\right)+r_{t}+\gamma r_{t+1}+\gamma^{2} V\left(s_{t+2}\right) \\ A_{t}^{(3)}=\delta_{t}+\gamma \delta_{t+1}+\gamma^{2} \delta_{t+2} & =-V\left(s_{t}\right)+r_{t}+\gamma r_{t+1}+\gamma^{2} r_{t+2}+\gamma^{3} V\left(s_{t+3}\right) \\ \vdots & \vdots \\ A_{t}^{(k)}=\sum_{l=0}^{k-1} \gamma^{l} \delta_{t+l} & =-V\left(s_{t}\right)+r_{t}+\gamma r_{t+1}+\ldots+\gamma^{k-1} r_{t+k-1}+\gamma^{k} V\left(s_{t+k}\right) \end{array} At(1)=δtAt(2)=δt+γδt+1At(3)=δt+γδt+1+γ2δt+2⋮At(k)=∑l=0k−1γlδt+l=−V(st)+rt+γV(st+1)=−V(st)+rt+γrt+1+γ2V(st+2)=−V(st)+rt+γrt+1+γ2rt+2+γ3V(st+3)⋮=−V(st)+rt+γrt+1+…+γk−1rt+k−1+γkV(st+k) GAE 将这些不同步数的优势估计进行指数加权平均:
A t G A E = ( 1 − λ ) ( A t ( 1 ) + λ A t ( 2 ) + λ 2 A t ( 3 ) + ⋯ ) = ( 1 − λ ) ( δ t + λ ( δ t + γ δ t + 1 ) + λ 2 ( δ t + γ δ t + 1 + γ 2 δ t + 2 ) + ⋯ ) = ( 1 − λ ) ( δ ( 1 + λ + λ 2 + ⋯ ) + γ δ t + 1 ( λ + λ 2 + λ 3 + ⋯ ) + γ 2 δ t + 2 ( λ 2 + λ 3 + λ 4 + … ) + ⋯ ) = ( 1 − λ ) ( δ t 1 1 − λ + γ δ t + 1 λ 1 − λ + γ 2 δ t + 2 λ 2 1 − λ + ⋯ ) = ∑ l = 0 ∞ ( γ λ ) l δ t + l \begin{aligned} A_{t}^{G A E} & =(1-\lambda)\left(A_{t}^{(1)}+\lambda A_{t}^{(2)}+\lambda^{2} A_{t}^{(3)}+\cdots\right) \\ & =(1-\lambda)\left(\delta_{t}+\lambda\left(\delta_{t}+\gamma \delta_{t+1}\right)+\lambda^{2}\left(\delta_{t}+\gamma \delta_{t+1}+\gamma^{2} \delta_{t+2}\right)+\cdots\right) \\ & =(1-\lambda)\left(\delta\left(1+\lambda+\lambda^{2}+\cdots\right)+\gamma \delta_{t+1}\left(\lambda+\lambda^{2}+\lambda^{3}+\cdots\right)+\gamma^{2} \delta_{t+2}\left(\lambda^{2}+\lambda^{3}+\lambda^{4}+\ldots\right)+\cdots\right) \\ & =(1-\lambda)\left(\delta_{t} \frac{1}{1-\lambda}+\gamma \delta_{t+1} \frac{\lambda}{1-\lambda}+\gamma^{2} \delta_{t+2} \frac{\lambda^{2}}{1-\lambda}+\cdots\right) \\ & =\sum_{l=0}^{\infty}(\gamma \lambda)^{l} \delta_{t+l} \end{aligned} AtGAE=(1−λ)(At(1)+λAt(2)+λ2At(3)+⋯)=(1−λ)(δt+λ(δt+γδt+1)+λ2(δt+γδt+1+γ2δt+2)+⋯)=(1−λ)(δ(1+λ+λ2+⋯)+γδt+1(λ+λ2+λ3+⋯)+γ2δt+2(λ2+λ3+λ4+…)+⋯)=(1−λ)(δt1−λ1+γδt+11−λλ+γ2δt+21−λλ2+⋯)=l=0∑∞(γλ)lδt+l 其中, λ ∈ [ 0 , 1 ] \lambda \in[0,1] λ∈[0,1] 是在 GAE 中额外引入的一个超参数- λ = 0 \lambda=0 λ=0 时, A t G A E = δ t = r t + γ V ( s t + 1 ) − V ( s t ) A_{t}^{G A E} = \delta_t = r_t + \gamma V(s_{t+1})-V(s_t) AtGAE=δt=rt+γV(st+1)−V(st) 是仅仅只看一步差分得到的优势
- λ = 1 \lambda=1 λ=1 时, A t G A E = ∑ l = 0 ∞ γ l δ t + l = ∑ l = 0 ∞ γ l r t + l − V ( s t ) A_{t}^{G A E}=\sum_{l=0}^{\infty} \gamma^{l} \delta_{t+l}=\sum_{l=0}^{\infty} \gamma^{l} r_{t+l}-V\left(s_{t}\right) AtGAE=∑l=0∞γlδt+l=∑l=0∞γlrt+l−V(st) 是看每一步差分得到优势的完全平均值。
利用 GAE 估计优势函数 A π θ n o w ( a t , s t ) A_{\pi_{\theta_{now}}}(a_t,s_t) Aπθnow(at,st) 时,需要计算 π n o w \pi_{now} πnow 交互得到的轨迹每个 timestep的 TD error δ t \delta_t δt,为此需要引入价值网络(critic)来估计 V θ n o w V_{\theta_{now}} Vθnow,得到所有 δ t \delta_t δt 后直接代入 GAE 公式 A t G A E = ∑ l = 0 ∞ ( γ λ ) l δ t + l A_{t}^{G A E}=\sum_{l=0}^{\infty}(\gamma \lambda)^{l} \delta_{t+l} AtGAE=∑l=0∞(γλ)lδt+l 即可
-
2.1.2 最大化
- 最大化这一步是 PPO 和 TPRO 唯一的区别,首先二者的置信域约束优化问题均可表示为
max θ E S ∼ d π θ n o w E A ∼ π θ n o w ( ⋅ ∣ S ) [ π θ ( A ∣ S ) π θ n o w ( A ∣ S ) ⋅ A π θ n o w ( S , A ) ] s.t. E S ∼ d π θ n o w D KL [ π θ n o w ( ⋅ ∣ S ) ∣ ∣ π θ ( ⋅ ∣ S ) ] ≤ △ \begin{aligned} &\max_\theta &&\mathbb{E}_{S\sim d^{\pi_{{\theta_{now}}}}}\mathbb{E}_{A\sim\pi_{\theta_{now}}(·|S)}\left[\frac{ \pi_{\theta}(A|S) }{\pi_{\theta_{now}}(A|S)}\cdot A_{\pi_{\theta_{now}}}(S,A)\right] \\ &\text{s.t.} &&\mathbb{E}_{S\sim d^{\pi_{\theta_{now}}}} D_\text{KL}\big[\pi_{\theta_{now}}(·|S) || \pi_{\theta}(·|S) \big] \leq \triangle \end{aligned} θmaxs.t.ES∼dπθnowEA∼πθnow(⋅∣S)[πθnow(A∣S)πθ(A∣S)⋅Aπθnow(S,A)]ES∼dπθnowDKL[πθnow(⋅∣S)∣∣πθ(⋅∣S)]≤△- TRPO 使用泰勒展开近似、共轭梯度、线性搜索等方法直接求解约束优化问题
- PPO 使用拉格朗日乘子法、限制目标函数等方式去除约束,然后就可以直接用梯度下降简单地求解无约束最优化问题
- 具体来说,PPO 有两种形式,一是 PPO-惩罚,二是 PPO-截断,我们接下来对这两种形式进行介绍:
PPO-惩罚:用拉格朗日乘数法直接将 KL 散度的限制放进了目标函数中,将原问题转换为无约束优化问题。迭代过程中根据真实的 KL 散度值(约束效果)不断更新 KL 散度前的拉格朗日乘数(调节约束强度)。第 k k k 轮优化函数为:
arg max θ E S ∼ d π θ k E A ∼ π θ k ( ⋅ ∣ S ) [ π θ ( A ∣ S ) π θ k ( A ∣ S ) ⋅ A π θ k ( S , A ) − β D KL [ π θ k ( ⋅ ∣ S ) ∣ ∣ π θ ( ⋅ ∣ S ) ] ] \argmax_\theta \mathbb{E}_{S\sim d^{\pi_{{\theta_{k}}}}}\mathbb{E}_{A\sim\pi_{\theta_{k}}(·|S)}\left[\frac{ \pi_{\theta}(A|S) }{\pi_{\theta_{k}}(A|S)}\cdot A_{\pi_{\theta_{k}}}(S,A)-\beta D_\text{KL}\big[\pi_{\theta_{k}}(·|S) || \pi_{\theta}(·|S) \big] \right] θargmaxES∼dπθkEA∼πθk(⋅∣S)[πθk(A∣S)πθ(A∣S)⋅Aπθk(S,A)−βDKL[πθk(⋅∣S)∣∣πθ(⋅∣S)]] 令 d k = D KL [ π θ k ( ⋅ ∣ S ) ∣ ∣ π θ ( ⋅ ∣ S ) ] d_k = D_\text{KL}\big[\pi_{\theta_{k}}(·|S) || \pi_{\theta}(·|S) \big] dk=DKL[πθk(⋅∣S)∣∣πθ(⋅∣S)], β \beta β 的更新规则如下
β k + 1 = { β k 2 , d k < δ 1.5 2 β k , d k > 1.5 δ β k , o t h e r w i s e \beta_{k+1}=\left\{ \begin{aligned} \frac{\beta_k}{2}, && d_k < \frac{\delta}{1.5} \\ 2\beta_k, && d_k >1.5 \delta \\ \beta_k, && otherwise \end{aligned} \right. βk+1=⎩ ⎨ ⎧2βk,2βk,βk,dk<1.5δdk>1.5δotherwise 其中 δ \delta δ 是事先设定的一个超参数,用于限制学习策略和之前一轮策略的差距PPO-截断:直接在目标函数中进行限制,以保证新的参数和旧的参数的差距不会太大。第 k k k 轮优化函数为:
arg max θ E S ∼ d π θ k E A ∼ π θ k ( ⋅ ∣ S ) [ min ( π θ ( A ∣ S ) π θ θ k ( A ∣ S ) A π θ k ( S , A ) , clip ( π θ ( A ∣ S ) π θ k ( A ∣ S ) , 1 − ϵ , 1 + ϵ ) A π θ k ( S , A ) ) ] \underset{\theta}{\arg \max }\mathbb{E}_{S\sim d_{\pi_{{\theta_{k}}}}}\mathbb{E}_{A\sim\pi_{\theta_{k}}(·|S)}\left[\min \left(\frac{\pi_{\theta}(A \mid S)}{\pi_{\theta_{\theta_{k}}}(A \mid S)} A_{\pi_{\theta_{k}}}(S, A), \space\space\operatorname{clip}\left(\frac{\pi_{\theta}(A \mid S)}{\pi_{\theta_{k}}(A \mid S)}, 1-\epsilon, 1+\epsilon\right) A_{\pi_{\theta_{k}}}(S, A)\right)\right] θargmaxES∼dπθkEA∼πθk(⋅∣S)[min(πθθk(A∣S)πθ(A∣S)Aπθk(S,A), clip(πθk(A∣S)πθ(A∣S),1−ϵ,1+ϵ)Aπθk(S,A))] 其中 clip ( x , l , r ) : = max ( min ( x , r ) , l ) \text{clip}(x,l,r):=\max(\min(x,r),l) clip(x,l,r):=max(min(x,r),l),即把 x x x 限制在 [ l , r ] [l,r] [l,r] 内,上式中 ϵ \epsilon ϵ 是一个超参数,表示进行截断的范围。注意 min 操作中的两个选择,后者就是把前者 clip 到 [ 1 − ϵ , 1 + ϵ ] [1-\epsilon, 1+\epsilon] [1−ϵ,1+ϵ] 而已。直接将两个系数的曲线如下画出来
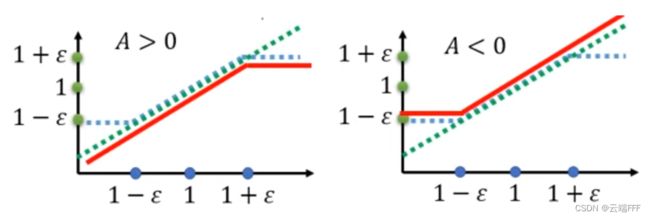
其中绿色虚线是 π θ ( A ∣ S ) π θ θ k ( A ∣ S ) \frac{\pi_{\theta}(A \mid S)}{\pi_{\theta_{\theta_{k}}}(A \mid S)} πθθk(A∣S)πθ(A∣S),蓝色虚线是 clip ( π θ ( A ∣ S ) π θ θ k ( A ∣ S ) , 1 − ε , 1 + ε ) \operatorname{clip}\big(\frac{\pi_{\theta}(A \mid S)}{\pi_{\theta_{\theta_{k}}}(A \mid S)}, 1-\varepsilon, 1+\varepsilon\big) clip(πθθk(A∣S)πθ(A∣S),1−ε,1+ε),红色实线是优势函数 A ( s t , a t ) A(s_t,a_t) A(st,at) 不同取值时 min \min min 操作选出的系数。以左图 A ( s , a ) > 0 A(s,a)>0 A(s,a)>0 的情况为例分析- A ( s , a ) > 0 A(s,a)>0 A(s,a)>0意味着状态 s s s 处动作 a a a 带来了好处,所以为了鼓励 a a a 出现系数应尽量大,但是不要超过 1 + ϵ 1+\epsilon 1+ϵ (就是说 s t s_t st 处选择 a t a_t at 的概率不要比现在高超过 1 + ϵ 1+\epsilon 1+ϵ 倍 ),以免策略网络出现 overstep
- 系数小于 1 时说明网络还处于欠拟合状态,并没有学到此时应在 s s s 位置鼓励选择动作 a a a,这时就不用限制了。所以注意到红色线有上限而无下限
- 大量实验表明,PPO-截断总是比 PPO-惩罚表现得更好
2.2 伪代码
2.3 用 PPO 方法解决 CartPole 问题
- 本节实验使用 gym 自带的 CartPole-V0 环境。这是一个经典的一阶倒立摆控制问题,agent 的任务是通过左右移动保持车上的杆竖直,若杆的倾斜度数过大,或者车子离初始位置左右的偏离程度过大,或者坚持时间到达 200 帧,则游戏结束

关于此环境动作状态空间、奖励函数及初始状态分布等的详细说明请参考 CartPole-V0 - 下面给出完整代码
import gym import torch import random import torch.nn.functional as F import numpy as np import matplotlib.pyplot as plt from tqdm import tqdm from gym.utils.env_checker import check_env from gym.wrappers import TimeLimit class PolicyNet(torch.nn.Module): ''' 策略网络是一个两层 MLP ''' def __init__(self, input_dim, hidden_dim, output_dim): super(PolicyNet, self).__init__() self.fc1 = torch.nn.Linear(input_dim, hidden_dim) self.fc2 = torch.nn.Linear(hidden_dim, output_dim) def forward(self, x): x = F.relu(self.fc1(x)) # (1, hidden_dim) x = F.softmax(self.fc2(x), dim=1) # (1, output_dim) return x class VNet(torch.nn.Module): ''' 价值网络是一个两层 MLP ''' def __init__(self, input_dim, hidden_dim): super(VNet, self).__init__() self.fc1 = torch.nn.Linear(input_dim, hidden_dim) self.fc2 = torch.nn.Linear(hidden_dim, 1) def forward(self, x): x = F.relu(self.fc1(x)) x = self.fc2(x) return x class PPO(torch.nn.Module): def __init__(self, state_dim, hidden_dim, action_range, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device): super().__init__() self.actor = PolicyNet(state_dim, hidden_dim, action_range).to(device) self.critic = VNet(state_dim, hidden_dim).to(device) self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr) self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr) self.device = device self.gamma = gamma self.lmbda = lmbda # GAE 参数 self.epochs = epochs # 一条轨迹数据用来训练的轮数 self.eps = eps # PPO 中截断范围的参数 self.device = device def take_action(self, state): state = torch.tensor(state, dtype=torch.float).to(self.device) state = state.unsqueeze(0) probs = self.actor(state) action_dist = torch.distributions.Categorical(probs) action = action_dist.sample() return action.item() def compute_advantage(self, gamma, lmbda, td_delta): ''' 广义优势估计 GAE ''' td_delta = td_delta.detach().numpy() advantage_list = [] advantage = 0.0 for delta in td_delta[::-1]: advantage = gamma * lmbda * advantage + delta advantage_list.append(advantage) advantage_list.reverse() return torch.tensor(np.array(advantage_list), dtype=torch.float) def update(self, transition_dict): states = torch.tensor(np.array(transition_dict['states']), dtype=torch.float).to(self.device) actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device) rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device) next_states = torch.tensor(np.array(transition_dict['next_states']), dtype=torch.float).to(self.device) dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device) td_target = rewards + self.gamma * self.critic(next_states) * (1-dones) td_delta = td_target - self.critic(states) advantage = self.compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device) old_log_probs = torch.log(self.actor(states).gather(1, actions)).detach() # 用刚采集的一条轨迹数据训练 epochs 轮 for _ in range(self.epochs): log_probs = torch.log(self.actor(states).gather(1, actions)) ratio = torch.exp(log_probs - old_log_probs) surr1 = ratio * advantage surr2 = torch.clamp(ratio, 1 - self.eps, 1 + self.eps) * advantage # 截断 actor_loss = torch.mean(-torch.min(surr1, surr2)) # PPO损失函数 critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach())) # 更新网络参数 self.actor_optimizer.zero_grad() self.critic_optimizer.zero_grad() actor_loss.backward() critic_loss.backward() self.actor_optimizer.step() self.critic_optimizer.step() if __name__ == "__main__": def moving_average(a, window_size): ''' 生成序列 a 的滑动平均序列 ''' cumulative_sum = np.cumsum(np.insert(a, 0, 0)) middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size r = np.arange(1, window_size-1, 2) begin = np.cumsum(a[:window_size-1])[::2] / r end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1] return np.concatenate((begin, middle, end)) def set_seed(env, seed=42): ''' 设置随机种子 ''' env.action_space.seed(seed) env.reset(seed=seed) random.seed(seed) np.random.seed(seed) torch.manual_seed(seed) state_dim = 4 # 环境观测维度 action_range = 2 # 环境动作空间大小 actor_lr = 1e-3 critic_lr = 1e-2 num_episodes = 500 hidden_dim = 128 gamma = 0.98 lmbda = 0.95 epochs = 10 eps = 0.2 device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu") # build environment env_name = 'CartPole-v0' env = gym.make(env_name, render_mode='rgb_array') check_env(env.unwrapped) # 检查环境是否符合 gym 规范 set_seed(env, 0) # build agent agent = PPO(state_dim, hidden_dim, action_range, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device) # start training return_list = [] for i in range(10): with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar: for i_episode in range(int(num_episodes / 10)): episode_return = 0 transition_dict = { 'states': [], 'actions': [], 'next_states': [], 'next_actions': [], 'rewards': [], 'dones': [] } state, _ = env.reset() # 以当前策略交互得到一条轨迹 while True: action = agent.take_action(state) next_state, reward, terminated, truncated, _ = env.step(action) next_action = agent.take_action(next_state) transition_dict['states'].append(state) transition_dict['actions'].append(action) transition_dict['next_states'].append(next_state) transition_dict['next_actions'].append(next_action) transition_dict['rewards'].append(reward) transition_dict['dones'].append(terminated or truncated) state = next_state episode_return += reward if terminated or truncated: break #env.render() # 用当前策略收集的数据进行 on-policy 更新 agent.update(transition_dict) # 更新进度条 return_list.append(episode_return) pbar.set_postfix({ 'episode': '%d' % (num_episodes / 10 * i + i_episode + 1), 'return': '%.3f' % episode_return, 'ave return': '%.3f' % np.mean(return_list[-10:]) }) pbar.update(1) # show policy performence mv_return_list = moving_average(return_list, 29) episodes_list = list(range(len(return_list))) plt.figure(figsize=(12,8)) plt.plot(episodes_list, return_list, label='raw', alpha=0.5) plt.plot(episodes_list, mv_return_list, label='moving ave') plt.xlabel('Episodes') plt.ylabel('Returns') plt.title(f'{agent._get_name()} on CartPole-V0') plt.legend() plt.savefig(f'./result/{agent._get_name()}.png') plt.show() - 收敛曲线如下所示
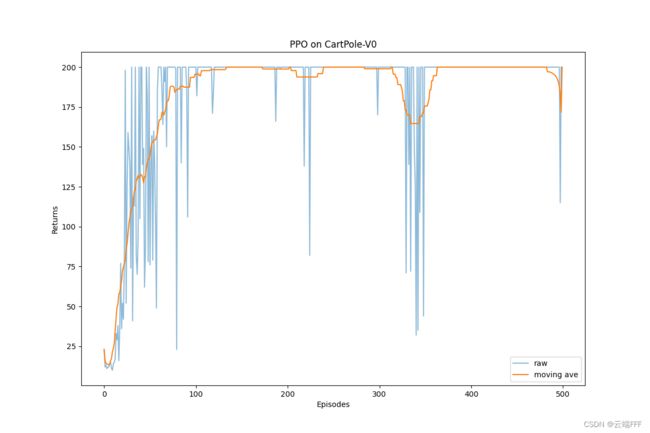
可见 PPO 的收敛速度和稳定性都比 前文 介绍的 REINFORCE with baseline 和 A2C 方法好得多
3. 总结
- 置信域策略优化(TRPO)是一种利用置信域算法优化策略的 On-policy Online RL 方法,它的优化目标和策略梯度方法相同,每次策略训练仅使用上一轮策略采样的数据,是 policy-based 类算法中十分有代表性的工作之一。直觉性地理解,TRPO 给出的观点是:由于策略的改变导致数据分布的改变,这大大影响深度模型实现的策略网络的学习效果,所以通过划定一个可信任的策略学习区域,保证策略学习的稳定性和有效性
- 近端策略优化 (PPO) 是 TRPO 的一种改进算法,它在实现上简化了 TRPO 中的复杂计算,并且它在实验中的性能大多数情况下会比 TRPO 更好,因此目前常被用作一种常用的基准算法。需要注意的是,TRPO 和 PPO 都属于在线策略学习算法,即使优化目标中包含重要性采样的过程,但其只是用到了上一轮策略的数据,而不是过去所有策略的数据