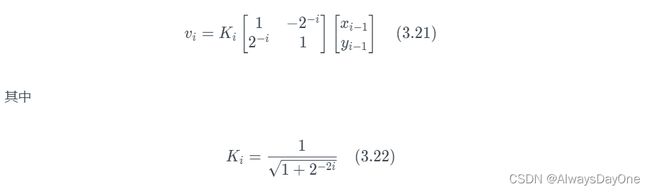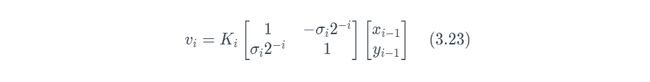HLS / Chisel 实现CORDIC算法计算三角函数（圆坐标系旋转模式）

CORDIC(坐标旋转数字算法)是一种计算三角、双曲和其他数学函数的有效方法。它是一种数字算法，每次运算均产生一次结果输出。这使我们能够根据应用需求调整算法精度；增加运算迭代次数可以得到更精确的结果。

CORDIC是只使用加法、减法、移位和查找表实现的简单算法，这种算法在FPGA中实现效率高，在硬件算法实现中经常用到。

CORDIC CR模式 原理

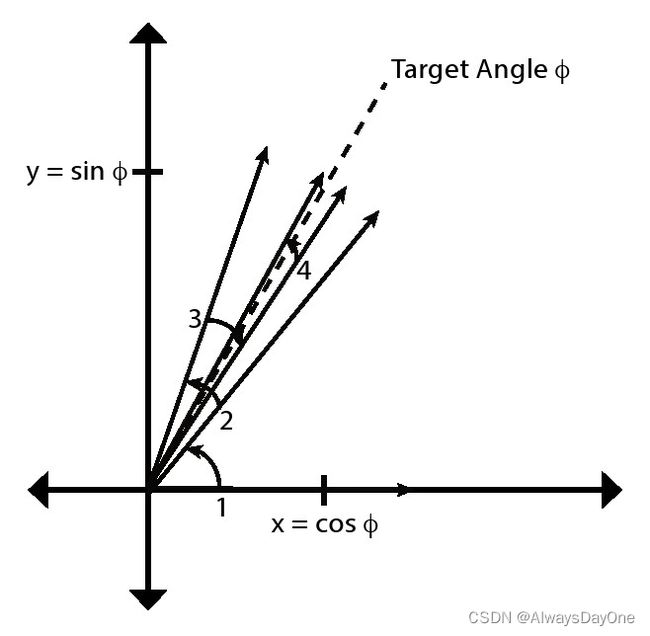
在这里，CORDIC算法从X轴正半轴开始，对应的角度为0度，然后执行四次或顺时针或逆时针的旋转，每次旋转的角度越来越小，最终得到目标角度φ。一旦旋转完成，得到的角度就与理论的角度十分接近了，如下图所示。如果我们假设向量的长度为1，从(x,y) = (1,0)即0°角开始，那么最终向量在x,y的分量就分别对应cosφ和sinφ。我们改善CORDIC算法的关键在于提升以上过程的计算效率。

• 在x轴上开始初始旋转矢量，即0°角。然后，我们执行一系列迭代旋转;在这个例子中，我们只执行四次旋转，但通常这是40次旋转。每个后续旋转使用越来越小的角度，这意味着每次迭代都会为输出值增加更多精度。在每次迭代中，我们决定以较小的角度进行正向或负向旋转。
• 我们旋转的角度值是先验固定的;因此，我们可以轻松地将它们的值存储在一个小内存中，并保持我们到目前为止已经旋转的累积角度的运行总和。
• 如果该累积角度大于我们的目标角度φ，则我们执行负旋转。如果它更小，那么旋转就是正的。
• 一旦我们完成了足够数量的旋转，我们就可以通过直接读取最终旋转矢量的x和y值来确定cosφ和sinφ

在二维中，旋转矩阵为：

$$R(\theta )=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$

在CORDIC的每次迭代中，我们执行以下操作来执行一次旋转，即矩阵向量乘法：

$$\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{x}_{i-1}\\ y_{i-1}\end{array}\right]=\left[\begin{array}{c}{x}_i\\ y_i\end{array}\right]$$

写出线性方程，新旋转矢量的坐标是：

$$x_i=x_{i-1}\cos \theta -y_{i-1}\sin \theta$$

$$y_i=x_{i-1}\sin \theta -y_{i-1}\cos \theta$$

如上可以发现还是有四个乘法在其中，对于实现硬件代价较高。

例如，可以考虑**乘以2的任意幂可以转变为移位操作。**如果我们将旋转矩阵中的常量设置为2的幂，我们可以非常容易地执行旋转而不需要乘法。

高效矩阵旋转

即只进行加/减和2的幂次乘法运算(即移位操作)。

再考虑旋转矩阵

如果我们限制tan(θi) 的值是2的幂次,那么旋转运算可以简化为数据移位（乘法）和加法。具体为,我们设tan(θi)=2^(−i) 。旋转矩阵就变成了

2^(−*i)*相当于数据向右移动i位，即等效于2的幂次除法。这基本上可以等效为一个简单的不需要任何资源的结构，在硬件实现上，它基本上是“无消耗”的.

但它也存在一些缺点。首先，我们受限只能旋转角度θ,其中tan(θi)=2^(−i) 。后续我们将证明这不是什么严重问题。第二，我们只展示了一个方向的旋转；而CORDIC要求能够旋转±θ,这个可以通过添加σ值（1或−1）来表示正向或者逆向旋转来修正这个错误。我们可能在每次迭代/旋转中有不同的σi 。因此旋转操作可概括为

$$x_i=K_i(x_{i-1}-{\sigma }_i{2}^{-i}{y}_{i-1})$$

$$y_i=K_i({\sigma }_i{2}^{-i}{x}_{i-1}+y_{i-1})$$

旋转矩阵需要乘以ki，在迭代过程中ki 通常被省略，然后在一系列旋转完成后进行补偿。比例因子累积为

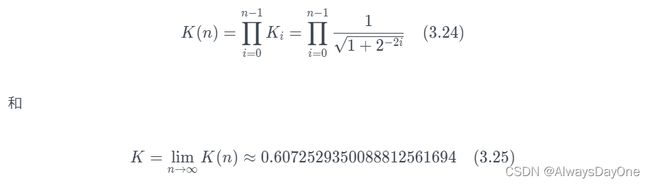
不同迭代的比例因子可以预先计算并存储。如果我们总是做固定次数的旋转，这个比例因子就是一个常数。

在每次迭代中,我们需要知道刚刚执行的旋转角θi。其中θi=arctan(2^−i)。我们可以提前计算每一个i对应的θi 值，然后把它们存储在片上内存中，之后我们可以像用查找表一样用这些值.

计算正弦和余弦

为了计算正弦和余弦值，我们从x轴正方向上的一个矢量开始(例如，初始角度45度)，然后执行一系列旋转直到我们逼近给定角θ。之后，我们可以直接读取旋转矢量的x和y值，这两个值即为对应cosθ和sinθ。这里假设最终矢量幅度等于1，你会看到计算正余弦并不难实现。

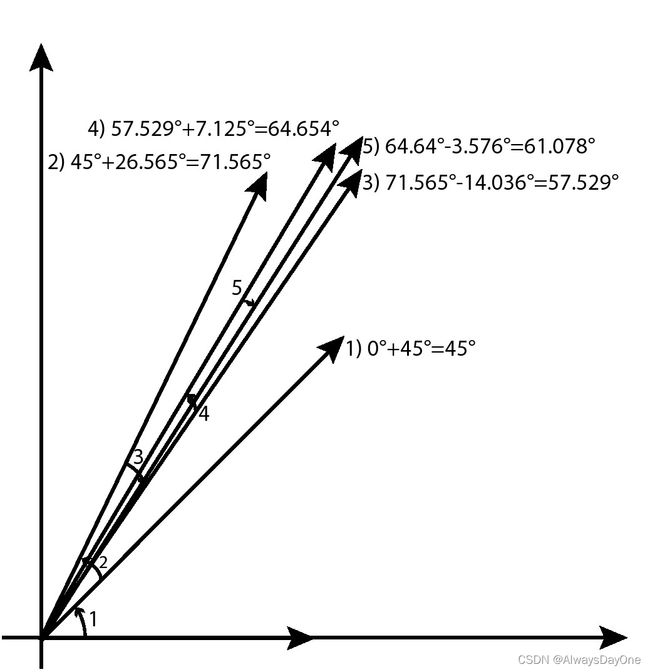
用CORDIC算法计算 cos60 和 sin60 。使用递增数i(0，1，2，3，4)来表示执行五次旋转，最终旋转结果为61.078度 。这个矢量对应的x和y值可以近似为指定角度的余弦和正弦值。

一般化CORDIC CR模式

如上对于计算sin cos的起始点为（1,0）点，若我们从任意一个（x,y）作为除法，那么基于其迭代公式最终起始实现了一个$\theta$角度的旋转
$$X=x\cos \theta -y\sin \theta$$
$$Y=x\sin \theta -y\cos \theta$$
输出(X,Y)即旋转后的角度，注意$\theta$值取值范围为[-90°，90°]

HLS代码思路

• 它将输入角作为目标角，输出这个角对应的正弦和余弦值
• 代码使用数组cordic_phase作为查找表，这个查找表存储每次迭代的旋转角度。
• 这个角度对应于表3.1中的“旋转角度”列中的值。
• 我们假设cordic.h文件定义不同的数据类型(例如,COS_SIN_TYPE和THETA_TYPE)并设置NUM_ITERATIONS为某个常数。
• 数据类型可以更改为不同的定点或浮点类型，设置NUM_ITERATIONS值要同时考虑我们期望的精度、资源和吞吐量。

#define THETA_TYPE float
#define COS_SIN_TYPE float
#define NUM_ITERATIONS 50

// The cordic_phase array holds the angle for the current rotation
// The data type of cordic & the iterations number of cordic
THETA_TYPE cordic_phase[] = {
    45.0, 26.565051177077986, 14.036243467926479, 7.125016348901799, 3.5763343749973515, 
        1.7899106082460694, 0.8951737102110744, 0.4476141708605531, 0.22381050036853808, 
        0.1119056770662069, 0.05595289189380367, 0.02797645261700368, 0.013988227142265015, 
        0.006994113675352919, 0.003497056850704011, 0.0017485284269804495, 0.0008742642136937803, 
        0.00043713210687233457, 0.00021856605343934782, 0.00010928302672007149, 5.464151336008544e-05, 
        2.732075668004893e-05, 1.3660378340025243e-05, 6.830189170012718e-06, 3.4150945850063712e-06, 
        1.7075472925031871e-06, 8.537736462515938e-07, 4.2688682312579694e-07, 2.1344341156289847e-07, 
        1.0672170578144923e-07, 5.336085289072462e-08, 2.668042644536231e-08, 1.3340213222681154e-08, 
        6.670106611340577e-09, 3.3350533056702886e-09, 1.6675266528351443e-09, 8.337633264175721e-10, 
        4.1688166320878607e-10, 2.0844083160439303e-10, 1.0422041580219652e-10, 5.211020790109826e-11, 
        2.605510395054913e-11, 1.3027551975274565e-11, 6.513775987637282e-12, 3.256887993818641e-12, 
        1.6284439969093206e-12, 8.142219984546603e-13, 4.0711099922733015e-13, 2.0355549961366507e-13, 
        1.0177774980683254e-13, 5.088887490341627e-14, 2.5444437451708134e-14, 1.2722218725854067e-14, 
        6.3611093629270335e-15, 3.1805546814635168e-15, 1.5902773407317584e-15, 7.951386703658792e-16, 
        3.975693351829396e-16, 1.987846675914698e-16, 9.93923337957349e-17, 4.969616689786745e-17, 
        2.4848083448933725e-17, 1.2424041724466862e-17, 6.212020862233431e-18, 3.1060104311167156e-18, 
        1.5530052155583578e-18, 7.765026077791789e-19, 3.8825130388958945e-19, 1.9412565194479472e-19, 
        9.706282597239736e-20, 4.853141298619868e-20, 2.426570649309934e-20, 1.213285324654967e-20, 
        6.066426623274835e-21, 3.0332133116374176e-21, 1.5166066558187088e-21, 7.583033279093544e-22, 
        3.791516639546772e-22, 1.895758319773386e-22, 9.47879159886693e-23, 4.739395799433465e-23, 
        2.3696978997167325e-23, 1.1848489498583662e-23, 5.924244749291831e-24, 2.9621223746459156e-24, 
        1.4810611873229578e-24, 7.405305936614789e-25, 3.7026529683073945e-25, 1.8513264841536972e-25, 
        9.256632420768486e-26, 4.628316210384243e-26, 2.3141581051921216e-26, 1.1570790525960608e-26, 
        5.785395262980304e-27, 2.892697631490152e-27, 1.446348815745076e-27, 7.23174407872538e-28, 
        3.61587203936269e-28, 1.807936019681345e-28, 9.039680098406725e-29
};
// 在趋近于无穷大的时候，K值变为恒定
THETA_TYPE cordic_K = 0.6072529350088814

void cordic(COS_SIN_TYPE x = 1, COS_SIN_TYPE  y = 0, THETA_TYPE theta, COS_SIN_TYPE &s, COS_SIN_TYPE &c)
{
    // Set the initial vector that we wil rorate
    // current_cos = I; current = Q
    COS_SIN_TYPE current_cos = x;
    COS_SIN_TYPE current_sin = y;
    
    // Factor is the 2^(-L) value
    COS_SIN_TYPE factor = 1.0;
    
    // This loop iteratively rotates the initial vector to find the
    // sine and cosine vlaue corresponding to the input theta angle
    int j = 0；
    for(;j < NUM_ITERATIONS; j++){
        // Determine if we are rotating by a positive or negative angle
        int sigma = (theta < 0) ? -1 : 1;
        
        // Save ther current_cos, so that it can be used in the sine calculation
        COS_SIN_TYPE temp_cos = current_cos;
        
        // Perform ther roation
        current_cos = current_cos - current_sin * sigma * factor;
        current_sin = temp_cos * sigma * factor + current_sin;
        
        // Determin the new theta
        theta = theta - sigma * cordic_phase[j];
        
        // calculate newxt 2^(-L) value
        factor = factor >> 1;
    }
    
    // Set ther final sine and cosine values
    s = current_sin * cordic_K;
    c = current_cos * cordic_K;
}

优化

对于factor变量有关的乘法器，通过限制代码只工作在定点数下，我们可以用移位和加法操作来替代。

void cordic(COS_SIN_TYPE x = 1, COS_SIN_TYPE  y = 0, THETA_TYPE theta, COS_SIN_TYPE &s, COS_SIN_TYPE &c)
{
    COS_SIN_TYPE current_cos = x;
    COS_SIN_TYPE current_sin = y;
    
    for(int j = 0; j < NUM_ITERATIONS; j++) {
        COS_SIN_TYPE cos_shift = current_cos >> j;
        COS_SIN_TYPE sin_shift >> j;
        if(theta >=0 ){
            current_cos = current_cos - sin_shift;
            current_sin = current_sin + cos_shift;
            theta = theta - cordic_phase[j];
        } else {
            current_cos = current_cos + sin_shift;
            current_sin = current_cos - sin_shift;
            theta = theta + cordic_phase[j];
        }
    }
    s = current_sin;
    c = current_cos;
}

Chisel实现方案

在HLS的代码实现思路，chisel需要对整个硬件的结构、数据存储和时钟等进行设计规划。这里用触发器来存储每一次迭代层级的结果，然后形成迭代N次的N级流水；将旋转角度和迭代的因子事先存储在rom中。实现代码如下：

定点数定义

首先定义定点数，注意在chisel.experimental包里有定点数的类

import chisel3._
import chisel3.util._
import chisel3.experimental._
import scala.collection.immutable
import scala.math._

/* 定点数的位宽定义 */ 
trait HasDataConfig {
  val DataWidth = 24
  val BinaryPoint = 10
}

源码实现

然后实现cordic算法计算sin cos：

• 其中注意有调试的接口将每一级流水线的计算值输出

class CORDIC_SIN_COS_ORIGIN(NUM_ITERATIONS: Int = 20) extends Module with HasDataConfig {
  /*
   * @NUM_ITERATIONS : 输入的迭代次数 Int类型
   * @theta : 输入的角度，以°为单位 定点数类型 输入范围[-90°,90°]
   * @cos : 输出的余弦值 定点数类型
   * @sin : 输出的正弦值 定点数类型
   * details: 利用cordic圆坐标系的迭代得到三角函数的近似值，
               建议迭代次数不超过30，在25次时，K值的变化已经
               在超过了float的范围
  **/
  val io = IO(new Bundle {
    val theta: FixedPoint = Input(FixedPoint(DataWidth.W, BinaryPoint.BP))
    val sin: FixedPoint = Output(FixedPoint(DataWidth.W, BinaryPoint.BP))
    val cos: FixedPoint = Output(FixedPoint(DataWidth.W, BinaryPoint.BP))
    /* Debug */
//    val sin_o: Vec[FixedPoint] = Output(Vec(NUM_ITERATIONS, FixedPoint(DataWidth.W, BinaryPoint.BP)))
//    val cos_o: Vec[FixedPoint] = Output(Vec(NUM_ITERATIONS, FixedPoint(DataWidth.W, BinaryPoint.BP)))
//    val theta_o: Vec[FixedPoint] = Output(Vec(NUM_ITERATIONS, FixedPoint(DataWidth.W, BinaryPoint.BP)))
  })

  /* 旋转度数表 */
  val inits_cordic_phase: immutable.Seq[FixedPoint] = (0 until NUM_ITERATIONS).map(
    t => FixedPoint.fromDouble(atan(pow(2, -t).toDouble) / Pi * 180, DataWidth.W, BinaryPoint.BP))
  val cordic_phase: Vec[FixedPoint] = VecInit(inits_cordic_phase)

  /* 在趋近于无穷大的时候，K值变为恒定 */
  val cordic_K: FixedPoint = FixedPoint.fromDouble(0.6072529350088814, DataWidth.W, BinaryPoint.BP)

  /* 初始化计算的寄存器数组，形成NUM_ITERATIONS级流水 */
  val current_x: Vec[FixedPoint] = RegInit(VecInit(Seq.fill(NUM_ITERATIONS)(FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)))) // cos
  val current_y: Vec[FixedPoint] = RegInit(VecInit(Seq.fill(NUM_ITERATIONS)(FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)))) // sin
  val current_theta: Vec[FixedPoint] = RegInit(VecInit(Seq.fill(NUM_ITERATIONS)(FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)))) // 目标角度

  /* Factor is the 2^(-L) value */
  val factor_table: immutable.Seq[FixedPoint] = (0 until NUM_ITERATIONS).map(
    t => FixedPoint.fromDouble(pow(2, -t).toDouble, DataWidth.W, BinaryPoint.BP))

  for (i <- 0 until NUM_ITERATIONS) {
    val factor = factor_table(i)

    /*
     * x[i] = K(x[i-1] - sigma * 2^(-i) * y[i-1])
     * y[i] = K(y[i-1] + sigma * 2^(-i) * x[i-1])
    **/
    if (i == 0) {
      /* 流水线第一级直接对(1,0)点做运算 */
      current_x(i) := FixedPoint.fromDouble(1.0, DataWidth.W, BinaryPoint.BP) // - 0*factor
      when(io.theta < FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)) {
        current_y(i) := FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP) -
          FixedPoint.fromDouble(1.0, DataWidth.W, BinaryPoint.BP) * factor
        current_theta(i) := io.theta + cordic_phase(i)
      }.otherwise {
        current_y(i) := FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP) +
          FixedPoint.fromDouble(1.0, DataWidth.W, BinaryPoint.BP) * factor
        current_theta(i) := io.theta - cordic_phase(i)
      }
    } else {
      when(current_theta(i - 1) < FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)) {
        current_x(i) := current_x(i - 1) + current_y(i - 1) * factor
        current_y(i) := current_y(i - 1) - current_x(i - 1) * factor
        current_theta(i) := current_theta(i - 1) + cordic_phase(i)
      }.otherwise {
        current_x(i) := current_x(i - 1) - current_y(i - 1) * factor
        current_y(i) := current_y(i - 1) + current_x(i - 1) * factor
        current_theta(i) := current_theta(i - 1) - cordic_phase(i)
      }
    }

    /* Debug */
//    io.cos_o(i) := current_x(i)
//    io.sin_o(i) := current_y(i)
//    io.theta_o(i) := current_theta(i)
  }

  io.cos := current_x(NUM_ITERATIONS - 1) * cordic_K
  io.sin := current_y(NUM_ITERATIONS - 1) * cordic_K
}

优化

同样这里对于factor变量有关的乘法器，通过限制代码只工作在定点数下，我们可以用移位和加法操作来替代。

class CORDIC_SIN_COS_ORIGIN(NUM_ITERATIONS: Int = 20) extends Module with HasDataConfig {
  /*
   * @NUM_ITERATIONS : 输入的迭代次数 Int类型
   * @theta : 输入的角度，以°为单位 定点数类型 输入范围[-90°,90°]
   * @cos : 输出的余弦值 定点数类型
   * @sin : 输出的正弦值 定点数类型
   * details: 利用cordic圆坐标系的迭代得到三角函数的近似值，
               建议迭代次数不超过30，在25次时，K值的变化已经
               在超过了float的范围
  **/
  val io = IO(new Bundle {
    val theta: FixedPoint = Input(FixedPoint(DataWidth.W, BinaryPoint.BP))
    val sin: FixedPoint = Output(FixedPoint(DataWidth.W, BinaryPoint.BP))
    val cos: FixedPoint = Output(FixedPoint(DataWidth.W, BinaryPoint.BP))
    /* Debug */
//    val sin_o: Vec[FixedPoint] = Output(Vec(NUM_ITERATIONS, FixedPoint(DataWidth.W, BinaryPoint.BP)))
//    val cos_o: Vec[FixedPoint] = Output(Vec(NUM_ITERATIONS, FixedPoint(DataWidth.W, BinaryPoint.BP)))
//    val theta_o: Vec[FixedPoint] = Output(Vec(NUM_ITERATIONS, FixedPoint(DataWidth.W, BinaryPoint.BP)))
  })

  /* 旋转度数表 */
  val inits_cordic_phase: immutable.Seq[FixedPoint] = (0 until NUM_ITERATIONS).map(
    t => FixedPoint.fromDouble(atan(pow(2, -t).toDouble) / Pi * 180, DataWidth.W, BinaryPoint.BP))
  val cordic_phase: Vec[FixedPoint] = VecInit(inits_cordic_phase)

  /* 在趋近于无穷大的时候，K值变为恒定 */
  val cordic_K: FixedPoint = FixedPoint.fromDouble(0.6072529350088814, DataWidth.W, BinaryPoint.BP)

  /* 初始化计算的寄存器数组，形成NUM_ITERATIONS级流水 */
  val current_x: Vec[FixedPoint] = RegInit(VecInit(Seq.fill(NUM_ITERATIONS)(FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)))) // cos
  val current_y: Vec[FixedPoint] = RegInit(VecInit(Seq.fill(NUM_ITERATIONS)(FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)))) // sin
  val current_theta: Vec[FixedPoint] = RegInit(VecInit(Seq.fill(NUM_ITERATIONS)(FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)))) // 目标角度

  for (i <- 0 until NUM_ITERATIONS) {
    /*
     * x[i] = K(x[i-1] - sigma * 2^(-i) * y[i-1])
     * y[i] = K(y[i-1] + sigma * 2^(-i) * x[i-1])
    **/
    if (i == 0) {
      /* 流水线第一级直接对(1,0)点做运算 */
      current_x(i) := FixedPoint.fromDouble(1.0, DataWidth.W, BinaryPoint.BP) // - 0*factor
      when(io.theta < FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)) {
        current_y(i) := FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP) -
          FixedPoint.fromDouble(1.0, DataWidth.W, BinaryPoint.BP) //  * factor = 1
        current_theta(i) := io.theta + cordic_phase(i)
      }.otherwise {
        current_y(i) := FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP) +
          FixedPoint.fromDouble(1.0, DataWidth.W, BinaryPoint.BP) //  * factor = 1
        current_theta(i) := io.theta - cordic_phase(i)
      }
    } else {
      when(current_theta(i - 1) < FixedPoint.fromDouble(0.0, DataWidth.W, BinaryPoint.BP)) {
        current_x(i) := current_x(i - 1) + (current_y(i - 1) >> i) // 移位替代乘法
        current_y(i) := current_y(i - 1) - (current_x(i - 1) >> i)
        current_theta(i) := current_theta(i - 1) + cordic_phase(i)
      }.otherwise {
        current_x(i) := current_x(i - 1) - (current_y(i - 1) >> i)
        current_y(i) := current_y(i - 1) + (current_x(i - 1) >> i)
        current_theta(i) := current_theta(i - 1) - cordic_phase(i)
      }
    }

    /* Debug */
//    io.cos_o(i) := current_x(i)
//    io.sin_o(i) := current_y(i)
//    io.theta_o(i) := current_theta(i)
  }

  io.cos := current_x(NUM_ITERATIONS - 1) * cordic_K
  io.sin := current_y(NUM_ITERATIONS - 1) * cordic_K
}

封装

如上的计算注意到theta: 输入的角度，以°为单位 定点数类型 输入范围[-90°,90°]，这是由于2^(-i)次方得到的旋转角度求级数和无法达到360°的效果，所以我们在外部封装一层解决这个问题

class cordic_sin_cos(NUM_ITERATIONS: Int = 20) extends Module with HasDataConfig {
  /*
   * @NUM_ITERATIONS : 输入的迭代次数 Int类型
   * @theta : 输入的角度，以°为单位 定点数类型 输入范围[-360,360°]
   * @cos : 输出的余弦值 定点数类型
   * @sin : 输出的正弦值 定点数类型
   * details: 利用cordic圆坐标系的迭代得到三角函数的近似值，
               建议迭代次数不超过30，在25次时，K值的变化已经
               在超过了float的范围
  **/
  val io = IO(new Bundle{
    val theta: FixedPoint = Input(FixedPoint(DataWidth.W, BinaryPoint.BP))
    val sin: FixedPoint = Output(FixedPoint(DataWidth.W, BinaryPoint.BP))
    val cos: FixedPoint = Output(FixedPoint(DataWidth.W, BinaryPoint.BP))
  })

  /* 将度数映射到[-180,180]*/
  val temp_theta: FixedPoint = Wire(FixedPoint(DataWidth.W, BinaryPoint.BP))
  when(io.theta > FixedPoint.fromDouble(180,DataWidth.W, BinaryPoint.BP)){
    temp_theta := io.theta - FixedPoint.fromDouble(360,DataWidth.W, BinaryPoint.BP)
  }.elsewhen(io.theta < FixedPoint.fromDouble(-180,DataWidth.W, BinaryPoint.BP)){
    temp_theta := io.theta + FixedPoint.fromDouble(360,DataWidth.W, BinaryPoint.BP)
  }.otherwise{
    temp_theta := io.theta
  }

  /* 将度数映射到[-90,90]*/
  val sigma_cos: Bool = Wire(Bool()) // 1 表示正数， 0表示负数
  val real_theta: FixedPoint = Wire(FixedPoint(DataWidth.W, BinaryPoint.BP))
  when(temp_theta > FixedPoint.fromDouble(90,DataWidth.W, BinaryPoint.BP)
  ){
    sigma_cos := 0.B
    real_theta := FixedPoint.fromDouble(180,DataWidth.W, BinaryPoint.BP) - temp_theta
  }.elsewhen(temp_theta < FixedPoint.fromDouble(-90,DataWidth.W, BinaryPoint.BP)){
    sigma_cos := 0.B
    real_theta := FixedPoint.fromDouble(-180,DataWidth.W, BinaryPoint.BP) - temp_theta
  }.otherwise{
    sigma_cos := 1.B
    real_theta := temp_theta
  }

  val cordic_unit: CORDIC_SIN_COS_ORIGIN = Module(new CORDIC_SIN_COS_ORIGIN(NUM_ITERATIONS))
  cordic_unit.io.theta := real_theta
  io.sin := cordic_unit.io.sin
  when(sigma_cos){
    io.cos := cordic_unit.io.cos
  }.otherwise{
    io.cos := -cordic_unit.io.cos
  }
}

生成Verilog代码

运行查看一下verilog代码

object cordicApp extends App {
  println(getVerilogString(new cordic_sin_cos))
  (new chisel3.stage.ChiselStage).emitVerilog(new cordic_sin_cos(10))
}

定义伴生对象工厂方法

最后我们定义三个伴生对象工厂方法来方便直接调用函数，无需多加连线

/*
 * 定义这个类的伴生对象，并定义一个工厂方法来简化模块的例化和连线。
 * 注意定义了伴生对象后，无法对原类进行测试实例化
**/
object cordic_sin_cos extends HasDataConfig{
  def apply(theta: FixedPoint, NUM_ITERATIONS: Int = 20):(FixedPoint, FixedPoint) = {
    /*
     * @NUM_ITERATIONS : 输入的迭代次数 Int类型
     * @theta : 输入的角度，以°为单位 定点数类型 输入范围[-360,360°]
     * @return cos : 输出的余弦值 定点数类型
     * @return sin : 输出的正弦值 定点数类型
     * details: 利用cordic圆坐标系的迭代得到三角函数的近似值，
                 建议迭代次数不超过30，在25次时，K值的变化已经
                 在超过了float的范围
    **/ 
    val cordic_unit = Module(new cordic_sin_cos(NUM_ITERATIONS))
    cordic_unit.io.theta := theta
    (cordic_unit.io.sin, cordic_unit.io.cos)
    }
}
object cordic_sin extends HasDataConfig{
  def apply(theta: FixedPoint, NUM_ITERATIONS: Int = 20):FixedPoint = {
    /*
     * @NUM_ITERATIONS : 输入的迭代次数 Int类型
     * @theta : 输入的角度，以°为单位 定点数类型 输入范围[-360,360°]
     * @return sin : 输出的正弦值 定点数类型
     * details: 利用cordic圆坐标系的迭代得到三角函数的近似值，
                 建议迭代次数不超过30，在25次时，K值的变化已经
                 在超过了float的范围
    **/ 
    val (sin,cos) = cordic_sin_cos(theta, NUM_ITERATIONS)
    sin
  }
}
object cordic_cos extends HasDataConfig{
  def apply(theta: FixedPoint, NUM_ITERATIONS: Int = 20):FixedPoint = {
    /*
     * @NUM_ITERATIONS : 输入的迭代次数 Int类型
     * @theta : 输入的角度，以°为单位 定点数类型 输入范围[-360,360°]
     * @return cos : 输出的余弦值 定点数类型
     * details: 利用cordic圆坐标系的迭代得到三角函数的近似值，
                 建议迭代次数不超过30，在25次时，K值的变化已经
                 在超过了float的范围
    **/ 
    val (sin,cos) = cordic_sin_cos(theta, NUM_ITERATIONS)
    cos
  }
}