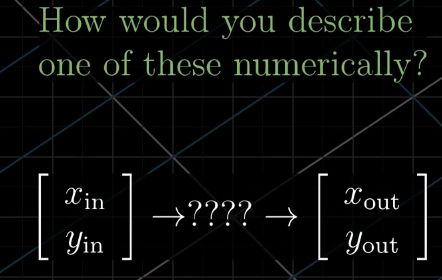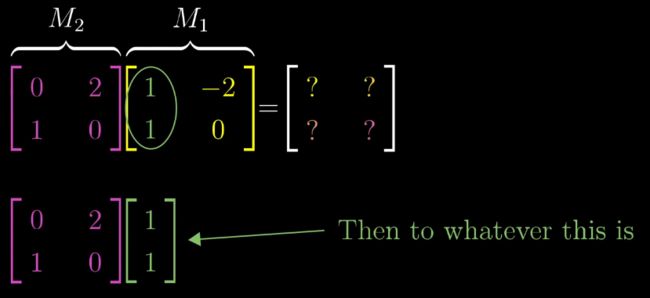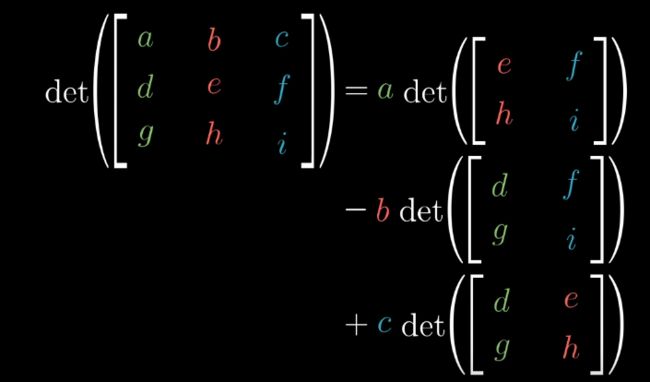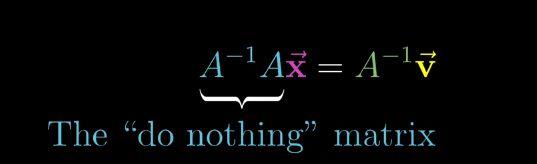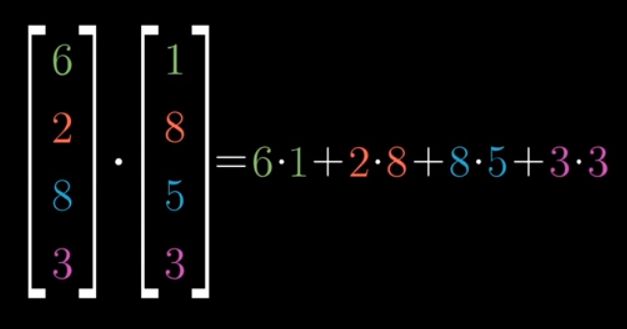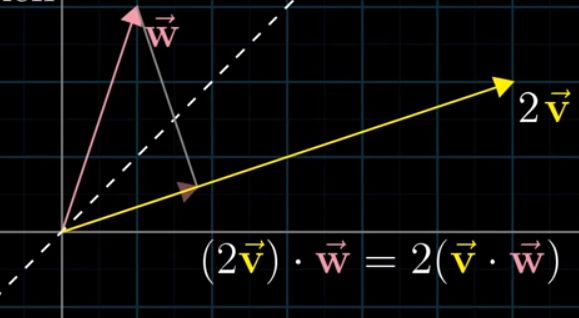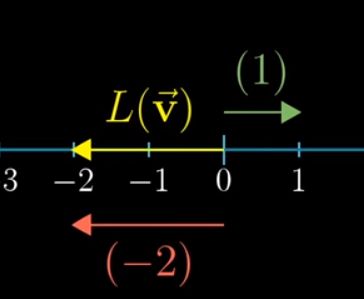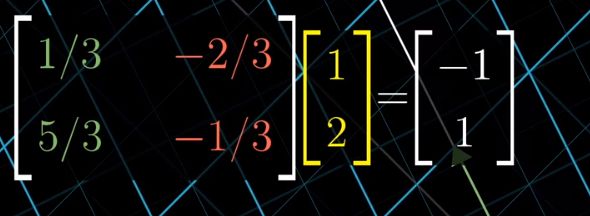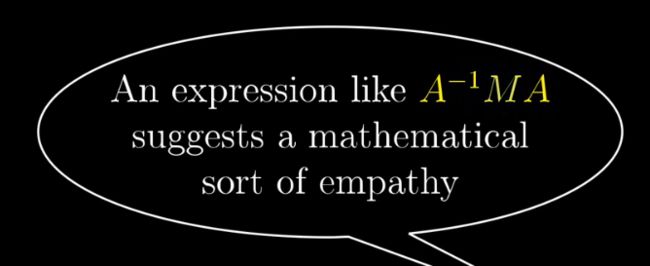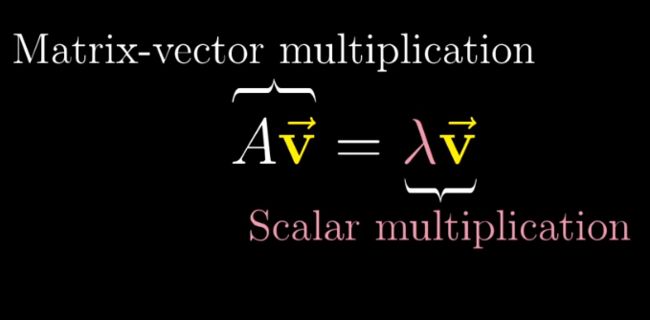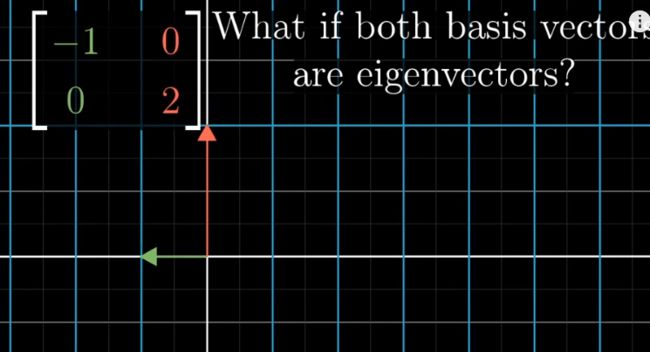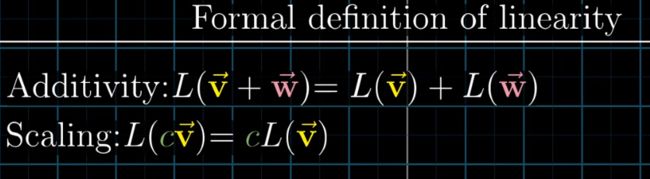3Blue1Brown:“线性代数的本质”完整笔记

我最早系统地学习线性代数是在大二时候，当时特意选修了学校物理系开设的4学分的线代，大概也就是比我们自己专业的线代多了一章向量空间的内容，其实最后上完发现，整个课程内容还是偏向于计算，对线性代数的几何直觉少有提起，对线性代数的实际运用更是鲜有涉及。同济的那本薄薄的如同九阴真经一般的教材，把线性代数讲的云里雾里，当时一个人在自习教室度过多少不眠之夜，一点一点去思考其概念定理背后的实际意义，多半也是边猜边想，苦不堪言。直到多年以后，有幸在网上听到了MIT的Strang老师开设的线代公开课，才对一些基础概念渐渐明朗，虽然至今又过去了很多年，但是对一些本质的理解，依然清晰。
不过，仔细想想，国内的教材写的云里雾里，才促使了我自发的思考，如果一切得来太容易，也许就不会那么刻骨铭心。我很早之前就想过这个问题，国内的教科书作者简直就是在下一盘大棋，自己出版的书写的高深莫测，翻译国外的书又翻译的含糊曲折，那么留给学生的只有两条路，要么去看原版的英语书，要么就是自己一点点看云雾缭绕的国产书，边猜边想边证明，不管走哪条路，都能走向成功。
最近，在youtube上看到了3Blue1Brown的Essence of linear algebra这门课，有种如获至宝的感觉，整个课程的时间并不长，但是对线性代数的讲解却十分到位，有种浓缩版的Gilbert Strang线代课程的感觉。希望通过这个课程，重温一下Linear Algebra。

Essence of linear algebra preview

• 线性代数使用场合

   

  

   

  讲师在课程中说道：许多学生学完了线代，会进行许多的计算，比如算行列式，算特征值，特征向量，算矩阵乘积，但是却不理解为什么矩阵的乘法这样定义，为什么cross product会和determinant(行列式)有关系，或者特征值究竟代表的是什么东西，其实这也是我当时学线代时候的疑问，书上并没有很明确的解释，也没有这样的视频课程来给你阐述，一切都是要靠自己去想。讲师指出，很多学生对这些概念背后的几何意义含糊不清，但是实际上，会进行线性代数的数值运算和真正在几何层面理解线性代数概念，完全不是一个level。几何意义的理解可以让你知道什么时候用什么数学工具来解决实际的问题，并且可以解释其结果的意义。当实计算结果这件事，交给计算机来做就行了。课堂上应该花大力气讲解概念，而不是计算，如果真的要讲计算，也应该是教会学生用matlab这样的工具。求逆矩阵，求代数余子式，求特征值什么的，还不是分分钟的事。

• 课程的目录

   

  

Vectors, what even are they?

• 向量的三种理解
  讲师上来就开门见山说道：The fundamental, root-of-it-all building block for linear algebra is the vector.
  向量是线性代数的基石（国外课程往往从向量开始说起，也就是从本质入手，国内则上来先定义逆序数，计算行列式，代数余子式，很容易把学生带偏），对向量的理解可以有三种角度：物理系学生的角度、计算机系学生的角度以及数学系学生的角度。
  物理系：向量是一个矢量（arrows pointing in space）, 或者说是一个在空间中有指向的箭头，定义这个向量，需要它的长度以及它指向的方向两个方面。在平面上的向量是二维的，在空间中的向量是三维的。
  计算机系：向量是ordered lists，并且在这些lists中存放的内容是numbers。
  数学系： a vector can be anything (-_-|||) 它们之间可以相加，相乘，也可以被数乘。

• 向量的几何意义
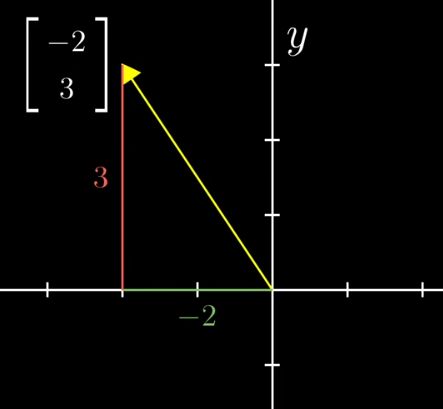
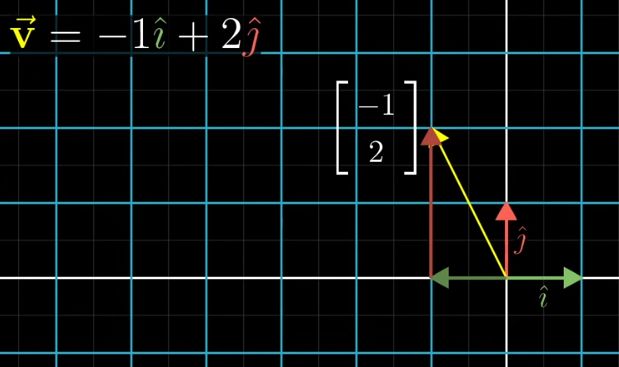
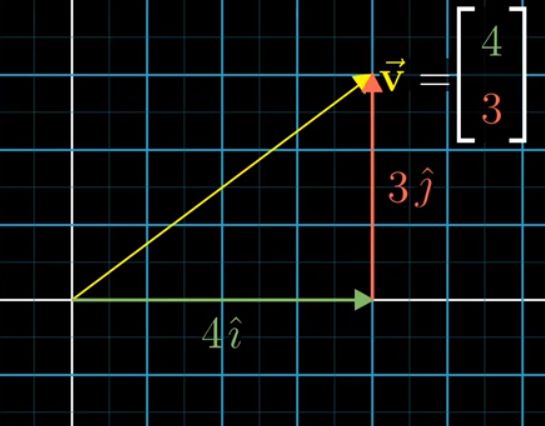
  不同于物理，在线代的领域里，把vector放在一个坐标系中，比如xy坐标系，其出发点在原点。

   

  

   

  比如这个向量，其数字的意义代表从该向量的起点（也就是原点）到终点分别在x轴和y轴上的距离，正负号代表方向。三维空间一样，只是多了一个Z轴。

• 向量加法的几何意义

   

  

   

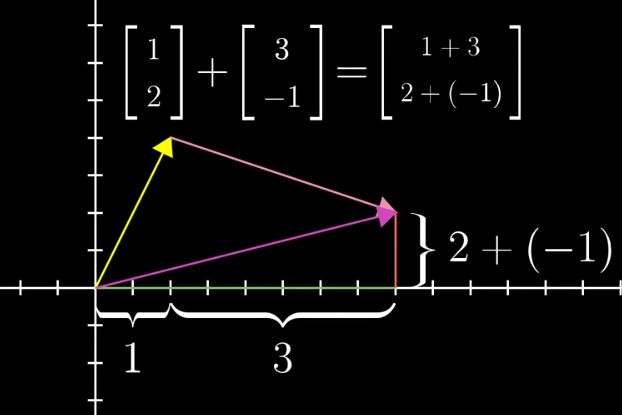
  三角形法则，好比有2只蚂蚁在一张纸上，第一只蚂蚁向上走2步向右走1步，然后再向下走1步，向右走3步。第2只蚂蚁直接向上走1步，向右走4步，就能和第一只蚂蚁站在相同的位置。也就是说第一只蚂蚁两次行动叠加之后所处的位置，和第二只蚂蚁一次行动是一致的。再进一步理解，其实要达到向右4步，向上1步的那个位置，有无数种走法，第一只蚂蚁的两次行动只是其中的一种分解。它也可以走10次走到那个位置。

   

  

• 向量乘法的几何意义

   

  

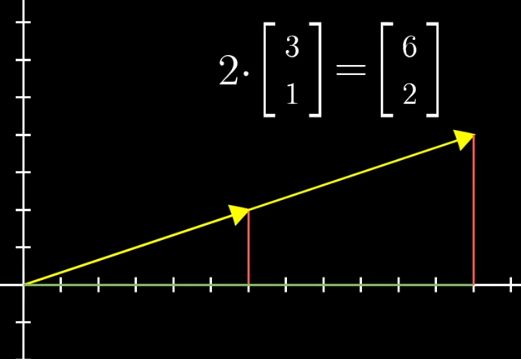
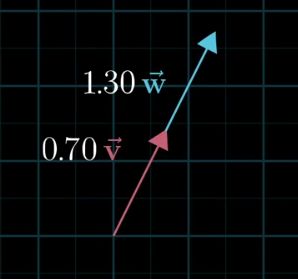
  乘以大于1的数值，就是将这个向量拉伸

   

  

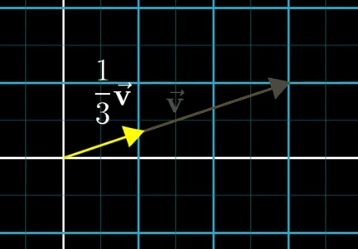
  乘以小于1的数值，就是将这个向量压缩

   

  

  乘以负数，就是将这个向量翻转

   

  拉伸，压缩，翻转向量的行为，统称为scaling，而这些数值本身，称之为scalars

   

  

   

  

Linear combinations, span, and basis vectors

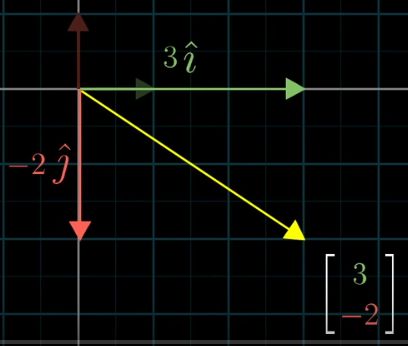
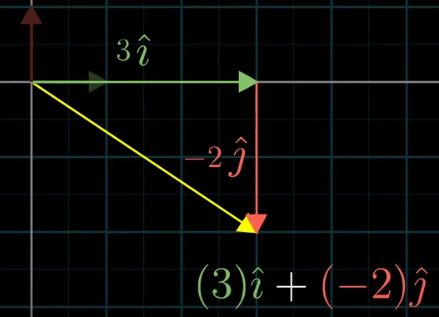
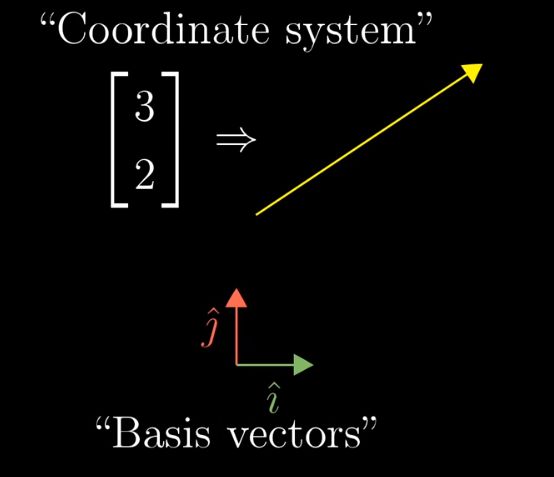
把这里的3和-2都看作是一个scalar，它们对原点的单位向量i和j进行scaling

于是，该(3,-2)向量就变成了两个scaling过的单位向量的和。

i和j是xy坐标系中的基础向量（basis vectors）

[其实也可以选择不同的basis vectors，比如说在平面上任意的两个向量作为基，这样得到的scalars的数值是不相同的，但是同样可以通过对这一对任意选择的basis vectors进行linear combination，而得到在平面上的任意向量。详见视频]

• 线性组合

  

  
  Linear Combination的几何意义如图所示，完整上来说，其实是向量之间的线性组合，其主体是向量，线性组合是一个操作，将各个向量scaling之后，相加在一起，就得到了参与操作的向量之间的一个Linear Combination。

• 线性组合的不同情况

   

  

  如果参与组合的一对向量不共线，那么由它们进行线性组合所得到的向量可以达到平面上的任意一个点

   

  

  如果参与组合的一对向量共线，那么由它们进行线性组合所得到的向量的终点被限制在一条通过原点的直线上

   

  

  如果参与组合的一对向量都是零向量，那么由它们进行线性组合所得到的向量永远是零向量

• span
  span : 是一组集合，它包含两个向量之间的全部线性组合

  

  
  如果你面对的是一组向量，那么考虑这些向量的坐标点。
  三维空间中，两个不共线的向量之间的span，也就是它们全部线性组合的集合，是一个由这两个向量所张成的平面。
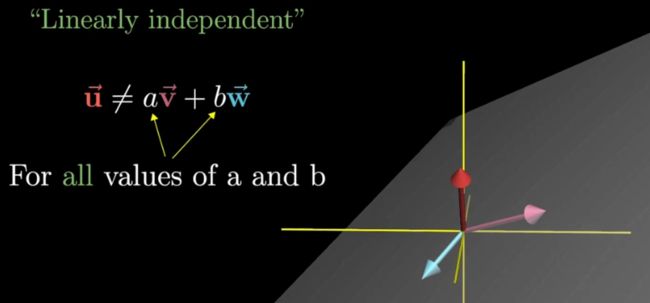
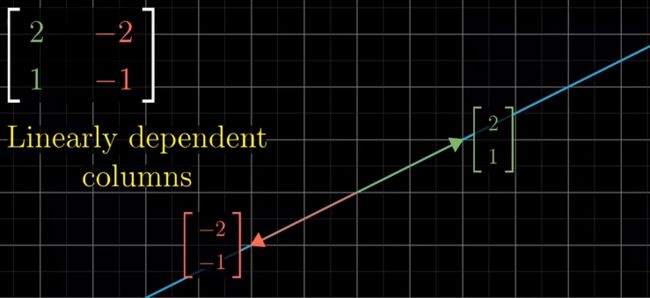
  如果在三维空间中，有3个向量，其中有2个共线，那么它们3者之间的线性组合所形成的set，只是三维空间中的一个平面，其中有一个向量是多余的(redundant)，因为span的set由两个向量便可以决定。而这两个共线的向量被称之为线性相关（Linearly dependent）

  线性无关（Linearly independent）的两个向量，不能通过scaling得到对方，其在平面上的几何意义是不共线

  

  二维空间的linearly independent

   

  

  三维空间的linearly independent

• basis的定义

The basis of a vector space is a set of linearly independent vectors that span the full spaces.
对于任意一个向量空间而言，它的基是一组相互之间线性独立的向量的集合，这些向量之间通过线性组合，可以span整个向量空间。

Linear transformations and matrices

• Linear transformations
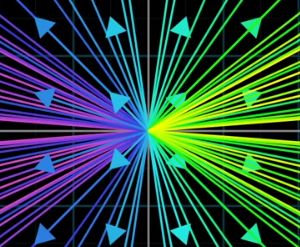
  讲师说道，transformations其实无非是function的fancy说法，本质上也是input和output，输入一个vector，经过某个transformation之后，得到一个输出的vector。整个过程，可以看作是输入的vector移动到了输出的vector的位置。考虑整个平面上的vector，在经过transformation之后，得到了一个最新的位置。

   

  

  input vectors

   

  

  output vectors

  如果用arrow来考虑的话，会比较杂乱，仅仅考虑每个向量的终点（起点必在原点），那么就变成了平面上点的集合，那么其效果就是原来的点移动到了新的位置。

   

  

  input vectors

   

  

  output vectors

• Linear transformations的两大特点

  经过变换之后：

  1. 所有的直线还是直线
  2. 原点还在原来的位置

• 描述Linear transformation

   

  

   

  给你一个输入的向量，如果表示????部分，从而得到你想要的输出的向量。

在做线性变换之前的V向量

在做线性变换之后的V向量

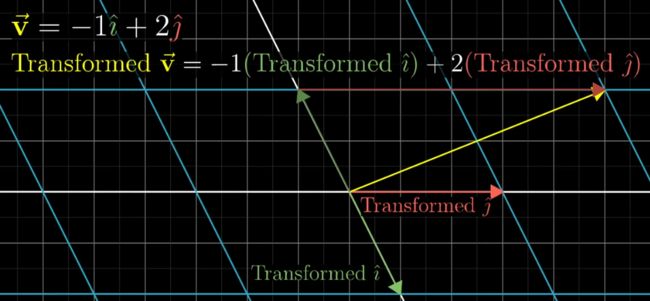
V向量在进行Linear Transformation之后，相当于-1倍的Transformed的i向量与2倍的Transformed的j向量之和，也就是说，在平面上，只需要记录i和j两个basis vectors的变化即可。

It started off as a certain linear combination of i-hat and j-hat and it ends up is that same linear combination of where those two vectors landed.
You can deduce where v must go based only on where i-hat and j-hat each landed.

保留了Linear Transformation之前的网格，可以看到i向量在transformed之后，落在了(1，-2)的位置，而j向量在transformed之后，则落在了(3,0)的位置

运算结果的几何意义

更进一步，该线性变换就是把原来的i（1,0）变化到（1，-2），把原来的j（0,1）变换到（3,0）。那么，原来平面上的每一个点（x,y），通过该变换，可以得到在平面上新的x和y的位置，新旧点之间一一对应

将这个变换提取成一个2*2的矩阵，第一列代表新i的位置，第二列代表新j的位置，新的i和j则是作为新的基

这样的话，如果有一个向量v（5,7），那么它经过通过图中的2*2矩阵描述的线性变换之后的向量，可以由如图示的运算所得到。其几何意义是变换后的i,j作为新的基，保持原来的scalars不变，对新的基进行线性组合

把它抽象化之后，则得到了矩阵乘法的运算公式，并且还可见其几何意义

假如transformed之后的向量是线性相关的，那么所有平面上的点在变换之后就被压缩到了一条直线上

These transformations can be described using only a handful of numbers.
These numbers are the coordinates of where each basis vectors lands.
Matrices give us a language to describe these transformations where the columns represent those coordinates.
Matrix-vector multiplication is just a way to compute what that transformation does to a given vector.
Every time you see a matrix, you can interpret it as a certain transformation of space.
Matrices as transformation of space.

Matrix multiplication as composition

• 组合变换概述
  组合变换，比如先进行一次rotation变换，再做一次sheer变换

   

  

  分步骤的变换矩阵

   

  

  该矩阵记录了这两次变换的总体效应

   

  

  两次分布变换的结果和一次组合变换的结果等效

   

  

   

  

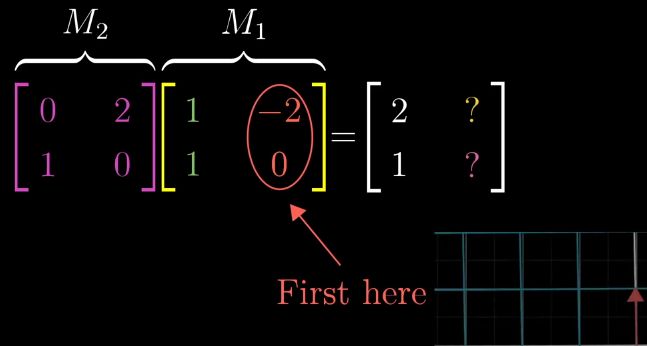
  先做的Rotation，再做的Shear，但是Rotation需要写在右边，右边的总是比左边的变换矩阵先操作

• 组合变换示例

   

  

  i向量一开始在M1的第一列向量

   

  

  接下来i向量被进行M2变换

   

  

  i向量在进行M2变换后落在了（2,1）位置

   

  

  两次变换后i的最终位置

   

  

  j向量的起始位置

   

  

  同理，j在变换后的位置

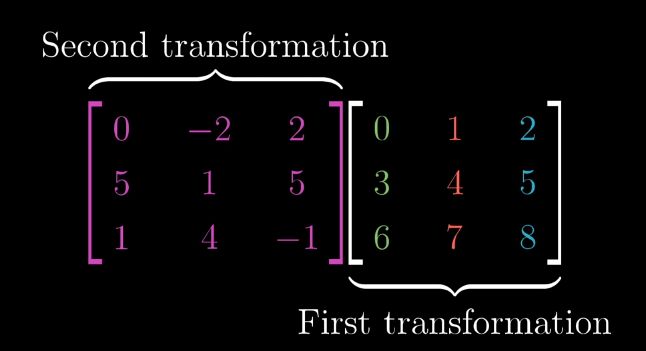
• 组合变换概括（矩阵乘法几何意义）

   

  

  抽象化之后

   

  

  最开始的i（e,g）经过M2变换之后，落到了（ae+bg,ce+dg）上

   

  

  最开始的j（f,h）经过M2变换之后，落到了（af+bh,cf+dh）上

   

  

  3维空间中的情况

   

  

  3维空间中的情况

The determinant

• 概述
  线性变换，有些是将原来的网格拉伸，有些是将原来的网格压缩，如果要定性的来描述变换，那么去测量拉伸或者压缩的程度不失为明智之举。

   

  

• 实例

   

  

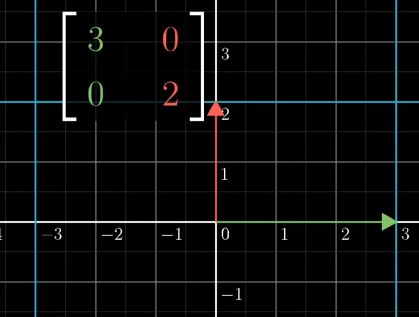
  变化前

   

  

  变化后

   

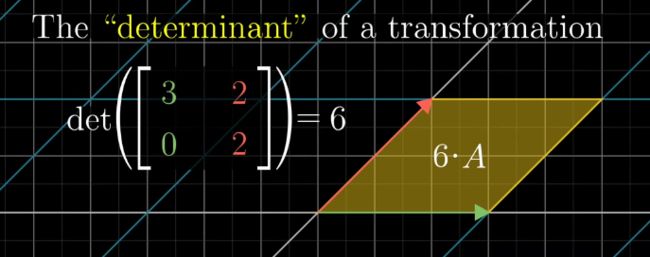
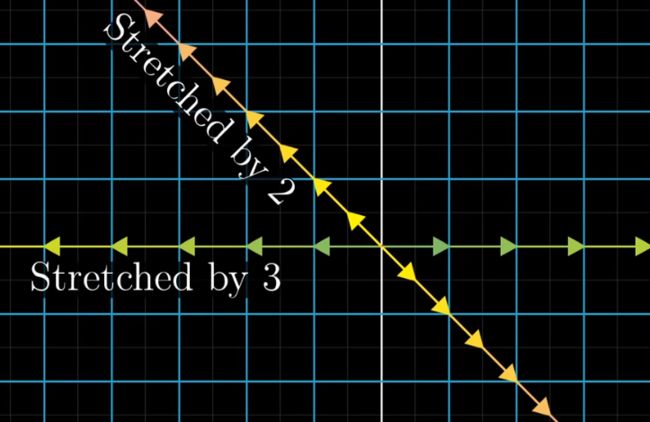
  可以看到，该变换将i拉伸了3倍，而将j拉伸了2倍

   

  

  变化之后i和j围成的方格的面积

   

  

  该线性变换将i和j原来围成的区域扩大了6倍

   

  

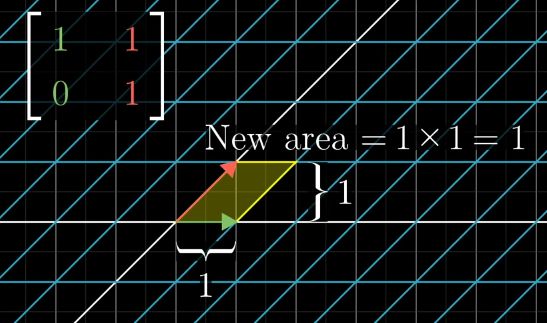
  shear变换之后，尽管网格形状改变，但是网格面积不变

• 定义

   

  

  determinant定量的描述出，在经过一个线性变换之后，原来单位向量所围成面积变化的倍数

   

  

  当determinant of a transformation的值为0的时候情况，只要检验某个Transformation的determinant的值是否为0，就可知该transformation是否把原来的空间压缩到更小的维度上

• determinant的正负含义——方向

   

  

   

  

  如果空间翻转的话，则determinant的值为负

   

  

  在三维空间中determinant of a transformation是体积的缩放

   

  

  在三维空间中determinant的正负号通过右手法则确定

• determinant的计算

   

  

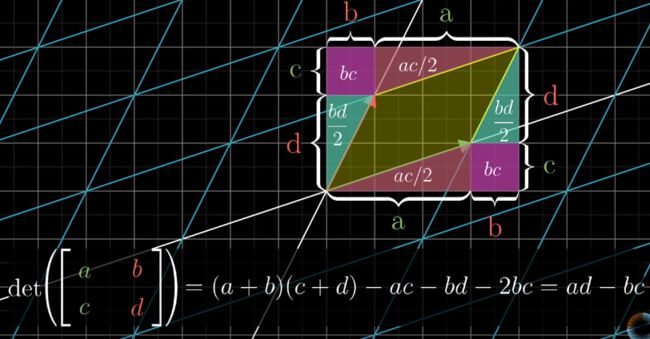
  二维空间的情况

   

  

  三维空间的情况

   

  

Inverse matrices, column space and null space

• 线性方程组

   

  

  coefficients,variables,constants

   

  

  constant matrix A, vector, constant vector

• Ax = v的几何意义

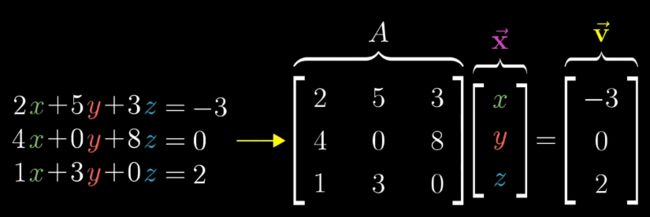
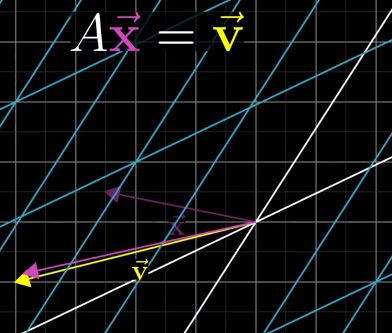
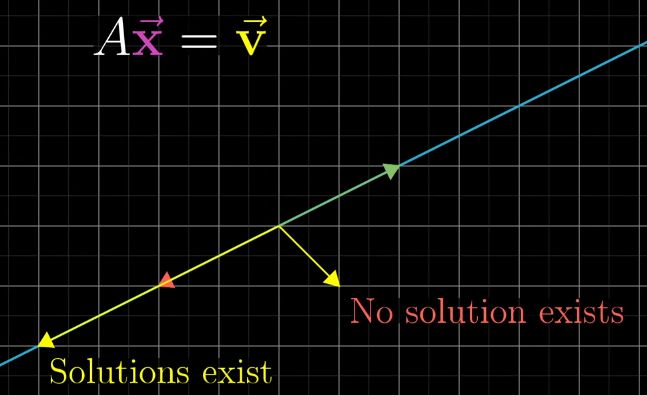
其中constant matrix A代表的是一种linear transformation,求解的过程，就是要找到这样一个向量x，使得向量x在经过A的linear transformation之后，和v向量重合。When the determinant of this transformation is not zero, it turns out that there will be one and only one vector that lands on v. 要找到这个解向量，可以像倒带一样，对v向量进行A的逆操作。

• 逆矩阵

   

  

  假如说A矩阵对某个向量进行了一次transformation，那么如果再进行A逆矩阵的transformation，则可以还原该向量的原始状态，从而抵消掉A对它的作用

比如说90度逆时针旋转这个transformation的逆操作就是顺时针旋转90度

determinant不为0，说明该变换不降维，A的逆矩阵存在

• Rank
  在三维空间中，如果全部input在某个Linear Transformation之后，全部output在一条直线上，那么这个transformation拥有rank 1。如果全部output在一个平面上，那么这个transformation拥有rank 2。对于1个2*2的矩阵而言，它的rank最多为2。

   

  

• 列空间

   

  

  image.png

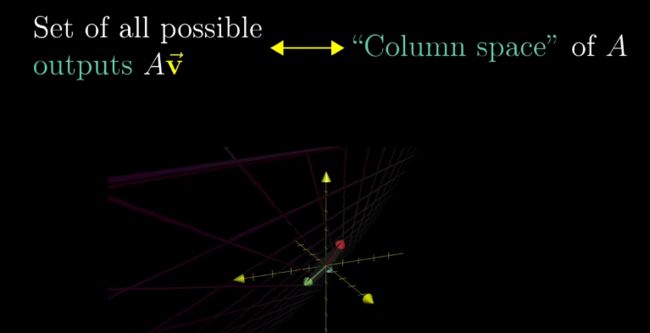
This set of all possible outputs for your matrix, whether it's a line, a plane, 3d space, whatever, is called the column space of your matrix.
注意，列空间的对象是矩阵，矩阵的意义是一个Linear Transformation的表示，某个Linear Transformation的所有outputs的集合，称之为该matrix的column space。

矩阵中的列向量，告诉你basis vectors所在的位置

而其列空间就是其basis vectors的span

column space: The column space is the span of the columns of your matrix.
rank: The number of dimensions in the column space.

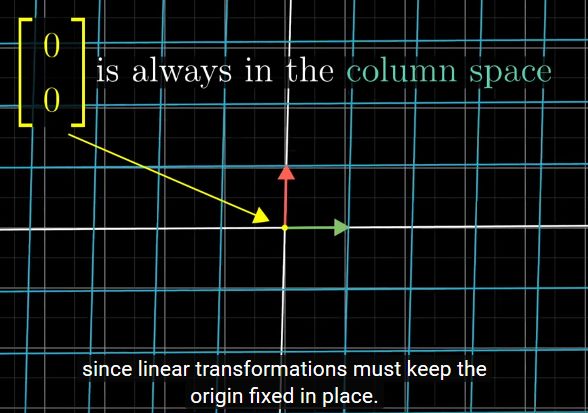
线性变换的原点位置不会改变，故0向量永远在列空间之中

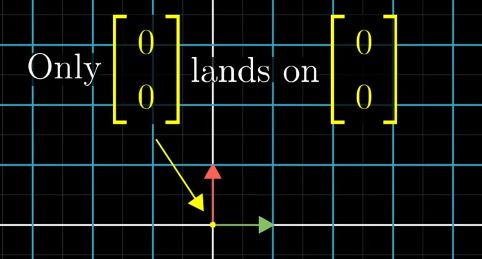
full rank的矩阵，唯一在变换后落在原点的只有零向量自身

• null space

   

  

  某一个3维的线性变换，将空间压缩到一条直线上，那么将会有一整个平面上的向量被变换到零向量的位置

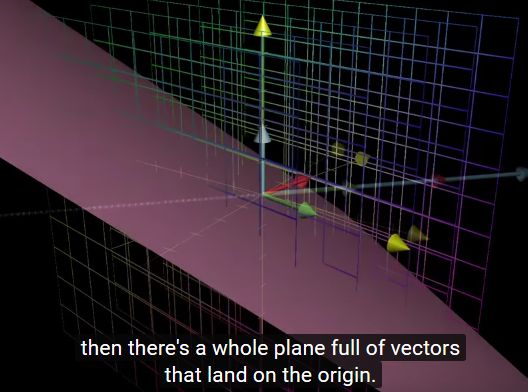
The set of vectors that lands on the origin is called the null space or the kernel of the Matrix.
如果某个向量空间在Linear Transformation之后，存在降维，那么就会有一系列原来不是零向量的向量落到了零向量的位置，所有这些向量的集合构成了null space

对线性方程组而言，当V正好是0向量的时候，则该矩阵A的零空间便包含了该线性方程组全部可能的解

可以通过列空间来判断对应的线性方程组是否有解

Nonsquare matrices as transformations between dimensions

• 概念

   

  

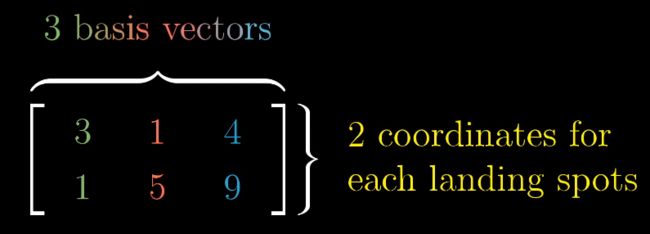
  非方阵体现了不同维数之间的变换

   

  

  此例中，i和j两个列向量的span（也就是列空间）是在三维空间中的一个平面，而这个矩阵依旧是full rank的

   

  

  行数代表的是列向量的维数，此例中，列向量是落在三维空间中的平面上的，这是一个从三维空间到二维空间的变换

Dot products and duality

• 基本运算

   

  

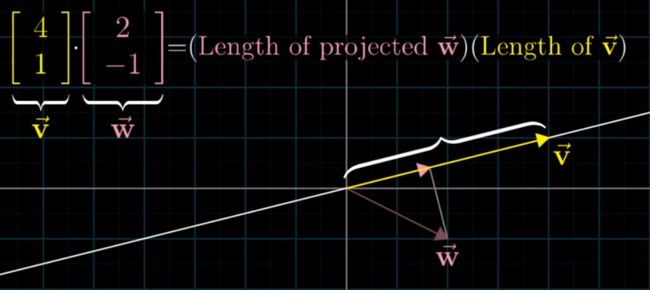
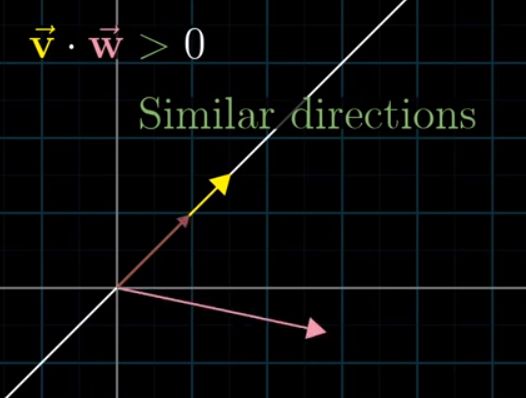
• 点积的几何意义

   

  

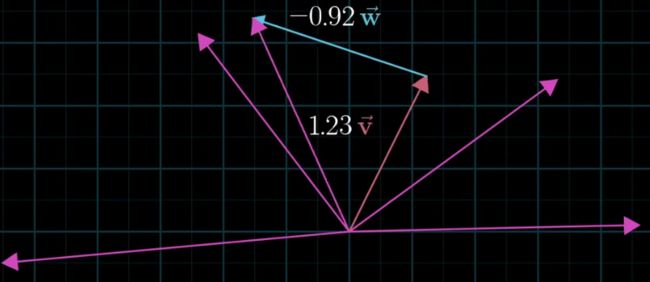
  把w投射到v所在的直线上，将w在v上投影的长度乘以v的长度，就是其点积的值

   

  

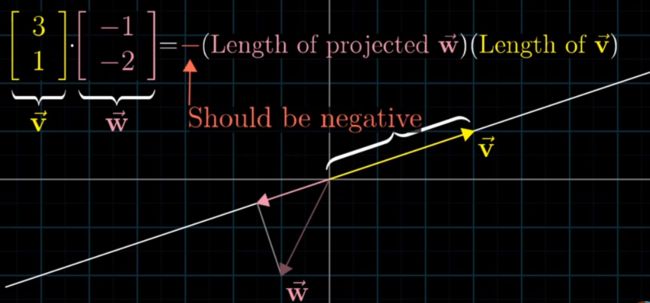
  如果w的投影和v的方向相反，则点积为负

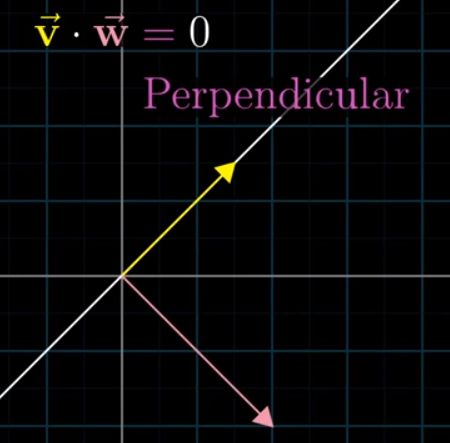
• 点积的几种情况

   

  

   

  

   

  

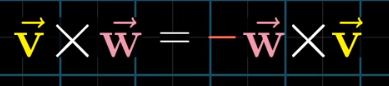
• 点积的结果和顺序无关

   

  

  v和w恰好相等的情况下

   

  

  如果v扩大了2倍，并不会改变w在v上投影的长度，因此等式直观成立，反之亦然

• Duality

Duality: Natural-but-surprising correspondence
the dual of a vector is the linear transformation that it encodes
the dual of a linear transformation from some space to one dimension is a certain vector in that space

假如说有一个线性变换，使得i落在1而j落在-2的位置

而被变换的向量v可以拆解成如图

基于Linearality，在变换之后，v是4倍的变换后的i，3倍变换后的j，由于在同一数轴上，合成后是-2

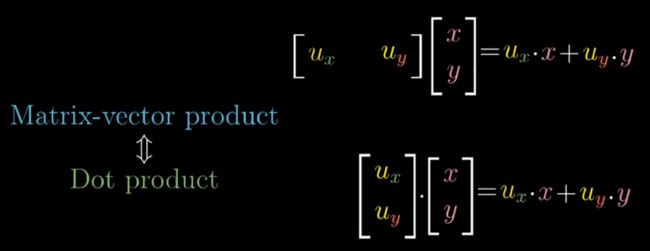
两个向量的点积的效果和一个向量进行降维transfrom一样

1*2的矩阵和2维向量之间存在关系，一个2d vector有其associated matrix，反之亦然。1*2的矩阵表示某个Linear Transformation，它能够将一个2维的vector变成1维的数字，而这个2维的vector本身是和这个矩阵所表示的Linear Transformation是相关联的

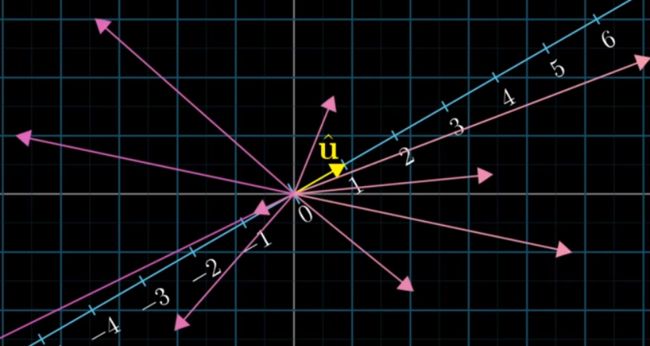
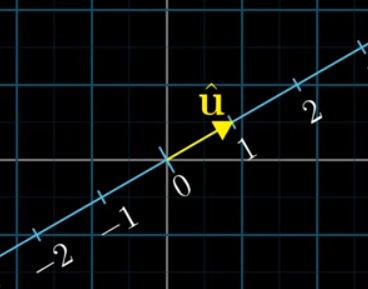
假设有一条相对于正坐标系倾斜的数轴，u落在其1坐标的位置

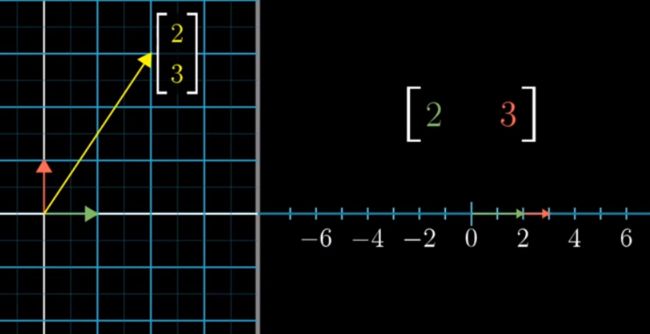
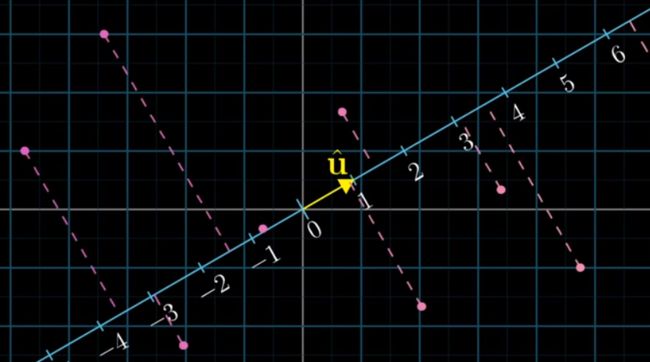
将正坐标系中的2维向量投射到这个数轴上

其实就相当于定义了一个从2维向量到1维数字的线性变换

u其实还是正坐标系中的一个2维向量，只是正好也落在了这个给定的倾斜数轴之上

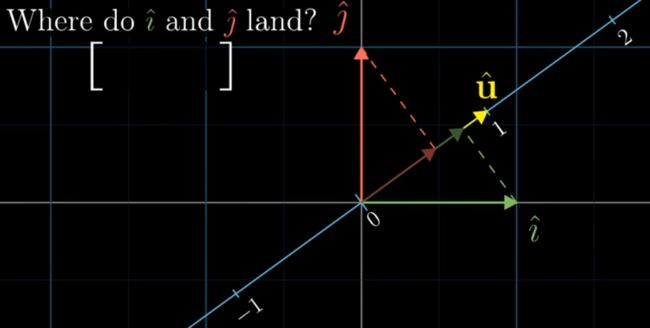
可以找到一个1*2的矩阵来描述这个线性变换

要找到这个矩阵，就是要看原来的i和j，在变换后落在了哪个位置，它们最后落点的位置，便是这个1*2矩阵的列

i和u都是单位向量，把i投射到u上，和把u投射到i上是对称的，j同理。那么，原来的i在u上投影后的落点，其实和u在正坐标系x轴上落点的数值是相同的，也就是u的横坐标

这样就建立起u这个向量和[ux uy]这个线性变换之间的关系。So the entries of the 1*2 matrix describing the projection transformation are going to be the coordinates of u-hat。u向量的坐标因为对偶性，和描述线性变换的1*2矩阵的两列是相等的

由于这样的关系，某一个向量和单位向量作点积运算的值，可以解释成将该向量投影到单位向量所在直线上之后所得到的长度。如果某一个向量和非单位向量作点积运算，由于线性变换的特性，可以看成是先在单位向量上进行投影，然后再乘以非单位向量扩大的倍数，也就是该非单位向量的长度

向量也可以理解成某一个线性变换的概念性的缩写记号

Cross products

• 2维讨论

   

  

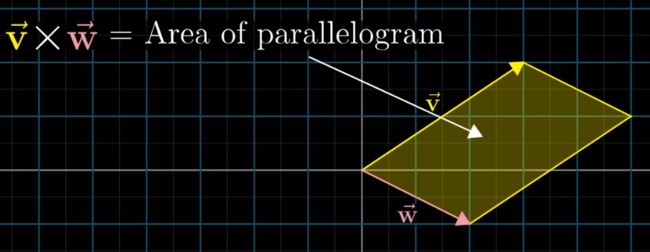
  v和w的叉积，就是它们所围城的这个平行四边形的面积

   

  

  v在w右侧，面积为正

   

  

  v在w左侧，面积为负

   

  

   

  

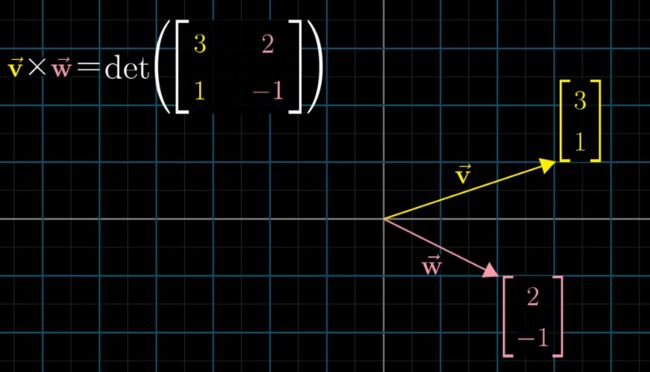
  计算v和w的叉积，只需计算它们所构成的矩阵的determinant。Determinant本身就是度量线性变换前后的比例

   

  

• 基本概念

   

  

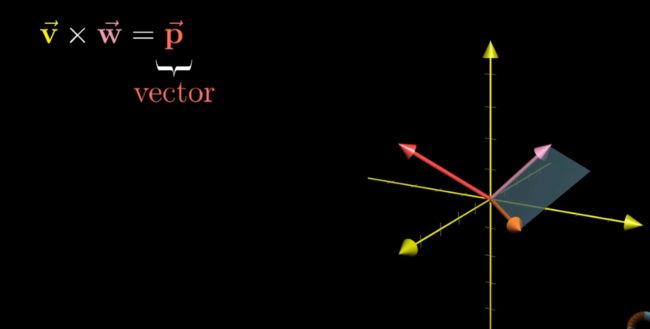
  真正叉积的结果不是一个数值，而是一个向量，两个向量的叉积，生成第三个向量，生成的向量的长度和两个向量所围成的平行四边形的面积相等，而它的方向和平行四边形所在的面相垂直

   

  

  其方向由右手法则所定

• 运算

   

  

   

  

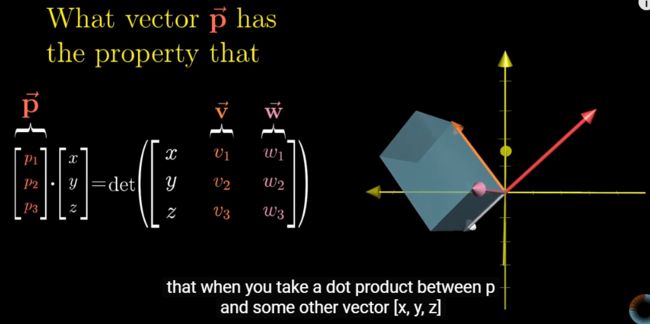
• 运算公式背后的几何意义

   

  

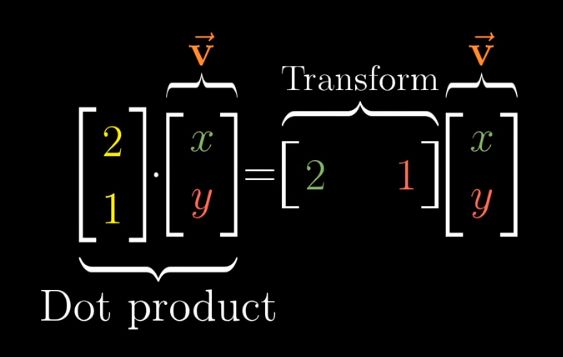
  前一章对偶性中提到的一个向量有其相对应的线性变换矩阵，对任意一个向量x,y作线性变换，其结果和与这个线性变换的矩阵所关联的向量作点积是相同的

   

  

   

  

   

  

  第一步，假设存在这样一个函数，输入任意一个三维向量，输出一个det的值，由v和w及输入的向量u决定。这便是一个从3d到1d的线性变换。其几何意义是该3个向量所围成的平行六面体的体积

   

  

  因为这个变换是线性的，可以用某一个矩阵来描述它

   

  

  由于对偶性，可以将这个矩阵立起来，作为该矩阵对应的向量，并看成其与x,y,z向量的点积

   

  

  左侧点积的结果和P向量的坐标相同

   

  

   

  

  什么样的向量p才能满足，p和x,y,z向量点乘之后的值 = x,y,z向量与v、w向量所围成的平行六面体的体积

   

  

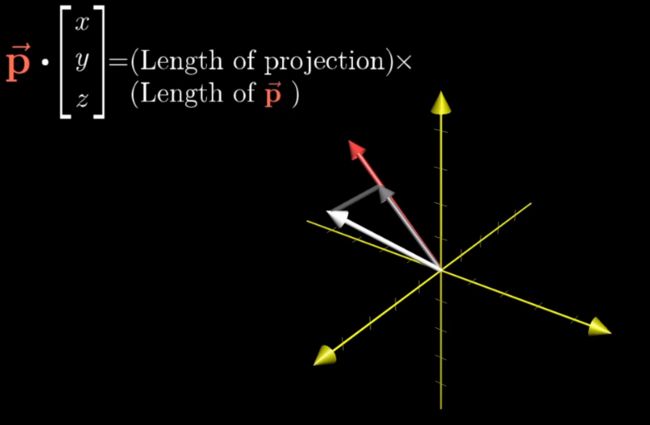
  点乘的几何意义，是投影长度的乘积

   

  

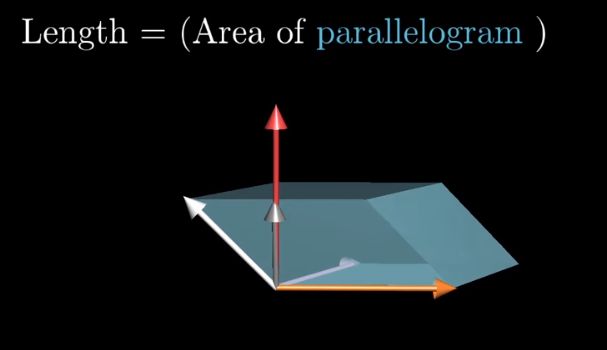
  假如说p没有垂直于v和w所构成的平面，那么p,w,v所构成的平行六面体的体积，是p在垂直于v,w平面上的分量去乘以v和w围成的平行四边形的面积

   

  

  这与用x,y,z向量和垂直于v和w，且长度等于平行四边形面积的向量作点乘的结果是一致的

Change of basis

• 基本定义

   

  

   

  

   

  

  同一个向量，如果选取的basis vectors不同，则其scalars便不同

   

  

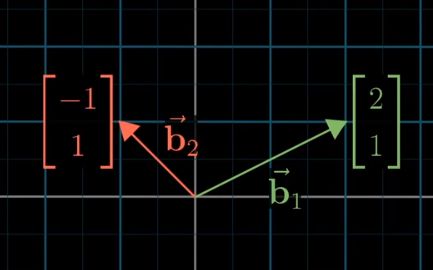
  在正坐标系中，b1和b2被表示成如图

   

  

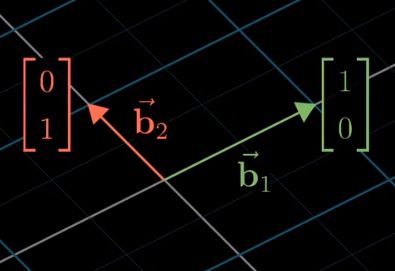
  而从变换basis vectors的角度看，b1和b2还是(1,0)和(0,1)

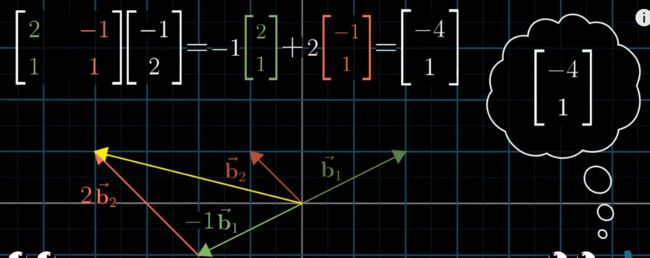
• 运算

   

  

  矩阵的列是在正坐标系下的b1和b2的坐标，（-1，2）是在b1，b2坐标系下的v的坐标，相乘后得到的结果，便是在正坐标系下，v的坐标

   

  

   

  

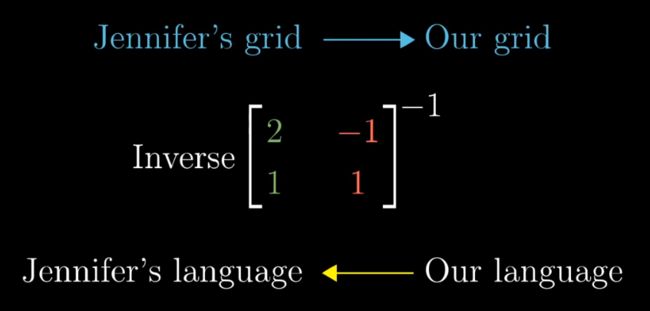
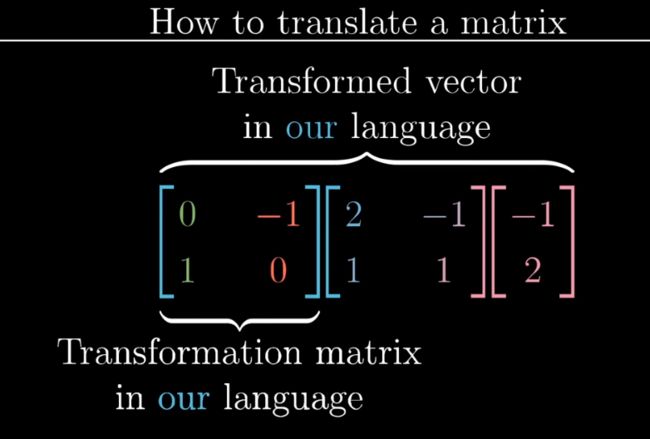
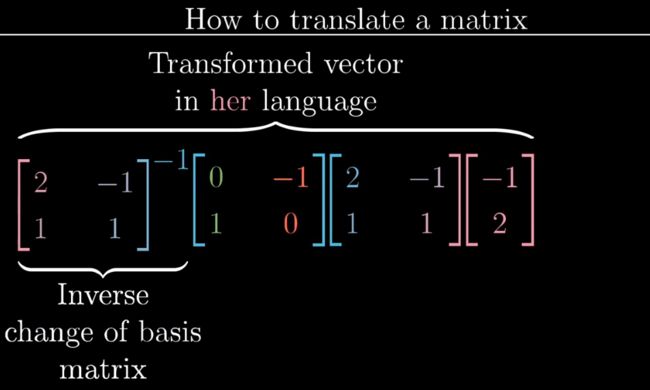
• 把正坐标系下的线性变换翻译成变换基的坐标系下的变换

   

  

  此例中，在我们的正坐标系下是一个旋转90度的变换

   

  

   

  

  三个矩阵乘积的结果便是在Jennifer坐标系下的旋转90度的变换

   

  

   

  

  中间的M是在你坐标系下的变换

Eigenvectors and eigenvalues

• 背景

   

  

  在某一个向量经过某个线性变换之后，它所在的新的位置和原先所在位置经过的直接之间一般都会有所偏离

   

  

  但是有一些向量，在经过线性变换之后，它仍然在经过它原先位置的直线上，线性变换对它的作用仅仅是压缩或者拉伸了

   

  

  对于上例矩阵所描述的线性变换，这些线上的向量还是在原来位置

   

  

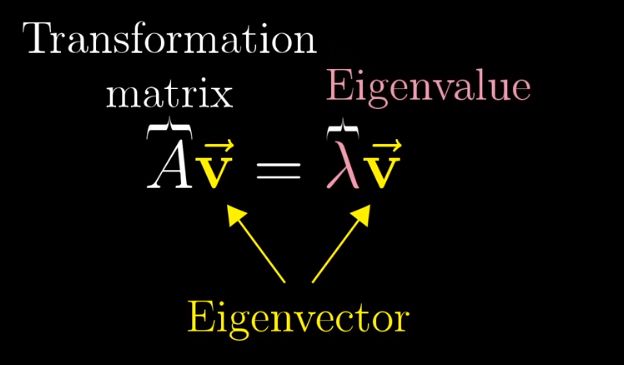
  这些待在原来位置的特殊的向量，就被称为该矩阵的特征向量

   

  

  这些特征向量相对于原来向量的缩放比例，即scalar便是特征值

• 应用

   

  

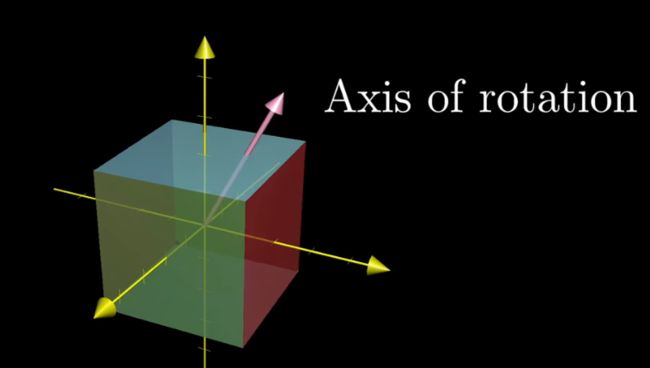
  一个3维的物体，其特征向量是它的旋转轴

   

  

  找到特征向量，便可以减少依赖于自己定义的坐标系，更易于理解线性变换的作用

   

  

   

  

• 计算

   

  

   

  

  如果等式成立，并且有非0的v向量，则一定存在降维，才会把原来不为0的向量，压缩到0向量上来，所以A-λI这个矩阵一定不是满秩的，也就是说其行列式的值为0

• 对角矩阵

   

  

  对角矩阵所有的基向量都是特征向量，对角线上的值便是它的特征值

   

  

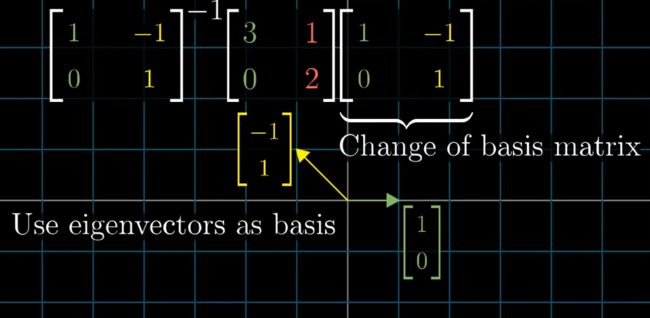
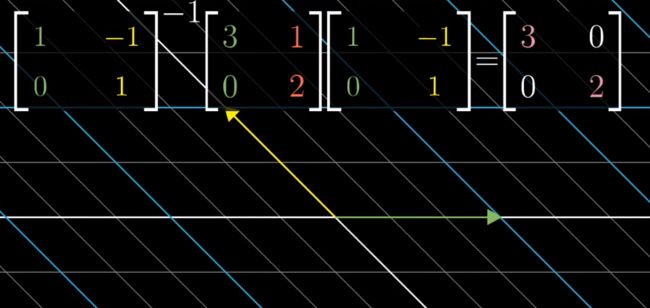
  对于正坐标系下的变换矩阵A，算出它的两个特征向量（1,0）和(-1,1)之后，将这个A变换翻译成以A矩阵的特征向量为基下的变换

新得到的矩阵必然是对角的，并且对角元为对应的特征值，因为以特征向量为基向量的变换中，只有缩放的变换，因此i和j在变换后，只是乘上scalar

Abstract vector spaces

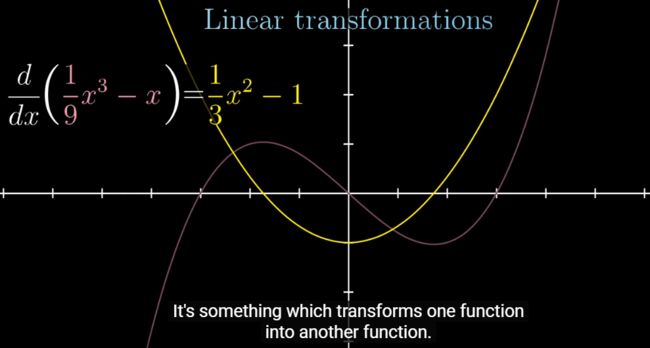
函数其实也具有某种向量的性质

选取basis functions，就类似于选取了basis vector

多项式空间的基有无穷多

98人点赞

数学笔记