2 循环群
循环群是最简单的群了。循环群可以用来研究旋转问题的，比如说等边三角形的旋转。看下面三张图：
分别对应了三种旋转状态不动、旋转一次、旋转两次。既然是研究旋转，我们就可以先试着摸索旋转的规律。比如对于上图的正三角形。我们可以得到以下规律：
旋转一次再旋转一次等于旋转两次；
旋转一次再旋转两次等于没旋转。
这个时候读者就会郁闷了，这就是群论吗？这不小儿科的东西吗？对！这就是小儿科的东西，群论就是从这类小儿科的东西开始的。群论就是把这些小儿科的东西用标准的数学语言去规范，然后从司空见惯的、习以为常的现象中去摸索世界的本质规律。
好了，不吹群论了，我们以符号e、 r r r、 r 2 r^2 r2来表示这三种动作（r是旋转rotate的首字母），这就构成了一个循环群，e就是循环群的单位元，e代表不改变，相当于 r 0 r^0 r0。这个循环群被称为 C 3 C_3 C3。当然循环群不止 C 3 C_3 C3这一种，还有 C 1 C_1 C1、 C 2 C_2 C2、 C 4 C_4 C4、 C 5 C_5 C5一直到 C n C_n Cn。
循环群的乘法，就是“再”的意思，比如旋转两次再旋转两次,用数学语言表示就是 r 2 ⋅ r 2 r^2\cdot r^2 r2⋅r2。旋转两次再旋转两次，加起来旋转了四次，在 C 3 C_3 C3中相当于旋转一次，同理，旋转7次、10次、13次都相当于旋转一次。而4、7、10、13除于3的余数都是1，所以循环群的乘法运算实际上是先加再取余数，专业点的称呼是模加法。所以 r 2 ⋅ r 2 = r r^2\cdot r^2=r r2⋅r2=r是这么算出来的， ( 2 + 2 ) ( m o d 3 ) = 1 (2+2) \ (mod \ 3) =1 (2+2) (mod 3)=1。因为本质是模加法，所以循环群符合交换律，属于阿贝尔群。
知道这个规律后，我们很容易画出 C 3 C_3 C3的乘法表。
⋅ e r r 2 e e r r 2 r r r 2 e r 2 r 2 e r \begin {array}{c|c} \cdot & e & r & r^2 \\ \hline e & e & r & r^2 \\ r & r & r^2 & e\\ r^2 & r^2 & e & r\\ \end {array} ⋅err2eerr2rrr2er2r2er
同样可以很容易画出 C 3 C_3 C3的凯莱图。
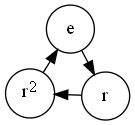
循环群不仅用在平面几何、立体几何里研究旋转，还在量子力学领域用于研究粒子、化学领域用于研究分子。在计算机算法领域，循环队列用到了循环群的计算方法（模加法与模减法）。