标量除、矢量除、正交化

引言

我的都知道标量乘和矢量乘，标量乘就是两个矢量各项元素相乘之和，得到的是一个标量;矢量乘就是两个矢量相乘得到一个新的矢量，该矢量垂直于这两个矢量。对于除法呢，矢量是否有除法呢?是否也是标量除和矢量除呢?

标量除

说到矢量的除法，可能第一反应就是两个向量做比较，可能是模的比值。可以做这个定义，但这个定义用处并不是很大，我有一种用处更大的定义。众所周知，当你用一个尺子测量你的身高，结果是178。常识告诉我们身高是178cm。为什么要写上单位，因为你量取一个东西时，都是用东西的长度除以尺子的单位长度，用下数学式表示：
$$L/i=178$$
式中：$L$是身高，$i$是尺子的单位，常用cm。
如果用两把尺子垂直摆放，则不仅来测量你的身高，还能测量胖瘦。这样可以用两个式子表示
$$\{\begin{array}{lc}L/i=178& \\ W/j=34& \end{array}$$
式中$i$和$j$组成一组矢量基$M$，$L$和$W$是被衡量的对象矢量$P$分解到$i$方向和$j$方向的两个矢量，数学可以这样描述:
$$P/M=(\begin{array}{lc}P/i& P/j\end{array})=(\begin{array}{lc}L/i& W/j\end{array})=(\begin{array}{lc}|L|/|i|& |W|/|j|\end{array})=(\begin{array}{lc}178& 34\end{array})$$这里的$P/i$，$P/j$，$L/i$，$W/j$就是矢量之间的除法。$P/M$是矢量与矢量基的除法，由于矢量基有多个矢量，矢量对矢量基的除法是矢量对基内的每个矢量进行除法。我们定义一个矢量A对另一个矢量B的标量除为该矢量A在矢量B中的投影长度除以矢量B的长度。上式中$L$就是$P$在$i$中的投影，$W$就是$P$在$j$中的投影，所以
$$P/i=L/i，P/j=W/j$$对于两个相互平行的矢量，将两个矢量的模相除才有意义，两个相互平行的矢量的标量除就是两个矢量的模相除。所以$$L/i=178,W/j=34$$标量除法的数学定义如下。$$a/b=pro{j}_{b}a/b=\frac{|pro{j}_{b}a|}{|b|}$$几何表示如下
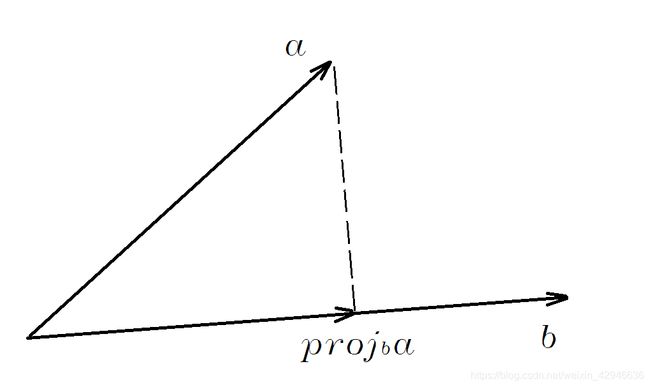根据上述的定义可以进一步拓展，
$$a/b=\frac{|a|cos<a,b>}{|b|}=\frac{|a|}{|b|}\frac{|ab|}{|b|}=\frac{ab}{|b{|}^2}$$
若$a=(a_x,a_y,a_z)$,$b=(b_x,b_y,b_z)$则
$$a/b=\frac{a_x{b}_x+a_y{b}_y+a_z{b}_z}{b_x^2+b_y^2+b_z^2}$$标量除有线性的关系，若$a=a_1+a_2$，那么$$a/b=a_1/b+a_2/b$$
如果$a$与$b$垂直，那么$a/b=0$
可以简单证明得到

矢量除

有标量除，是否也有矢量除。不管有没有这个自然概念，但可以创造啊。数学早已经走出了从0,1,2,3…和长宽高等自然概念中提取素材的时代，走向了从数学本身来提取素材或者创造概念的时代。
矢量乘有两个特点：1、垂直于参与乘法的矢量，2、模与正弦有关。类比这个，可以按下图定义矢量除

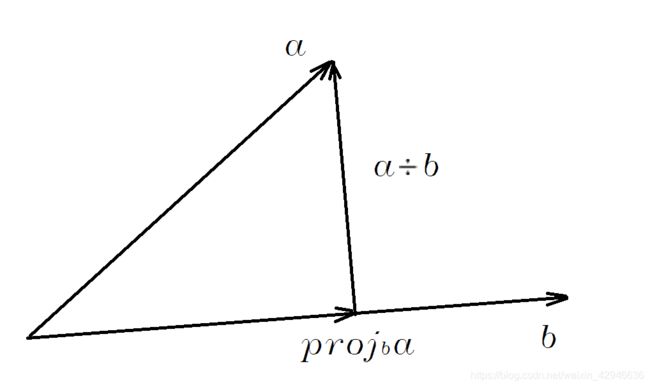
图中$a÷b$就是$a$对$b$的矢量除，它部分满足两个特点，与$b$垂直，与$a$模存在正弦的关系。矢量除可以这么定义：矢量$a$对矢量$b$的矢量除就是矢量$a$对垂直于矢量$b$且与矢量$a$和矢量$b$共面的矢量的投影。根据定义
$$a÷b=a-a/b\cdot b$$
若$a=(a_x,a_y,a_z)$,$b=(b_x,b_y,b_z)$则
$$\begin{gathered} a÷b=\left(\begin{array}{c}{a}_x-\frac{a_x{b}_x+a_y{b}_y+a_z{b}_z}{b_x^2+b_y^2+b_z^2}{b}_x\\ a_y-\frac{a_x{b}_x+a_y{b}_y+a_z{b}_z}{b_x^2+b_y^2+b_z^2}{b}_y\\ a_y-\frac{a_x{b}_x+a_y{b}_y+a_z{b}_z}{b_x^2+b_y^2+b_z^2}{b}_y\end{array}\right) \\ =\left(\begin{array}{c}{a}_x{b}_y^2+a_x{b}_z^2-a_y{b}_y{b}_x-a_z{b}_z{b}_x\\ a_y{b}_x^2+a_y{b}_z^2-a_x{b}_x{b}_y-a_z{b}_z{b}_y\\ a_z{b}_x^2+a_z{b}_y^2-a_x{b}_x{b}_z-a_y{b}_y{b}_z\end{array}\right)/(b_x^2+b_y^2+b_z^2) \\ =\left(\begin{array}{c}{b}_y\left|\begin{array}{cc}{a}_x& a_y\\ b_x& b_y\end{array}\right|-b_z\left|\begin{array}{cc}{a}_z& a_x\\ b_x& b_y\end{array}\right|\\ b_z\left|\begin{array}{cc}{a}_y& a_z\\ b_y& b_z\end{array}\right|-b_x\left|\begin{array}{cc}{a}_x& a_y\\ b_x& b_y\end{array}\right|\\ b_x\left|\begin{array}{cc}{a}_z& a_x\\ b_z& b_x\end{array}\right|-b_y\left|\begin{array}{cc}{a}_y& a_z\\ b_y& b_z\end{array}\right|\end{array}\right)/(b_x^2+b_y^2+b_z^2) \\ =b\times a\times b/|b{|}^2 \end{gathered}$$即$a÷b=b\times a\times b/|b{|}^2$
矢量除有线性的关系，若$a=a_1+a_2$，那么$$a÷b=a_1÷b+a_2÷b$$
如果$a$与$b$垂直，那么$$\begin{gathered} a÷b=a \\ c÷a÷b=c÷b÷a=c-c/a\cdot a-c/b\cdot b \end{gathered}$$
矢量除与标量除的混合运算
$$(a÷b)/c=a/c-a/b\cdot b/c$$
还有很多混合运算，后续我将一个一个推导
$$\begin{gathered} a/(b÷c)=? \\ a\cdot (b÷c)=? \end{gathered}$$

投影

矢量$a$向矢量$b$投影我们记为$pro{j}_{b}a$，在平面内，矢量$a$向垂直于矢量$b$矢量投影我们记为$pre{p}_{b}a$，也可以称其为垂矢。他们与标量除和矢量除有如下关系
$$\begin{gathered} pro{j}_{b}a=a/b\cdot b \\ pre{p}_{b}a=a÷b \end{gathered}$$矢量向平面的投影又如何，矢量向平面的垂矢又如何呢？已知某平面内两个向量$a$和$b$，平面外的一个矢量$c$，如图所示

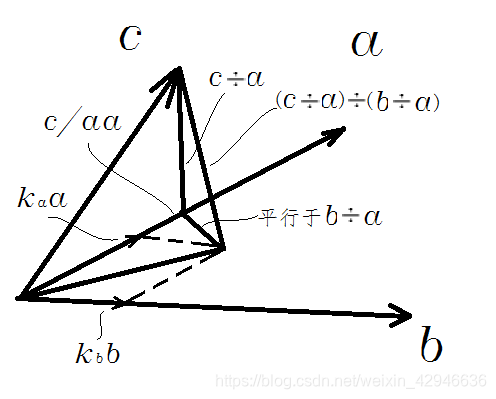
可以肯定c在平面的投影$pro{p}_{ab}c=k_a\cdot a+k_b\cdot b$，当然还有很多种表达都可以，这种在几何上体现形式更好，符合矢量合成的平行四边形的美感。可知
$$\begin{gathered} pro{j}_{ab}c/a=c/a \\ pro{j}_{ab}c/b=c/b \end{gathered}$$
所以
$$\begin{gathered} (k_a\cdot a+k_b\cdot b)/a=k_a+k_b\cdot b/a \\ (k_a\cdot b+k_b\cdot b)/b=k_a\cdot a/b+k_b \end{gathered}$$

求解$k_a$和$k_b$
$$\begin{gathered} k_a=\frac{c/b\cdot b/a-c/a}{b/a\cdot a/b-1}=\frac{(c÷b)/a}{1-b/a\cdot a/b} \\ {k}_b=\frac{c/a\cdot a/b-c/b}{b/a\cdot a/b-1}=\frac{(c÷a)/b}{1-b/a\cdot a/b} \end{gathered}$$
当$a$和$b$垂直时$a/b=0,b/a=0$，所以
$$\begin{gathered} k_a=c/a \\ {k}_b=c/b \end{gathered}$$
垂矢的求法为$c$先对$a$求垂矢得$c÷a$，再对$a$在平面上垂直矢量$b÷a$求垂矢，即$(c÷a)÷(b÷a)$，可以证明此矢量垂直于$a$和$b÷a$，所以此矢量垂直于平面，所以
$$pre{p}_{ab}c=(c÷a)÷(b÷a)$$
也可以表达为
$$pre{p}_{ab}c=(c÷b)÷(a÷b)$$
因此$c$在平面上投影的另一种表达为
$$pro{p}_{ab}c=c-(c÷a)÷(b÷a)$$
存在如下两个关系$$(c÷a)÷(b÷a)+\frac{(c÷b)/a}{1-b/a\cdot a/b}\cdot a+\frac{(c÷a)/b}{1-b/a\cdot a/b}\cdot b=c$$
$$(c÷a)÷(b÷a)//a\times b$$
后续证明

正交化

正交化是指已知一系列的不平行矢量$a_1,a_2,a_3,a_4...a_n$求其所在空间的正交基$b_1,b_2,b_3,b_4...b_n$。有了这些正交的基，继续单位化，就构建了一套坐标系。之前投影讲到矢量$a$到$b$的垂矢，矢量$c$到矢量$a$和$b$组建的平面的垂矢就是一个正交化的过程。用$a_1$代替$a$，$a_2$代替$b$，$a_3$代替$c$，$b_1,b_2,b_3$为生成的正交矩阵，其过程如下
$$\begin{gathered} b_1=a_1 \\ {b}_2=a_2÷b_1 \\ {b}_3=(a_3÷b_1)÷b_2 \end{gathered}$$
扩展到四维呢?扩展到多维呢?大胆假设
$$\begin{gathered} b_1=a_1 \\ {b}_2=a_2÷b_1 \\ {b}_3=a_3÷b_1÷b_2 \\ {b}_4=a_4÷b_1÷b_2÷b_3 \\ ⋮ \\ {b}_n=a_n÷b_1÷b_2÷b_3÷\cdots ÷b_{n-1} \end{gathered}$$
小心求证: 求证的目标就是$b_1,b_2,b_3,\cdots ,b_{n-1},b_n$相互两两垂直，采用递推法进行证明:
$n=2$时，因为$b_2=a_2÷b_1$根据矢量除的定义就可知$b_2$与$b_1$垂直
$n=3$时，$$\begin{gathered} b_3=a_3÷b_1÷b_2 \\ {b}_3=(a_3-a_3/b_1\cdot b_1)÷b_2 \\ {b}_3=a_3÷b_2-a_3/b_1\cdot b_1÷b_2 \end{gathered}$$
因为$b_1$与$b_2$垂直，所以$b_1÷b_2=b_1$，所以$b_3=a_3-a_3/b_2\cdot b_2-a_3/b_1\cdot b_1$
所以
$$\begin{gathered} b_3/b_1=(a_3-a_3/b_2\cdot b_2-a_3/b_1\cdot b_1) \\ {b}_3/b_1=a_3/b_1-a_3/b_2\cdot b_2/b_1-a_3/b_1\cdot b_1/b_1 \end{gathered}$$
因为$b_2$与$b_1$垂直，所以$b_2/b_1=0$，所以
$$\begin{gathered} b_3/b_1=a_3/b_1-a_3/b_1\cdot b_1/b_1 \\ {b}_3/b_1=a_3/b_1-a_3/b_1=0 \end{gathered}$$
所以$b_3$与$b_1$垂直，$b_3$与$b_2$的垂直关系可采用同样的方式证明，当然如果熟悉矢量除的定义，也可以直接看出$b_3$与$b_2$的关系。
若$n=k-1$时$b_1,b_2,b_3,\cdots ,b_{k-1}$相互两两垂直，那么$n=k$时
$$\begin{gathered} b_k=a_k÷b_1÷b_2÷b_3÷\cdots ÷b_{k-1} \\ {b}_k=a_k-a_k/b_1\cdot b_1-a_k/b_2\cdot b_2-a_k/b_3\cdot b_3-\cdots -a_k/b_{n-1}\cdot b_{n-1} \end{gathered}$$
从$b_1,b_2,b_3,\cdots ,b_{k-1}$任意选择一个$k_i$，计算$b_k/b_i$
$$\begin{gathered} b_k/b_i=a_k/b_i-a_k/b_1\cdot b_1/b_i-a_k/b_2\cdot b_2/b_i-a_k/b_3\cdot b_3/b_i-\cdots \\ -a_k/b_i\cdot b_i/b_i-\cdots -a_k/b_{n-1}\cdot b_{n-1}/b_i \end{gathered}$$所以$b_k/b_i=a_k/b_i-a_k/b_i\cdot b_i/b_i=0$
所以$b_k$与$b_1,b_2,b_3,\cdots ,b_{k-1}$任意一个矢量垂直，也就是$b_1,b_2,b_3,\cdots ,b_k$内的所以矢量都相互两两垂直。证明完毕!
等等，或许有人疑问，为啥$$b_k=a_k-a_k/b_1\cdot b_1-a_k/b_2\cdot b_2-a_k/b_3\cdot b_3-\cdots -a_k/b_{n-1}\cdot b_{n-1}$$这个可以自行递推证明一下。
提示一下，对于$b_1,b_2,b_3,\cdots ,b_m$内的所有矢量相互两两垂直，若下式成立$$a÷b_1÷b_2÷\cdots ÷b_{m-1}=a-a/b_1\cdot b_1-a/b_2\cdot b_2-\cdots -a/b_{m-1}\cdot b_{m-1}$$则$$a÷b_1÷b_2÷\cdots ÷b_m=a-a/b_1\cdot b_1-a/b_2\cdot b_2-\cdots -a/b_{m-1}\cdot b_{m-1}-a/b_m\cdot b_m$$

施密特正交化与QR分解

根据上节内容，我们知道
$$\begin{gathered} b_1=a_1 \\ {b}_2=a_2÷b_1 \\ {b}_3=a_3÷b_1÷b_2 \\ {b}_4=a_4÷b_1÷b_2÷b_3 \\ ⋮ \\ {b}_n=a_n÷b_1÷b_2÷b_3÷\cdots ÷b_{n-1} \end{gathered}$$和$$b_k=a_k-a_k/b_1\cdot b_1-a_k/b_2\cdot b_2-a_k/b_3\cdot b_3-\cdots -a_k/b_{n-1}\cdot b_{n-1}$$
那么可以将$b_1,b_2,b_3\cdots b_n$展开来，
$$\begin{gathered} b_1=a_1 \\ {b}_2=a_2-a_2/b_1\cdot b_1 \\ {b}_3=a_3-a_3/b_1\cdot b_1-a_3/b_2\cdot b_2 \\ {b}_4=a_4-a_4/b_1\cdot b_1-a_4/b_2\cdot b_2-a_4/b_3\cdot b_3 \\ ⋮ \\ {b}_n=a_n-a_n/b_1\cdot b_1-a_n/b_2\cdot b_2-a_n/b_3\cdot b_3-\cdots -a_n/b_{n-1}\cdot b_{n-1} \end{gathered}$$
所以
$$\begin{gathered} b_1=a_1 \\ {b}_2=a_2-k_{2,1}\cdot b_1 \\ {b}_3=a_3-k_{3,1}\cdot b_1-k_{3,2}\cdot b_2 \\ {b}_4=a_4-k_{4,1}\cdot b_1-k_{4,2}\cdot b_2-k_{4,3}\cdot b_3 \\ ⋮ \\ {b}_n=a_n-k_{n,1}\cdot b_1-k_{n,2}\cdot b_2-k_{n,3}\cdot b_3-\cdots -k_{n,n-1}\cdot b_{n-1} \end{gathered}$$其中
$$k_{i,j}=\{\begin{array}{ll}{a}_i/b_j=\frac{a_i\cdot b_j}{|a_i{|}^2};& (i>j)\\ 1,& (i=j)\end{array}$$这就是施密特正交化，将所有$a$放在等号左边，所有$b$放在等号右边
$$\begin{gathered} a_1=b_1 \\ {a}_2=k_{2,1}\cdot b_1+b_2 \\ {a}_3=k_{3,1}\cdot b_1+k_{3,2}\cdot b_2+b_3 \\ {a}_4=k_{4,1}\cdot b_1+k_{4,2}\cdot b_2+k_{4,3}\cdot b_3+b_4 \\ ⋮ \\ {a}_n=k_{n,1}\cdot b_1+k_{n,2}\cdot b_2+k_{n,3}\cdot b_3+\cdots +k_{n,n-1}\cdot b_{n-1}+b_n \end{gathered}$$将所有$b$换成其单位向量$q$，则有
$$\begin{gathered} a_1=|b_1|\cdot q_1 \\ {a}_2=k_{2,1}|b_1|\cdot q_1+|b_2|\cdot q_2 \\ {a}_3=k_{3,1}|b_1|\cdot q_1+k_{3,2}|b_2|\cdot q_2+|b_3|\cdot q_3 \\ {a}_4=k_{4,1}|b_1|\cdot q_1+k_{4,2}|b_2|\cdot q_2+k_{4,3}|b_3|\cdot q_3+|b_4|\cdot q_4 \\ ⋮ \\ {a}_n=k_{n,1}|b_1|\cdot q_1+k_{n,2}|b_2|\cdot q_2+k_{n,3}|b_3|\cdot q_3+\cdots +k_{n,n-1}|b_{n_1}|\cdot q_{n-1}+|b_n|\cdot q_n \end{gathered}$$
若写成矩阵的形式就是
$$\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\\ \cdots \\ a_n\end{array}\right)=\left(\begin{array}{ccccc}{r}_{1,1}& 0& 0& \cdots & 0\\ r_{2,1}& r_{2,2}& 0& \cdots & 0\\ r_{3,1}& r_{3,2}& r_{3,3}& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ r_{n,1}& r_{n,2}& r_{n,3}& \cdots & r_{n,n}\end{array}\right)\left(\begin{array}{c}{q}_1\\ q_2\\ q_3\\ \cdots \\ q_n\end{array}\right)$$
其中$r_{i,j}=k_{i,j}|b_j|$
这就是QR分解，$Q$是一个单位正交矩阵，放在复域，称为酉矩阵
$$Q=\left(\begin{array}{c}{q}_1\\ q_2\\ q_3\\ \cdots \\ q_n\end{array}\right)$$
经过QR分解，一个满秩矩阵可以分解成一个下三角矩阵乘单位正交矩阵，这可以用于线性最小二乘问题的求解和矩阵特征值的计算。