【JLOI】02金猪贺岁-贪心策略

【JLOI】02金猪贺岁-贪心策略
贪心策略！
NOIP普及组重点题型
然后，别以为算法很基础，IOI都在考贪心策略！
你问我贪心策略是啥？那就是：局部最优解就是最优解
【引入例题】P1031 均分纸牌
思考：
【算法1】如果你是大神，你可以发现N很小，然后你就可以N^3地dp
【算法2】考虑贪心。我们可以用转化法，令opt为原数组的平均数，让每个数字-=opt，然后当a[i]（第i堆纸牌与平均数的关系）不等于0时，a[i+1]=a[i+1]+q[i],移动次数加1。
【算法3】由于只能移动相邻的，就可以大暴力
算法2与算法3的时间复杂度均为O(n)
算法2代码：

#include
using namespace std;
int n,a[1001],ave=0,i,j;
int main()
{
    cin >> n;
    int step=0;
    for(i=1;i<=n;i++)
    {
        cin >> a[i];
        ave+=a[i];
    }
    ave/=n;//计算平均数
    for(i=1;i<=n;i++) a[i]-=ave;//减去平均数
    i=1; j=n;
    while(a[i]==0&&i<n) i++;//排除万难（从头开始符合条件的不算）   
    while(a[j]==0&&j>1) j--;//排开万险（从尾开始符合条件的不算）   
    while(i<j)//开始贪心
    {
        a[i+1]+=a[i];
        a[i]=0;
        step++;//推拿过程
        i++;
        while(a[i]==0&&i<j) i++;//再次排除万难
    }
    cout << step << endl;//得出答案
    return 0;
}

贪心的美妙之处就在于：一题一贪，策略永不同。事实上考试时不用证明贪心的正确性，只要找到规律即可。但是还是应该了解贪心的证明
对于这一道题：由于只能交换相邻的，所以如果a[i]不符合条件就推拿到a[i+1]，这样的策略显然是正确的
【引入例题】P1803 凌乱的yyy / 线段覆盖
著名又经典的贪心问题
即最大不重线段覆盖问题
思考这类问题，可以画图

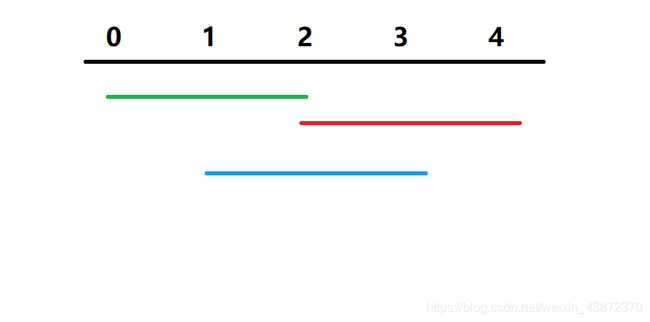
答案当然选绿色&红色线段
我们开始思考贪心策略：
按长度从小到大排？
十分容易举出反例：

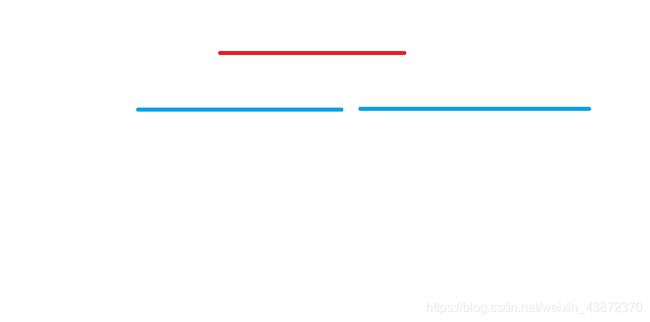
按照我们的贪心策略，应该选红色线段。事实上两条蓝色线段选了更好！

KO!

第二个贪心策略：
右端点为第一关键字从小到大排
貌似是对的
代码：

#include
using namespace std;
struct node
{
 int l,r;
}; 
const int N=100005;
const int M=1000005;
int n;
node a[M];
int f[N];
int l=0,ans=0;
bool cmp(node x,node y)
{
 if(x.r==y.r) return x.l<y.l;
 else return x.r<y.r;
}
int main()
{
 scanf("%d",&n);
 for(int i=1;i<=n;i++)
  scanf("%d%d",&a[i].l,&a[i].r);
 sort(a+1,a+n+1,cmp);
 l=1;
 ans=1;
 for(int i=1;i<=n;i++)
 {
  if(a[i].l>=a[l].r)
  {
   ans++;
   l=i;
  }
 }
 cout << ans << endl;
 return 0;
} 

【难·贪心】

P2114 [NOI2014]起床困难综合症
这道题要利用位运算的性质以及二进制的好处
你就算是11111111111111111也比不过100000000000000000
位数大的必胜
所以可以从高到低贪心
十分easy

#include
using namespace std;
int n,m;
char s[10001];
int x=0,y=-1,t;
int ans=0;
int main()
{
 scanf("%d%d",&n,&m);
 for(int i=1;i<=n;i++)
 {
  scanf("%s%d",s,&t);
  if(s[0]=='A') x&=t,y&=t;
  if(s[0]=='O') x|=t,y|=t;
  if(s[0]=='X') x^=t,y^=t;
 }
 for(int i=29;i>=0;i--)
 {
  if(x>>i&1) ans+=1<<i;//x>>j:x的第j位 
  else if(y>>i&1&&(1<<i)<=m)
  {
   ans+=1<<i;
   m-=1<<i;
  }
 }
 printf("%d\n",ans);
    return 0;
}

P2672 [NOIP普及组2015] 推销员
从样例容易看出用贪心做，即第一次选了curr，则第二次在第一次的基础上再选出下一个。即要么选择curr左边的a，要么选择curr右边的b，若选择左边的a，则总疲劳值ans会加上A[a],若选择右边的b，则总疲劳值ans需加上A[b]+2*(S[b]-S[curr])。

总之， 下一次选择必基于上一次的选择 。

但问题来了，

怎么证明这个想法是对的？！

证明：
若已知Xn为拜访n户时的最优解，Xn={A[k1]+A[k2]+…+A[kn]}+2S[kn],即从近到远选择了{k1,k2,…kn}。
假设Yn+1为拜访n+1户时的最优解，Yn+1={A[p1]+A[p2]+…+A[pn]+A[pn+1]+2S[pn+1],且{p1,p2,…,pn+1}不包含{k1,k2,…kn}。
分类讨论 如下：
1）当pn+1==kn,即同户时，Yn+1 = {A[p1]+A[p2]+…+A[pn]+A[pn+1]}+2S[kn] < Xn+A[pk],其中pk不属于{k1,k2,…kn}
2）当S[pn+1]S[kn] < Xn+A[pk],其中pk不属于{k1,k2,…kn}
3） 当S[pn+1]>S[kn],即pn+1在kn的右边时，Yn+1 = {A[p1]+A[p2]+…+A[pn]+A[pn+1]}+2*S[kn]+2(S[pn+1]-S[kn]) < Xn + A[pn+1] +2(S[pn+1]-S[kn])
综上，若{p1,p2,…,pn+1}不包含{k1,k2,…kn}，Yn+1必不是最优解。
那么若{p1,p2,…,pn+1}包含{k1,k2,…kn}，易知，Xn+1=Xn+max{左,右}。
那么若左边的最大值和右边的最大值相等时该取谁呢？
其实取取谁都一样，比如Xn最优解的最右方为第k户，左边最大为第k1户，右边最大为第k2户，
那么不管取左还是取右,得到的Xn+1值都一样，那么对于这两种取法会不会影响到Xn+2呢？
其实如果先取左k1，必然在Xn+2取到k2;如果先取右k2,必然在Xn+2取到k1,因为先取k2的话，右边的老二的值必然减小，肯定不如k1的大。
代码：

#include
using namespace std;
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define frep(i,a,b) for(int i=a;i>=b;i--)
#define WOSHIDAJURUO scanf("%d",&n);rep(i,1,n) scanf("%lld",&q[i].dis);rep(i,1,n) scanf("%lld",&q[i].tir);sort(q+1,q+n+1,cmp);first_choose=1;fistance=q[1].dis*2;rep(i,2,n){ if(q[i].tir+q[i].dis*2>fistance+q[first_choose].tir){  fistance=q[i].dis*2;  first_choose=i; } }  printf("%lld\n",fistance+q[first_choose].tir);ans=fistance+q[first_choose].tir;rep(i,1,n){ if(i==first_choose) continue; ans+=q[i].tir; if(q[i].dis*2>fistance){  ans=ans-fistance+q[i].dis*2;  }  printf("%lld\n",ans); }  return 0;
#define _ZTYAKIOI_ scanf("%d",&n);rep(i,1,n) scanf("%lld",&q[i].dis);rep(i,1,n) scanf("%lld",&q[i].tir);sort(q+1,q+n+1,cmp);first_choose=1;fistance=q[1].dis*2;rep(i,2,n){ if(q[i].tir+q[i].dis*2>fistance+q[first_choose].tir){  fistance=q[i].dis*2;  first_choose=i; } }  printf("%lld\n",fistance+q[first_choose].tir);ans=fistance+q[first_choose].tir;rep(i,1,n){ if(i==first_choose) continue; ans+=q[i].tir; if(q[i].dis*2>fistance){  ans=ans-fistance+q[i].dis*2;  }  printf("%lld\n",ans); }  return 0;
typedef long long ll;
const int N=100005;
struct node{
 ll dis;
 ll tir;
};
node q[N];
int n; 
ll ans=0;
int first_choose;//第一次选的
ll fistance;//第一次的路径 
bool cmp(node x,node y){
 return x.tir>y.tir;
}
int main(){
 //
 //WOSHIDAJURUO
 _ZTYAKIOI_ 
 //
} 

and?

贪心和其它算法的结合/贪心的其它的奇奇怪怪的用处

【二分答案+贪心】

举个例子：P1316 丢瓶盖
二分答案，用贪心check
代码：

#include
using namespace std;
int a[1000005],n,B;
int one()
{
    int l=1;
    int r=a[n]-a[1];
    int mid;
    int tot,i,j;
    while(l+1<r)
    {
        tot=0;
        mid=(l+r)/2;
        int x=0;
        i=1;
        while(i<=n)
        {
            x=i+1;
            while(a[x]-a[i]<mid&&x<=n)
                x++;
            tot+=x-i-1;
            i=x;
        }
        if(tot<=B) l=mid;
        else r=mid;
    }
    return l;
}
int main()
{
    scanf("%d%d",&n,&B);
    B=n-B;
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    sort(a+1,a+n+1);
    printf("%d\n",one());
    return 0;
}

贪心+高精度

题目挺多的
就拿T63582（高精度）末日的时候有没有空？来说

题目背景

章原深爱着禾填田
但是好景不长，邪恶的轻阉鸡来了，他要统治世界
生命的最后一秒，他俩依然手牵手面对死亡······
然后悲剧发生了。

题目描述

章原把禾填田的手指掰了下来！
也不知道掰了几根。
话说禾填田几根手指也不知道
不过也好，这样就可以拯救世界了！
然后他们就用手指拯救了世界！
不过他们想知道，这几根手指最多能发挥的力量。
力量=所有根数的乘积
当然你已经知道了手指长度之和

输入输出格式

输入格式：

第一行一个整数n表示手指长度和

输出格式：

答案

输入输出样例

输入样例#1：

1

输出样例#1：

1

输入样例#2：

6

输出样例#2：

9

输入样例#3：

10

输出样例#3：

36

输入样例#4：

247

输出样例#4：

1773705952972151079792998522476599571212

说明

50%n小于等于100
n小于等于10000
首先这道题的贪心实在是太简单了！
小学奥数级别
能拆3就拆3
剩下的拆2
但系，要用高精度
哈哈哈哈哈哈哈哈
代码：

#include
using namespace std;
int n;
int t;
int a[1000001],len;
int weizhi(int x)
{
 int kum=0;
 while(x>0)
 {
  kum++;
  x/=10;
 }
 return kum;
}
int pluss(int x)
{
 for(int i=1;i<=len;i++)
 {
  a[i]=a[i]*x;
 }
 for(int i=1;i<=len;i++)
 {
  a[i+1]+=a[i]/100000000;
  a[i]%=100000000; 
 }
 while(a[len+1]>0)
 {
  len++;
  a[len+1]+=a[len]/100000000;
  a[len]%=100000000;
 }
}
int main()
{
  scanf("%d",&n);
  memset(a,0,sizeof(a));
  len=1,a[1]=1;
  if(n%3==0)
  {
   for(int i=1;i<=n/3;i++)
   {
    pluss(3);
   }
  } 
  else if(n%3==1)
  {
   for(int i=1;i<=n/3-1;i++)
    pluss(3);
   pluss(2);
   pluss(2);
  }
  else if(n%3==2)
  {
   for(int i=1;i<=n/3;i++)
   {
    pluss(3);
   }
   pluss(2);
  }
  for(int i=len;i>=1;i--)
  {
   if(i!=len)
   {
    int sum=weizhi(a[i]);
    for(int kkk=1;kkk<=8-sum;kkk++)
     printf("0");
   } 
   printf("%d",a[i]);
  }
  printf("\n");
 return 0;
} 

dijkstra

dijkstra是一种用贪心来求单源最短路的算法
它的贪心方法是：选最近的标记，拿被标记的更新没被标记的
显然，如果绕路比直走长，肯定选直走
参考代码：（普通dijkstra O(n^2) ）

#include
using namespace std;
//538976288
int n,m,used[500001],dis[500001],s;
int head[500001],value[500001],edd[500001],nxt[500001],cnt=0;
void addege(int a,int b,int c)
{
    cnt++;
    edd[cnt]=b,value[cnt]=c;
    nxt[cnt]=head[a];
    head[a]=cnt;
}
int main()
{
    scanf("%d%d%d",&n,&m,&s); 
    memset(dis,-1,sizeof(dis));
    memset(used,0,sizeof(used));
    for(int j=1;j<=m;j++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        addege(a,b,c);
    } 
    dis[s]=0;
    for(int _i=1;_i<=n;_i++)
    {
        int u=0,num=-1;
        for(int i=1;i<=n;i++)
        {
            if(dis[i]!=-1&&used[i]==0&&(num==-1||num>dis[i]))
            {
                num=dis[i];
                u=i;
            }
        }
        used[u]=1;
        for(int s=head[u];s!=0;s=nxt[s])
        {
            int v=edd[s];
            if(used[v]==0&&value[s]!=-1&&(dis[v]>dis[u]+value[s]||dis[v]==-1))
            {
                dis[v]=dis[u]+value[s];
            }
        }
    }
    for(int i=1;i<n;i++)
    {
        if(dis[i]==-1) dis[i]=2147483647;
        cout << dis[i] << " ";
    } 
    cout << dis[n] << endl;      
    return 0;
}

（堆优化的dijkstra O((n+m)logn) ）

#include
using namespace std;
int n,m,s,cnt=0;
long long dis[500001];
bool used[500001];
vector<int> f[500001];
long long hed[500001],tal[500001],val[500001],nxt[500001];
struct aa
{
    int v,pos;
} ;
bool operator<(const aa &a,const aa &b) //重载小于运算符
{
    return a.v>b.v;
}
priority_queue<aa> q;//堆优化 
void addege(int x,int y,int z)
{
 cnt++;
 tal[cnt]=y;
 val[cnt]=z;
 nxt[cnt]=hed[x];
 hed[x]=cnt;
}
void push(int v,int pos)
{
    aa a;
    a.pos=pos,a.v=v;
    q.push(a);
}
int main()
{
 memset(used,0,sizeof(used));
 memset(dis,-1,sizeof(dis));
 scanf("%d%d%d",&n,&m,&s);
 for(int i=1;i<=m;i++)
 {
  int x,y,z;
  scanf("%d%d%d",&x,&y,&z);
  if(x==y) continue;
  addege(x,y,z);
 }
 for(int i=1;i<=n;i++)
 {
  dis[i]=2147483647;
  used[i]=0;
 }
 dis[s]=0;
 push(0,s);
 while(!q.empty())
 {
  aa u=q.top();
  q.pop();
  if(used[u.pos]==1) continue;
  used[u.pos]=1;
  for(int i=hed[u.pos];i;i=nxt[i])
  {
   int v=tal[i];
   if(used[v]==0&&dis[v]>u.v+val[i])
   {
    dis[v]=dis[u.pos]+val[i];
    push(dis[v],v);
   }
  }
 }
 for(int i=1;i<n;i++)
 {
  if(dis[i]==2147483647) dis[i]=-1;
  printf("%d ",dis[i]);
 }
 if(dis[n]==2147483647) dis[n]=-1;
 printf("%d\n",dis[n]);
 return 0;
} 

prim

最小生成树prim算法
思路和dijkstra一毛一样
就不再放代码了

高级贪心

可以和图论、单调栈、单调队列等高级算法结合，会很难

THE END