【详解+推导！！】Policy Gradient 策略梯度法

Policy Gradient，策略梯度法是强化学习中的一种常用方法。
比较详细的推导可以看：https://datawhalechina.github.io/easy-rl/#/chapter4/chapter4?id=tips

1. 定义强化学习的问题

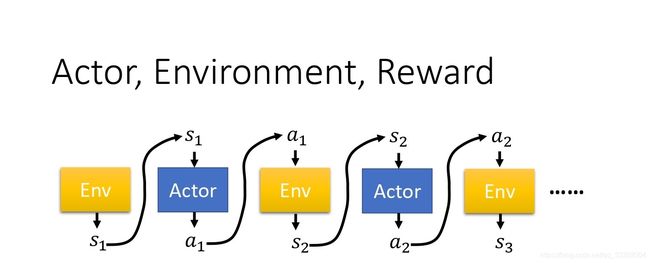
强化学习由三个组件构成：Actor、Environment、Reward Function。
Actor 决定如何执行下一个动作；
Environment 就是电脑主机或者对手会根据Actor的动作产生变化；
Reward Function 会根据我们做的动作进行打分。

在强化学习里面 Environment 和 Reward Function 都是不可操作的，我们的目标就是调整Actor的策略（Policy）获得最大的奖励期望。

• 一场游戏叫做一个 回合(episode) 或者 试验(trial)；

• 过程就是Env先初始化一个状态$s_1$，而后我们的Actor根据该初始状态做出动作;

• 产生一个Trajectory，我们用$\tau$表示，如下：
  $$\tau =\{s_1,a_1,s_2,a_2,...,s_t,a_t\}$$

2. Policy Network

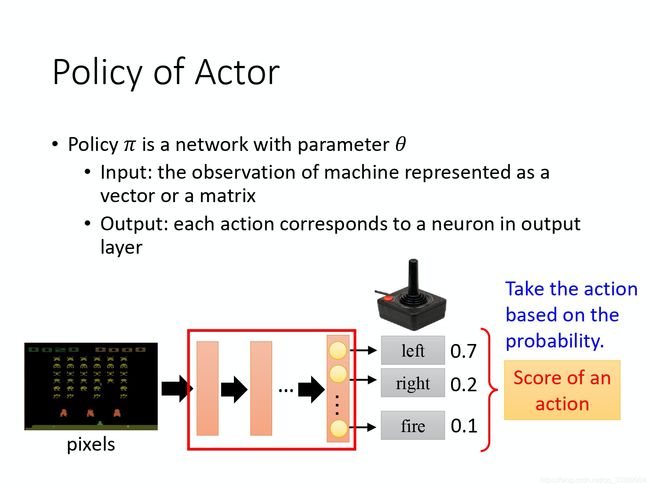
我们使用神经网络来完成动作的选择，以打电动游戏为例子：

我们有策略网络来实现策略$\pi$，网络的参数为$\theta$，输入为游戏的图像，输出的我们的操作。
在一场游戏中（一个episode），我们的Actor可以与环境交互产生一个回合的记录序列 Trajectory：
$$\tau =\{s_1,a_1,s_2,a_2,...,s_t,a_t\}$$
每一个$\tau$产生的概率为：
$$\begin{array}{rl}{p}_{\theta }(\tau )& =p(s_1)p_{\theta }(a_1|s_1)p(s_2|s_1,a_1)p_{\theta }(a_2|s_2)p(s_3|s_2,a_2)...\\ & =p(s_1)\prod _{t=1}^T{p}_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t)\end{array}$$
每一个$\tau$的总回报为：
$$R(\tau )=\sum _{t=1}^T{r}_t$$
我们的$\tau$是利用Actor与环境互动产生的，在动作选择过程中存在很多随机性，环境本身也存在很多随机性，所以$R(\tau )$是一个随机变量（random variable）。

所以我们不能用$R(\tau )$评价一个策略网络$\theta$的好坏，但是我们可以使用$R(\tau )$的期望评价：
$$\begin{array}{r}E[R(\tau )]=\bar{R}(\tau )=\sum _{\tau }R(\tau )p_{\theta }(\tau )=E_{\tau ～p_{\theta }(\tau )}[R(\tau )]\end{array}$$
因此我们的目标就是最大化（maximize）$\bar{R}(\tau )$，那么我们只需要朝着$\bar{R}(\tau )$梯度上升的方向调整参数$\theta$即可，
$$\begin{array}{rl}\nabla \bar{R}(\tau )& =\sum _{\tau }R(\tau )\nabla p_{\theta }(\tau )\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )\frac{\nabla p_{\theta }(\tau )}{p_{\theta }(\tau )}\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )\nabla log{p}_{\theta }(\tau )\\ & =E_{\tau ～p_{\theta }(\tau )}[R(\tau )\nabla log{p}_{\theta }(\tau )]\\ & \approx \frac{1}{N}\sum _{n=1}^{N}R(\tau )\nabla log{p}_{\theta }(\tau )\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R({\tau }^n)\nabla log{p}_{\theta }(a_t^n|s_t^n)\end{array}$$
直观理解这个梯度公式：我们知道在$s_t$状态下执行了$a_t$，如果最终的回报$R({\tau }^n)$是好的，那么就增加$(s_t|a_t)$的选择概率，否则减少。

3. Policy Network 训练过程如下：

• 先初始化一个策略网络$\theta$
• 用这个策略网络进行$N$次游戏，产生$N$个$\tau$（游戏记录）：
  $$\begin{gathered} {\tau }^1:\{s_1^1,a_1^1,s_2^1,a_2^1,...\},R({\tau }^1) \\ {\tau }^2:\{s_1^2,a_1^2,s_2^2,a_2^2,...\},R({\tau }^2) \\ ... \\ {\tau }^N:\{s_1^N,a_1^N,s_2^N,a_2^N,...\},R({\tau }^N) \end{gathered}$$
• 我们利用这$N$个$\tau$进行梯度上升，调整策略网络的参数：
  $$\begin{gathered} \nabla \bar{R}(\tau )=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R({\tau }^n)\nabla log{p}_{\theta }(a_t^n|s_t^n) \\ \theta \leftarrow \theta +\eta \nabla \bar{R}(\tau ) \end{gathered}$$
• 再如此重复2、3步。

4. 实现过程中的Tips

Tip 1： Add a Baseline

回顾一下我们的参数更新方法：
$$\theta \leftarrow \theta +\eta \nabla \bar{R}(\tau )$$

• 在许多问题中我们的回报$R(\tau )$没有负值，那么也就是说无论是否决策是否是好的，只要被采样到，都会提升被选中的概率。
• 如果我们的采样是无穷大的，那么这并不是个问题，但在实际中我们只能做到少量采样，那么没有被采样到的动作的选中概率就会一直下降，这样是不合理的。
• 所以我们要设计一种方法，让我们的reward不总是正值。
• 解决方法就是设置一个Baseline $b$，如果$R({\tau }^n)$大于$b$就让它的概率上升，否则就让概率下降，因此我们的梯度计算方法修正为：
  $$\nabla \bar{R}(\tau )=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}（R({\tau }^n)-b)\nabla log{p}_{\theta }(a_t^n|s_t^n)$$
• b的一个最简单的计算方法就是取本次采样的平均回报：
  $$b=E[R(\tau )]$$
• 在一些情况中会使用一个神经网络计算$b$

Tip 2： Assign Suitable Credit

上面我们将梯度的计算方法调整为：
$$\nabla \bar{R}(\tau )=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}（R({\tau }^n)-b)\nabla log{p}_{\theta }(a_t^n|s_t^n)$$
从公式中我们可以看出，在同一个episode里面，所有的$(s_t^n|a_t^n)$都具有相同的调整权重$（R({\tau }^n)-b)$，这显然是不合理的：

• 游戏结果是好的，不代表该场游戏中每一个决策都是好的；
• 游戏结果是坏的，不代表该场游戏中每一个决策都是坏的；

一种解决的思路是：

• 对于每一个$(s_t,a_t)$我们只计算该决策产生之后的反馈的累加；
• 因为这个决策并不会对之前的决策产生影响，所以之前决策的反馈值也不属于这个决策；
• 数学上就是做如下替换：
  $$R({\tau }^n)\leftarrow \sum _{t^{\prime }=t}^T{r}_{t^{\prime }}^n$$
• 也就是：
  $$\nabla \bar{R}(\tau )=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}（\sum _{t^{\prime }=t}^T{r}_{t^{\prime }}^n-b)\nabla log{p}_{\theta }(a_t^n|s_t^n)$$

我们继续观察现在的梯度公式，这里还存在一个问题，就是未来十分久远的决策的反馈并不一定受当前决策的影响：

• 我们在时刻2做的动作会影响时刻3的动作；
• 但我们在时刻2的动作对时刻1000的影响几乎为0，所以时刻1000产生的反馈不应该被加到时刻2中；
• 总结来说就是随着时间的推移，后面动作受前面动作的影响越来越小；
• 所以这里我们可以引入一个discount factor（衰减因子） $\gamma ,\gamma \in [0,1]$。
• 变换如下：
  $$R({\tau }^n)\leftarrow \sum _{t^{\prime }=t}^T{r}_{t^{\prime }}^n\leftarrow \sum _{t^{\prime }=t}^T{r}_{t^{\prime }}^n{\gamma }^{t^{\prime }-t}$$

所以最终的梯度公式如下：
$$\nabla \bar{R}(\tau )=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}（\sum _{t^{\prime }=t}^T{r}_{t^{\prime }}^n{\gamma }^{t^{\prime }-t}-b)\nabla log{p}_{\theta }(a_t^n|s_t^n),\gamma \in [0,1]$$

我们将$R-b$这一项定义为 Advantage function（比较优势） 符号表示为 $A^{\theta }(s_t,a_t)$：
$$A^{\theta }(s_t,a_t)=\sum _{t^{\prime }=t}^T{r}_{t^{\prime }}^n{\gamma }^{t^{\prime }-t}-b$$

• 表示：How good it is if we take $a_t$ other than actions at $s_t$.
• 也就是在$s_t$状态下，选择动作$a_t$，相比于选择其他动作有多大的优势；
• 它在意的不是一个绝对的好，而是相对的好；
• $A^{\theta }(s_t,a_t)$通常可以由一个网络估计出来，这个网络就是著名的A3C中的“critic”网络。