2000年数模B题 钢管订购和运输

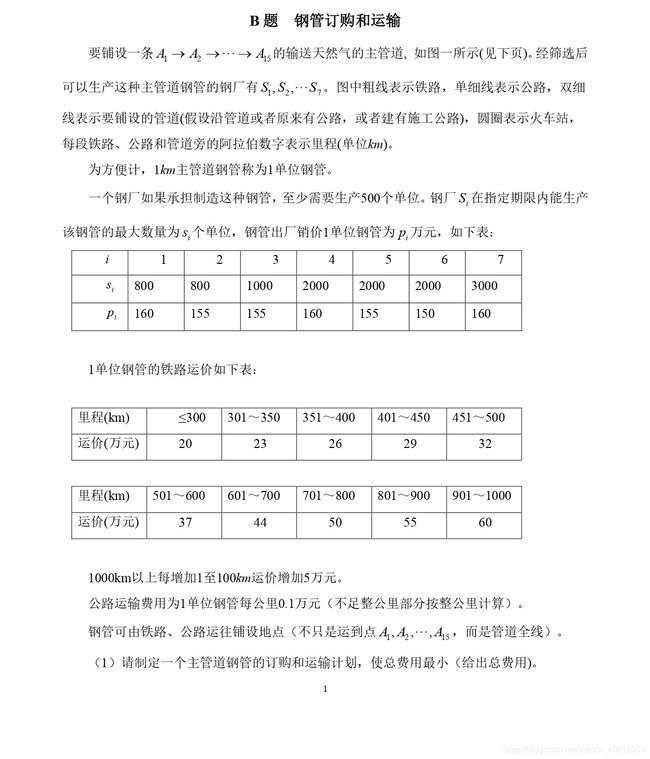
B 题 钢管订购和运输

解题思路

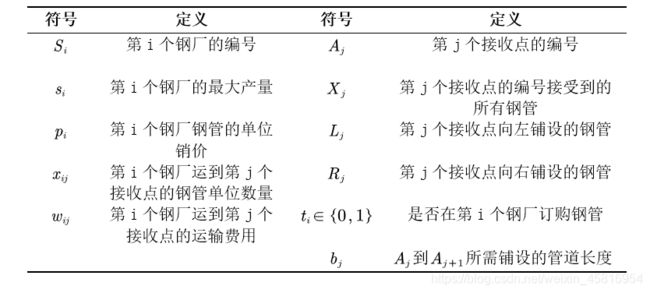
符号说明

第一问

这是一个运输规划问题，首先就是要求出第i个钢厂到第j个A地点的最小运费表如下图所示：

为了求出这个运费表，我们需要将题目中所给出的图转化成邻接矩阵的形式，由于铁路的运费随长度是分段变化的，而公路运费随长度线性变化。因此我们需要将铁路网和公路网分开计算每个交通网内部每个点之间的最短路径以及运输方案，这里可以用Floyd算法等来求。
然后根据铁路网和公路网的公共点来求出第i个钢厂到第j个A地点的最小运费表。

可以将总费用分为三部分：订购费用、运输费用和铺设费用，计算方式分别如下所示：
$$W_1=\sum _{i=1}^7\sum _{j=1}^{15}{p}_i{x}_{ij}$$
$$W_2=\sum _{i=1}^7\sum _{j=1}^{15}{w}_{ij}{x}_{ij}$$

上述分别为订购费用和铺设费用。
管道铺设是由一个点向两端铺设开来

$$A_j=L_j+R_j\left(j=\text{1,2,...,}15\right)$$
费用计算如下：
$$W_3=d\times \sum _{j=1}^{15}\left(\frac{L_j\left(L_j+1\right)}{2}+\frac{R_j\left(R_j+1\right)}{2}\right)$$

综合可列出总费用表达式：
$$W=\sum _{i=1}^7\sum _{j=1}^{15}{p}_i{x}_{ij}+\sum _{i=1}^7\sum _{j=1}^{15}{w}_{ij}{x}_{ij}+d\sum _{j=1}^{15}\left(\frac{L_j\left(L_j+1\right)}{2}+\frac{R_j\left(R_j+1\right)}{2}\right)$$

其必须满足产能限制、铺设计划限制和钢管必须用完限制，表示式如下所示：
$$\min W=\sum _{i=1}^7\sum _{j=1}^{15}{p}_i{x}_{ij}+\sum _{i=1}^7\sum _{j=1}^{15}{w}_{ij}{x}_{ij}+d\sum _{j=1}^{15}\left(\frac{L_j\left(L_j+1\right)}{2}+\frac{R_j\left(R_j+1\right)}{2}\right)$$
$$\{\begin{array}{c}{s}_i{t}_i\le {\sum }_{j=1}^{15}{x}_{ij}\le 500t_i\\ R_j+L_j={\sum }_{i=1}^7{x}_{ij}\\ R_j+L_{j+1}=b_j\\ t_i\in \left\{0,1\right\}\\ x_{ij},R_j,L_j\in \mathbb{Z}\\ x_{ij},R_j,L_j\ge 0\end{array}$$

对应的matlab数据处理程序如下所示：

%main函数
clear;clc;
% 铁路-中转初始邻接矩阵
D1 = xlsread('data.xlsx',1,'B2:Y25');

for i=1:size(D1,1)
   D1(i,i) = 0; 
end

line = isnan(D1);
[row, col] = find(line==1);

for i=1:length(row)
   D1(row(i),col(i)) = inf; 
end

[dist1,path1] = Floyd_algorithm(D1); %dist1返回最短路径长度，path1返回路径信息

print_path(path1, dist1, 19,1);

S = [7, 18, 19, 20, 22, 14, 17]; % 第i个钢厂的编号

S_t = zeros(7, 17); %钢厂-中转最短路径

for i = 1: size(S_t,1)
   for j =1:size(S_t,2)
      S_t(i,j) = dist1(S(i),j); 
   end
end

S_t_W = calc_wight(S_t);%钢厂-中转最少费用

% 中转-A初始邻接矩阵
D2 = xlsread('data.xlsx',4,'B2:AG33');

[row, col] = find(D2==0);

for i=1:length(row)
   D2(row(i),col(i)) = inf; 
end

for i=1:size(D2,1)
   D2(i,i) = 0; 
end


[dist2, path2] = Floyd_algorithm(D2); %dist2返回最短路径长度，path2返回路径信息

A = 18:32; % A地址编号

t_A = zeros(15,17); %中转-A最短路径

for i = 1: size(t_A,1)
   for j =1:size(t_A,2)
      t_A(i,j) = dist2(A(i),j); 
   end
end

t_A_W = t_A.*0.1;

[W,t] = calc_W(S_t_W,t_A_W); % W表示运费表，t表示中转点表

function [dist,path] = Floyd_algorithm(D)

n = size(D);
dist = D;

path = zeros(n);

for j =1:n
    path(:,j) = j;
end

for i = 1:n
    path(i,i) = -1;
end

for k = 1:n
    for i = 1:n
       for j = 1:n
           if dist(i,j) > dist(i,k)+dist(k,j)
               dist(i,j) = dist(i,k) + dist(k,j);
               path(i,j) = path(i,k);
               
           end
       end
    end
end

function print_path(path, dist, i,j)
if i==j
    disp(['从',num2str(i),'到',num2str(j),'的最短路径为']);
    disp([num2str(i),' ---> ',num2str(j)]);
    disp(['最短距离为',num2str(dist(i,j))]);
    return; 
end

if path(i,j) == j
    if dist(i,j) == inf
        disp(['从',num2str(i),'到',num2str(j),'没有路径可以到达'])
        
    else
        disp(['从',num2str(i),'到',num2str(j),'的最短路径为']);
        disp([num2str(i),' ---> ',num2str(j)]);
        disp(['最短距离为',num2str(dist(i,j))]);
    end
else
    k = path(i,j);
    result = [num2str(i),' ---> ']; 
    while k ~= j
        result = [result , num2str(k) , ' ---> ' ];
        k = path(k,j);
    end
     result = [result , num2str(k)];
    disp(['从',num2str(i),'到',num2str(j),'的最短路径为']);
    disp(result);
    disp(['最短距离为',num2str(dist(i,j))]);
end
    

function S_t_W = calc_wight(S_t)

W = xlsread('data.xlsx',2,'A1:C53');
S_t_W = zeros(size(S_t));

for i = 1:size(S_t,1)
   for j = 1:size(S_t,2)
      k = 1;
      while ~(S_t(i,j)>=W(k,1) & S_t(i,j)<=W(k,2))
          k = k+1;
      end
      S_t_W(i,j) = W(k,3);
   end
end

function [W,t] = calc_W(S_t_W,t_A_W)
W = zeros(7, 15);
t = zeros(7, 15);

for i = 1: 7
    for j = 1:15
        min1 = inf;
        min2 = 1;
        for k = 1: 17
            if min1 > (S_t_W(i,k)+t_A_W(j,k))
                min1 = S_t_W(i,k)+t_A_W(j,k);
                min2 = k;
            end
        end
        W(i,j) = min1;
        t(i,j) = min2;
    end
end

以上就可以得到第一问所需的一张运费表，然后就可以把问题转化成常规的运输问题来解决。

对应的lingo求解代码如下所示：

model:
sets:
stell_mill/1..7/:s,p,t;
scene/1..15/:L,R,b;
link(stell_mill,scene):w,x;


endsets

data:  
W,s,p,b = @ole("data.xlsx","W","S","P","b");
@ole("data.xlsx","result") = x;



enddata

[object] min = @sum(stell_mill(I): @sum(scene(J): p(I)*x(I,J))) + @sum(stell_mill(I): @sum(scene(J):w(I,J)*x(I,J))) + @sum(scene(J): 0.05*(R(J)*(R(J)+1)+L(J)*(L(J)+1)));


!产量限制条件;

!订单必须大于500个单位;
@for(stell_mill(I): [constrain_1]@sum(scene(J):x(I,J))>= 500*t(I));

!订单不能超过工厂产能;

@for(stell_mill(I): [constrain_2]@sum(scene(J):x(I,J))<=s(I)*t(I));

!钢管必须用完;

@for(scene(J): (R(J)+L(J)) = @sum(stell_mill(I):x(I,J)));

R(15) = 0;
L(1) = 0;

!钢管必须铺满;

@for(scene(J)|J #LT# 15: (R(J)+L(J+1)) = b(J));

@for(stell_mill: @bin(t));
@for(link: @gin(x));
@for(scene: @gin(R));
@for(scene: @gin(L));

求解结果：

第二问

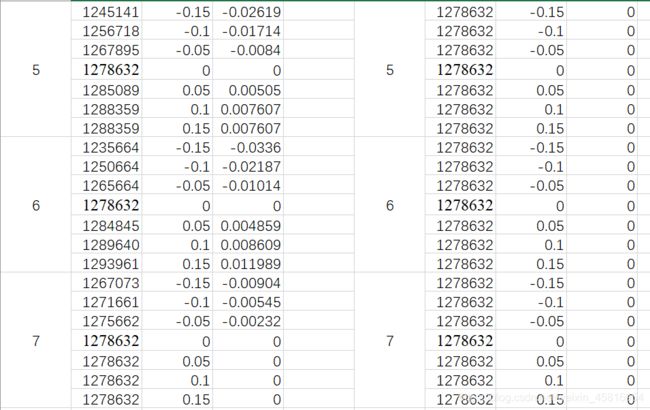
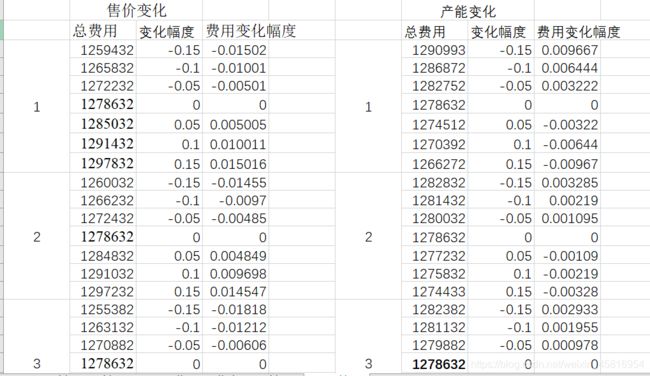
第二问就是对第一问的模型进行灵敏度分析我们可以对每个钢厂的钢管售价和产能进行上下15%的波动每个5%进行一次采样，分别得出对应的费用最小化数据如下所示：

然后对数据进行分析即可。

第三问

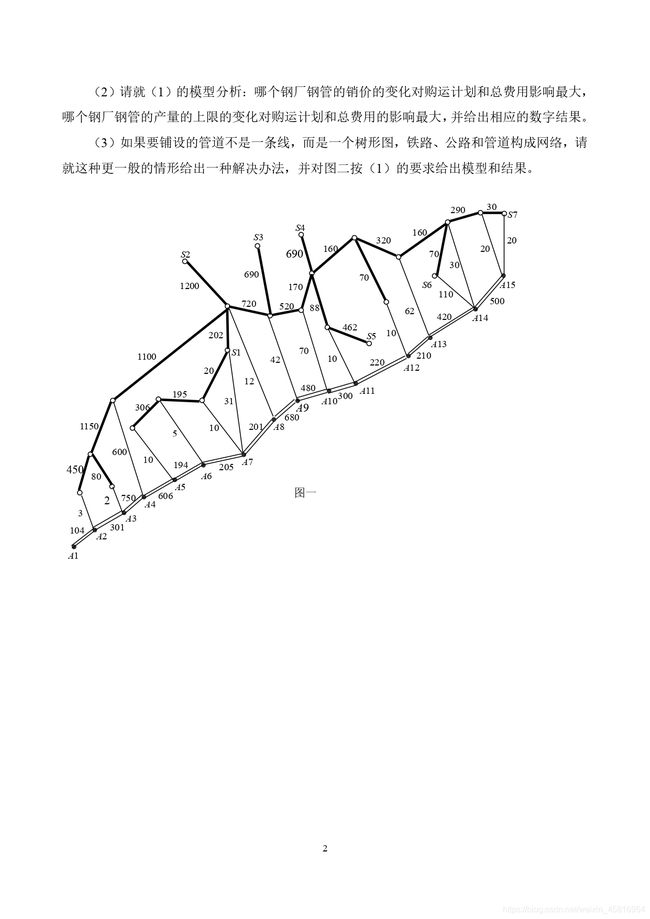
第三问在第一问的基础上要铺设的管道不是一条线，而是一个树形图，铁路、公路和管道构成网络。
对题目中的图二进行分析可得大部分的点和第一题是一样的，只有9、10、17三个点是有三个铺设方向的，因此可针对其做出单独约束，列出和第一问相似的目标函数和约束条件。
$$\min W=\sum _{i=1}^7\sum _{j=1}^{21}{p}_i{x}_{ij}+\sum _{i=1}^7\sum _{j=1}^{21}{w}_{ij}{x}_{ij}+d\sum _{\begin{array}{c}j=1\\ j\ne 9,11,17\end{array}}^{21}\left(\frac{L_j\left(L_j+1\right)}{2}+\frac{R_j\left(R_j+1\right)}{2}\right)$$
$$+d\sum _{j=9,11,17}\left(\frac{L_j\left(L_j+1\right)}{2}+\frac{R_j\left(R_j+1\right)}{2}+\frac{Z_j\left(Z_j+1\right)}{2}\right)$$
$$\{\begin{array}{c}{s}_i{t}_i\le {\sum }_{j=1}^{15}{x}_{ij}\le 500t_i\\ R_j+L_j={\sum }_{i=1}^7{x}_{ij}\left(j=1,2,...,8,10,12,...,21\right)\\ R_j+L_j+Z_j={\sum }_{i=1}^7{x}_{ij}\left(j=9,11,17\right)\\ R_j+L_{j+1}=b_j\left(j=1,2,...,14,17,19,20\right)\\ Z_{11}+L_{17}=b_{15}\\ Z_{17}+L_{19}=b_{16}\\ Z_9+L_{16}=b_{18}\\ t_i\in \left\{0,1\right\}\\ x_{ij},R_j,L_j\in \mathbb{Z}\\ x_{ij},R_j,L_j\ge 0\end{array}$$
第三问运费表：

利用lingo可求解得到结果

model:

sets:
stell_mill/1..7/:s,p,t;
scene/1..21/:L,R,Z,b;
link(stell_mill,scene):w,x;

endsets

data:
W,s,p,b = @ole("data_3.xlsx","W","S","p","b");
@ole("data_3.xlsx","result") = x;


enddata

[object] min = @sum(stell_mill(I): @sum(scene(J):p(I)*x(I,J))) + @sum(stell_mill(I):@sum(scene(J): w(I,J)*x(I,J))) + 0.05*(@sum(scene(J)|J #GE# 2: R(J)*(R(J)+1)) + @sum(scene(J)|J #LE# 14:L(J)*(L(J)+1)) + @sum(scene(J)|J #EQ# 9 #OR# J #EQ# 11 #OR# J #EQ# 17:Z(J)*(Z(J)+1)) + @sum(scene(J)|J#EQ#17 #OR# J#EQ#19 #OR# J#EQ#20:R(J)*(R(J)+1)));


!订单必须大于500个单位;

@for(stell_mill(I): @sum(scene(J): x(I,J)) >= 500*t(I));

!订单不能超过工厂产能;

@for(stell_mill(I): @sum(scene(J):x(I,J))<= s(I)*t(I));


!钢管必须用完;

@for(scene(J)|J#NE#9 #and# J#NE#11 #and# J #NE# 17:Z(J)=0);
@for(scene(J):L(J)+R(J)+Z(J)=@sum(stell_mill(I):x(I,J)));

!管道必须铺满;

@for(scene(J)| J #NE#15 #AND# J#NE#16 #AND# J #NE#18 #AND# J #LT#21:R(J)+L(J+1) = b(J));

b(15) = L(17)+Z(11);
b(16) = Z(17)+L(19);
b(18) = Z(9)+L(16);

@for(stell_mill: @bin(t));
@for(link: @gin(x));
@for(scene: @gin(R));
@for(scene: @gin(L));
@for(scene: @gin(Z));



end

求解结果：