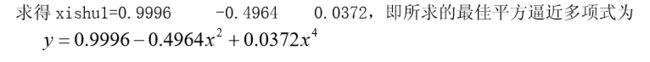插值与拟合 (二) ： 曲线拟合的线性最小二乘法
目录
1 线性最小二乘法
最小二乘准则 系数 
的确定
1.2 函数 
的选取
常用的拟合曲线：直线、多项式曲线、双曲线、指数曲线
2 最小二乘法的 Matlab 实现
2.1 解方程组方法
2.2 多项式拟合方法
a=polyfit(x0,y0,m) 用数据x0,y0拟合m 次多项式
y=polyval(a,x) 计算多项式在 x 处的值 y
3 最小二乘优化
3.1 lsqlin 函数 3.2 lsqcurvefit 函数
3.3 lsqnonlin 函数 3.4 lsqnonneg 函数
3.5 曲线拟合的用户图形界面求法
4 曲线拟合与函数逼近
函数逼近 最小平方逼近准则
正交多项式
勒让得（Legendre）多项式
第一类切比雪夫（Chebyshev）多项式 、拉盖尔（Laguerre）多项式
例：求最佳平方逼近多项式
建模分析: 黄河小浪底调水调沙问题
1 问题的提出
2 模型的建立与求解
插值与拟合习题
1 线性最小二乘法
曲线拟合问题的提法是，已知一组（二维）数据，即平面上的n个点 
, 
互不相同，寻求一个函数（曲线）
，使 
在某种准则下与所有数据点最为接近，即曲线拟合得最好。
最小二乘准则
系数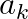 
的确定
1.2 函数 
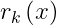的选取
常用的拟合曲线：直线、多项式曲线、双曲线、指数曲线
已知一组数据，用什么样的曲线拟合最好，可以在直观判断的基础上，选几种曲线 分别拟合，然后比较，看哪条曲线的最小二乘指标J 最小。
2 最小二乘法的 Matlab 实现
2.1 解方程组方法
例 4 用最小二乘法求一个形如 
的经验公式，使它与表 4 所示的数据 拟合。
解 编写程序如下
x=[19 25 31 38 44]';
y=[19.0 32.3 49.0 73.3 97.8]';
r=[ones(5,1),x.^2];
ab=r\y
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r') 2.2 多项式拟合方法
a=polyfit(x0,y0,m) 用数据x0,y0拟合m 次多项式
y=polyval(a,x) 计算多项式在 x 处的值 y
例 5 某乡镇企业 1990-1996 年的生产利润如表 5。 试预测 1997 年和 1998 年的利润。
解 作已知数据的的散点图，
x0=[1990 1991 1992 1993 1994 1995 1996];
y0=[70 122 144 152 174 196 202];
plot(x0,y0,'*')发现该乡镇企业的年生产利润几乎直线上升。因此，我们可以用 
作为 拟合函数来预测该乡镇企业未来的年利润。编写程序如下：
x0=[1990 1991 1992 1993 1994 1995 1996];
y0=[70 122 144 152 174 196 202];
a=polyfit(x0,y0,1)
y97=polyval(a,1997)
y98=polyval(a,1998) 
3 最小二乘优化
在无约束最优化问题中，有些重要的特殊情形，比如目标函数由若干个函数的平方和构成。这类函数一般可以写成：
最小二乘优化是一类比较特殊的优化问题，在处理这类问题时，Matlab 也提供了 一些强大的函数。在 Matlab 优化工具箱中，用于求解最小二乘优化问题的函数有：lsqlin、 lsqcurvefit、lsqnonlin、lsqnonneg，用法介绍如下。
3.1 lsqlin 函数
Matlab 中的函数为：
x=lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0) 例 6 用 lsqlin 命令求解例 4。
解 编写程序如下：
x=[19 25 31 38 44]';
y=[19.0 32.3 49.0 73.3 97.8]';
r=[ones(5,1),x.^2];
ab=lsqlin(r,y)
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r') 3.2 lsqcurvefit 函数
Matlab 中的函数为
X=LSQCURVEFIT(FUN,X0,XDATA,YDATA,LB,UB,OPTIONS)其中 FUN 是定义函数 F( x, xdata ) 的 M 文件。
function f=fun1(x,tdata);
f=x(1)+x(2)*exp(-0.02*x(3)*tdata); %其中 x(1)=a，x(2)=b，x(3)=k （2）调用函数 lsqcurvefit，编写程序如下：
td=100:100:1000;
cd=[4.54 4.99 5.35 5.65 5.90 6.10 6.26 6.39 6.50 6.59];
x0=[0.2 0.05 0.05];
x=lsqcurvefit(@fun1,x0,td,cd) 3.3 lsqnonlin 函数
Matlab 中的函数为
X=LSQNONLIN(FUN,X0,LB,UB,OPTIONS) 其中 FUN 是定义向量函数F( x)的 M 文件。
例 8 用 lsqnonlin 函数求解例 7。
解 这里
（1）编写 M 文件 fun2.m 如下：
function f=fun2(x);
td=100:100:1000;
cd=[4.54 4.99 5.35 5.65 5.90 6.10 6.26 6.39 6.50 6.59];
f=x(1)+x(2)*exp(-0.02*x(3)*td)-cd; （2）调用函数 lsqnonlin，编写程序如下：
x0=[0.2 0.05 0.05]; %初始值是任意取的
x=lsqnonlin(@fun2,x0) 3.4 lsqnonneg 函数
Matlab 中的函数为
X = LSQNONNEG(C,d,X0,OPTIONS) 
解 编写程序如下：
c=[0.0372 0.2869;0.6861 0.7071;0.6233 0.6245;0.6344 0.6170];
d=[0.8587;0.1781;0.0747;0.8405];
x=lsqnonneg(c,d) 3.5 曲线拟合的用户图形界面求法
Matlab 工具箱提供了命令 cftool，该命令给出了一维数据拟合的交互式环境。具体 执行步骤如下：
（1）把数据导入到工作空间；
（2）运行 cftool，打开用户图形界面窗口；
（3）对数据进行预处理；
（4）选择适当的模型进行拟合；
（5）生成一些相关的统计量，并进行预测。
可以通过帮助（运行 doc cftool）熟悉该命令的使用细节。
4 曲线拟合与函数逼近
函数逼近
最小平方逼近准则
正交多项式
勒让得（Legendre）多项式
第一类切比雪夫（Chebyshev）多项式 、拉盖尔（Laguerre）多项式
例：求最佳平方逼近多项式
解 编写程序如下：
syms x
base=[1,x^2,x^4];
y1=base.'*base
y2=cos(x)*base.'
r1=int(y1,-pi/2,pi/2)
r2=int(y2,-pi/2,pi/2)
a=r1\r2
xishu1=double(a) %系数
digits(8),xishu2=vpa(a) 
建模分析: 黄河小浪底调水调沙问题
1 问题的提出
2004 年 6 月至 7 月黄河进行了第三次调水调沙试验，特别是首次由小浪底、三门峡和万家寨三大水库联合调度，采用接力式防洪预泄放水，形成人造洪峰进行调沙试验获得成功。整个试验期为 20 多天，小浪底从 6 月 19 日开始预泄放水，直到 7 月 13 日 恢复正常供水结束。小浪底水利工程按设计拦沙量为 75.5 亿 
，在这之前，小浪底共积泥沙达 14.15 亿 t。这次调水调沙试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪，在小浪底形成人造洪峰，冲刷小浪底库区沉积的泥沙，在小浪底水库开闸泄洪以后，从 6 月 27 日开始三门峡水库和万家寨水库陆续开闸放水，人造洪峰于 29日先后到达小浪底，7 月 3 日达到最大流量 2700 
，使小浪底水库的排沙量也不断地增加。
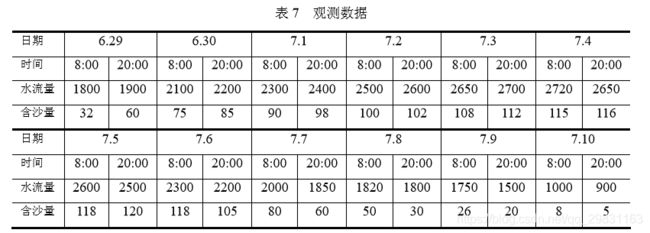
表 7 是由小浪底观测站从 6 月 29 日到 7 月 10 检测到的试验数据。
现在，根据试验数据建立数学模型研究下面的问题：
（1）给出估计任意时刻的排沙量及总排沙量的方法；
（2）确定排沙量与水流量的关系。
2 模型的建立与求解
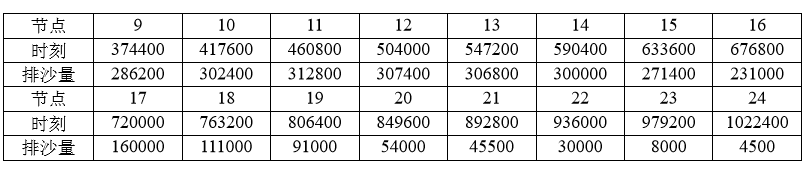
对于问题（1），根据所给问题的试验数据，要计算任意时刻的排沙量，就要确定出排沙量随时间变化的规律，可以通过插值来实现。考虑到实际中的排沙量应该是时间的连续函数，为了提高模型的精度，我们采用三次样条函数进行插值。
clc,clear
load data.txt %data.txt 按照原始数据格式把水流量和排沙量排成 4 行，12 列
liu=data([1,3],:); %水流量
liu=liu';liu=liu(:);
sha=data([2,4],:);
sha=sha';sha=sha(:); %排沙量
y=sha.*liu;y=y';
i=1:24;
t=(12*i-4)*3600;
t1=t(1);t2=t(end);
pp=csape(t,y);
xsh=pp.coefs %求得插值多项式的系数矩阵，每一行是一个区间上多项式的系数。
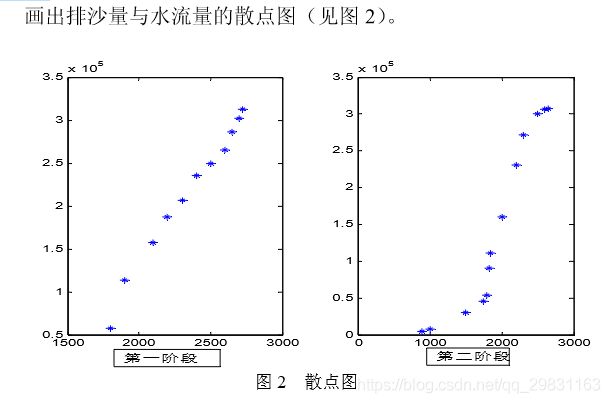
TL=quadl(@(tt)ppval(pp,tt),t1,t2) 
对于问题（2），研究排沙量与水流量的关系，从试验数据可以看出，开始排沙量是随着水流量的增加而增长，而后是随着水流量的减少而减少。显然，变化规律并非是线性的关系，为此，把问题分为两部分，从开始水流量增加到最大值 2720 （即增长的过程）为第一阶段，从水流量的最大值到结束为第二阶段，分别来研究水流量与排沙量的关系。
画散点图的程序如下：
load data.txt
liu=data([1,3],:);
liu=liu';liu=liu(:);
sha=data([2,4],:);
sha=sha';sha=sha(:);
y=sha.*liu;
subplot(1,2,1), plot(liu(1:11),y(1:11),'*')
subplot(1,2,2), plot(liu(12:24),y(12:24),'*') 
计算的 Matlab 程序如下：
clc, clear
load data.txt %data.txt 按照原始数据格式把水流量和排沙量排成 4 行，12 列
liu=data([1,3],:);
liu=liu'; liu=liu(:);
sha=data([2,4],:);
sha=sha'; sha=sha(:);
y=sha.*liu;
%以下是第一阶段的拟合
format long e
nihe1_1=polyfit(liu(1:11),y(1:11),1) %拟合一次多项式，系数排列从高次幂到低次幂
nihe1_2=polyfit(liu(1:11),y(1:11),2)
yhat1_1=polyval(nihe1_1,liu(1:11)); %求预测值
yhat1_2=polyval(nihe1_2,liu(1:11)); %以下求误差平凡和与剩余标准差
cha1_1=sum((y(1:11)-yhat1_1).^2); rmse1_1=sqrt(cha1_1/9)
cha1_2=sum((y(1:11)-yhat1_2).^2); rmse1_2=sqrt(cha1_2/8)
%以下是第二阶段的拟合
for j=1:3
str1=char(['nihe2_' int2str(j) '=polyfit(liu(12:24),y(12:24),' int2str(j+1) ')']);
eval(str1)
str2=char(['yhat2_' int2str(j) '=polyval(nihe2_' int2str(j) ',liu(12:24));']);
eval(str2)
str3=char(['cha2_' int2str(j) '=sum((y(12:24)-yhat2_' int2str(j) ').^2);'... 'rmse2_' int2str(j) '=sqrt(cha2_' int2str(j) '/(11-j))']);
eval(str3)
end
format
插值与拟合习题
4 ． （水箱水流量问题）许多供水单位由于没有测量流入或流出水箱流量的设备，而 只能测量水箱中的水位。试通过测得的某时刻水箱中水位的数据，估计在任意时刻（包括水泵灌水期间）t 流出水箱的流量 
。 给出原始数据表 11，其中长度单位为 E（1E＝30.24cm）。水箱为圆柱体，其直径 为 57E。 假设：
（1）影响水箱流量的唯一因素是该区公众对水的普通需要；
（2）水泵的灌水速度为常数；
（3）从水箱中流出水的最大流速小于水泵的灌水速度；
（4）每天的用水量分布都是相似的；
（5）水箱的流水速度可用光滑曲线来近似；
（6）当水箱的水容量达到 514×103g 时，开始泵水；达到 677.6×103g 时，便停止 泵水。
插值与拟合系列的两篇博文暂且更新到这里了，后面会再详细补充几个matlab拟合函数的参数信息。