论文笔记：SSD: Single Shot MultiBox Detector
一、基本信息
标题：SSD: Single Shot MultiBox Detector
时间：2016
引用格式：Liu, Wei, et al. “Ssd: Single shot multibox detector.” European conference on computer vision. Springer, Cham, 2016.
二、研究背景
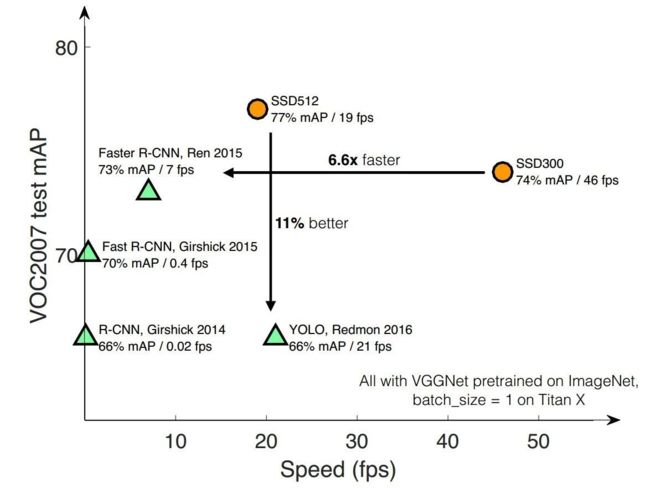
相比Faster RCNN有明显的速度优势，相比YOLO又有明显的mAP优势（不过已经被YOLO v2 超越）。
SSD的速度比Faster R-CNN快，主要是因为和yolo一样，把检测分为Single shot，同时加入了特征金字塔和其他优化，使得mPA又比yolo更快。
目标检测的主要方式
Two stages：
以Faster RCNN为代表，即RPN网络先生成proposals目标定位，再对proposals进行classification+bounding box regression完成目标分类。
R-CNN ：
输入->选取Proposals(使用SS方法)->卷积->bbox回归
Fast-R-CNN：
输入->卷积->选取Proposals(使用SS方法)->bbox回归
Faster-RCNN：
输入->卷积->选取Proposals(使用RPN：Anchors组合，进行初次bbox回归)->bbox再次回归
Single shot：
以YOLO/SSD为代表，一次性完成classification+bounding box regression。
YOLOv1：
提出和R-CNN不同的方式，去掉检测Proposal步骤，利用网格划分粗略位置，然后使用回归预测进行微调。虽然速度很快，但是每个网格只有2个bbox，召回率和准确度都不太高。
下面这些是在SDD之后发表的：
YOLOv2：
Better：
Batch normalization 批归一化 训练上的改进
High Resolution Classifier 高分辨率图像微调分类模型 训练上的改进
Convolutional With Anchor Boxes 采用先验框 借鉴Faster R-CNN中Anchor
Dimension Clusters 聚类提取先验框尺度 对Anchor的改进
Fine-Grained Features 检测细粒度特征 训练上的改进
Multi-Scale Training 多尺度图像训练 训练上的改进
Faster：
使用Darknet-19，更快
Stronger：
利用WordTree实现检测9000种对象
YOLOv3：
新的网络结构Darknet-53
利用多尺度特征进行对象检测 FPN
对象分类用Logistic取代了Softmax
尺度问题
橙色框代表图片，一般由resize/下采样操作产生；蓝色框代表特征图，通过卷积产生，越粗的框代表语义越深。
( a ) 多维度图片输入，多维度特征图预测：图像金字塔，不同尺寸的图输入到网络，底层分辨率高，可以检测细节，高层分辨率低，可以检测轮廓
( b ) 单维度图片输入，单维度特征图预测：拿单层(这里是最后一层)的特征图进行预测，Fast/er R-CNN R-CNN，YOLO v1v2都是这种
( c ) 单维度图片输入，多维度特征图预测：和b相比除了拿最后一层外，还会从后往前多拿几层预测，SSD使用这种方式(但是SSD使用低层的feature去检测小目标，而低级特征卷积层数少，存在特征提取不充分的问题。)
( d )单维度图片输入，多维度特征图预测：和c相比可以看到，本层会连接高层的语义，这样做的目的是使每一层不同尺度的特征图都具有较强的语义信息Mask RCNN、YOLO v3使用了这种方式
三、创新点
SSD具有如下主要特点：
从YOLO中继承了将detection转化为regression的思路，一次完成目标定位与分类
基于Faster RCNN中的Anchor，提出了相似的Prior box；
加入基于特征金字塔（Pyramidal Feature Hierarchy）的检测方式，即在不同感受野的feature map上预测目标
和YOLO1的对比
- SSD使用了金字塔结构，对于小物体检测，SSD更具体有优势
- YOLO在卷积层后接全连接层，SSD采用CNN直接进行检测
- SSD还加入了类似Anchor的Prior box(YOLO2也使用了Anchor )
为什么要金字塔结构？
作者认为仅仅靠同一层上的多个anchor来回归，还远远不够。因为有很大可能这层上所有anchor的IOU都比较小，就是说所有anchor离ground truth都比较远，用这种anchor来训练误差会很大。例如图2中，左边较低的层级因为feature map尺寸比较大，anchor覆盖的范围就比较小，远小于ground truth的尺寸，所以这层上所有anchor对应的IOU都比较小；右边较高的层级因为feature map尺寸比较小，anchor覆盖的范围就比较大，远超过ground truth的尺寸，所以IOU也同样比较小；只有图2中间的anchor才有较大的IOU。通过同时对多个层级上的anchor计算IOU，就能找到与ground truth的尺寸、位置最接近（即IOU最大）的一批anchor，在训练时也就能达到最好的准确度。
SSD从后面新增的卷积层中提取Conv7，Conv8_2，Conv9_2，Conv10_2，Conv11_2作为检测所用的特征图，加上Conv4_3层，共提取了6个特征图，其大小分别是 ( 38 , 38 ) , ( 19 , 19 ) , ( 10 , 10 ) , ( 5 , 5 ) , ( 3 , 3 ) , ( 1 , 1 ) (38,38),(19,19),(10,10),(5,5),(3,3),(1,1) (38,38),(19,19),(10,10),(5,5),(3,3),(1,1)
Prior box
类似Faster-RCNN中的Anchor
尺寸
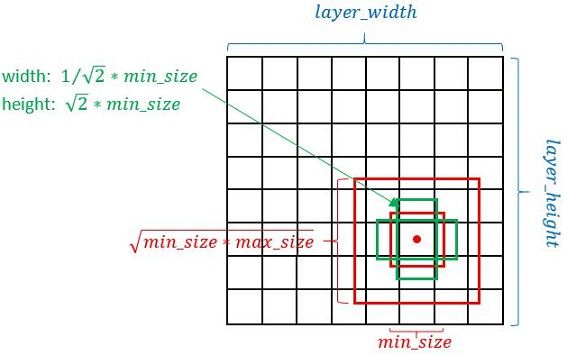
一般每个feature map点(单元)对应以该点为中心的6个Prior box(不同特征图设置的先验框数目不同)。上图显示了4个。而Faster RCNN默认为9个。
2个正方形：
小正方形边长： m i n _ s i z e min\_size min_size
大正方形边长： m i n − s i z e ∗ m a x − s i z e \sqrt{m i n_{-} s i z e * m a x_{-} s i z e} min−size∗max−size
(1~2) * 2 个长方形:
长方形长： a s p e c t _ − r a t i o ∗ m i n − s i z e \sqrt{aspect\_-ratio} *min_{-}size aspect_−ratio∗min−size
长方形宽： 1 / a s p e c t _ − r a t i o ∗ m i n _ s i z e 1 / \sqrt{aspect\_-ratio} * min\_size 1/aspect_−ratio∗min_size
要得到具体尺度还需要知道 m i n _ s i z e min\_size min_size、 m a x _ s i z e max\_size max_size、 a s p e c t _ − r a t i o aspect\_-ratio aspect_−ratio
是多少。
求 a s p e c t _ − r a t i o aspect\_-ratio aspect_−ratio:
一般 { 2 , 3 , 1 2 , 1 3 } \{2,3, \frac{1}{2}, \frac{1}{3}\} {2,3,21,31},但是在实现时，Conv4_3，Conv10_2和Conv11_2层仅使用4个先验框，它们不使用长宽比为 3 , 1 3 3, \frac{1}{3} 3,31 的先验框
求 s i z e size size:
先来看一个公式：
s k = s m i n + s m a x − s m i n m − 1 ( k − 1 ) , k ∈ [ 1 , m ] s_{k}=s_{m i n}+\frac{s_{m a x}-s_{m i n}}{m-1}(k-1), k \in[1, m] sk=smin+m−1smax−smin(k−1),k∈[1,m]
其中，paper中 s m i n = 0.2 s_{min} = 0.2 smin=0.2， s m a x = 0.9 s_{max} = 0.9 smax=0.9。上面公式 s m i n s_{min} smin、 s m a x s_{max} smax和 m m m固定，可以看成 y = b + k x y=b+kx y=b+kx线性模型。
s k s_{k} sk表示先验框大小相对于图片的比例。随着特征图大小降低，先验框尺度线性增加。
s i z e size size可以这么求，比如：
k = 1 k=1 k=1，即conv4_3
m i n _ s i z e = s 1 ∗ i n p u t _ s i z e min\_size = s_1 * input\_size min_size=s1∗input_size
m a x _ s i z e = s 2 ∗ i n p u t _ s i z e max\_size = s_2 * input\_size max_size=s2∗input_size
k = 2 k=2 k=2，即conv-7
m i n _ s i z e = s 2 ∗ i n p u t _ s i z e min\_size = s_2 * input\_size min_size=s2∗input_size
m a x _ s i z e = s 3 ∗ i n p u t _ s i z e max\_size = s_3 * input\_size max_size=s3∗input_size
…
k = 6 k=6 k=6，即conv11_2
m i n _ s i z e = s 6 ∗ i n p u t _ s i z e min\_size = s_6 * input\_size min_size=s6∗input_size
m a x _ s i z e = s 7 ∗ i n p u t _ s i z e max\_size = s_7 * input\_size max_size=s7∗input_size
这是论文中计算方式
但是在SSD300中prior box设置并不能完全和上述公式对应：
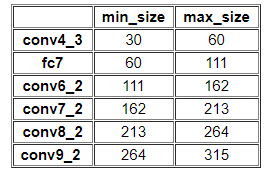可以简单描述为：
s 1 = s m i n / 2 s_1 = s_{min}/2 s1=smin/2
s k = s m i n + 0.17 ∗ ( k − 2 ) , k ∈ [ 2 , m ] s_k = s_{min} + 0.17 * (k-2), k \in[2, m] sk=smin+0.17∗(k−2),k∈[2,m]
0.17怎么来的？
⌊ ⌊ s max × 100 ⌋ − ⌊ s min × 100 ⌋ m − 1 ⌋ / 100 = 0.17 \left\lfloor\frac{\left\lfloor s_{\max } \times 100\right\rfloor-\left\lfloor s_{\min } \times 100\right\rfloor}{m-1}\right\rfloor/100= 0.17 ⌊m−1⌊smax×100⌋−⌊smin×100⌋⌋/100=0.17
如何使用、多层组合
以conv4_3和fc7为例分析SSD是如何将不同size的feature map组合在一起进行：
从左到右，从上往下梳理：
conv4_3 (1, 512, h_1, 2_1)：
conv4_3有4个prior box，所以下面可以看到很多地方乘4
经过conv4_3_norm不改变size和channel
1分支：经过一次batch norm+一次卷积后，生成了
[1, num_class*num_priorbox, layer_height, layer_width] 大小的feature用于softmax分类目标和非目标（其中num_class是目标类别，SSD300中num_class = 21，即20个类别+1个背景)。
由于SSD 300共有21个分类，所以conv4_3_norm_mbox_conf的channel值为num_priorbox * num_class = 4 * 21 = 84
2分支：经过一次batch norm+一次卷积后，生成了
[1, 4*num_priorbox, layer_height, layer_width] 大小的feature用于bounding box regression（即每个点一组[dxmin，dymin，dxmax，dymax]，参考Faster R-CNN 2.5节）
所以conv4_3_norm_mbox_loc的channel值为4 * 4 = 16；
1、2分支随后经过perm(Permute)层和flat(Flattlen)层。
Permute层是SSD中自带的层，相当于交换数据维度。即[batch_num, channel, height, width]变为[batch_num, height, width, channel]。
Flattlen层，就是拉成1维。
1分支当前层最后输出：(1,84w_1h_1)
2分支当前层最后输出：(1,16w_1h_1)
1、2分支再和其他层的输出进行connect。
1分支网络最后输出：(1,84w_1h_1 + 126w_2h_2 + 126w_3h_3 + 126w_3h_4 + 84w_5h_5+ 84w_6h_6)
2分支网络最后输出：(1,16w_1h_1 + 24w_2h_2 + 24w_3h_3 + 24w_3h_4 + 16w_5h_5+ 16w_6h_6)
3分支:生成了
[1, 2, 4num_priorboxlayer_height*layer_width] 大小的prior box blob，其中2个channel分别存储prior box的4个点坐标(x1, y1, x2, y2)和对应的4个参数variance(这实际上是一种bounding regression中的权重)
所以conv4_3_norm_priorbox的channel值为2，每个channel大小为4 * w_1*w _2*4
3分支当前层最后输出：(1,2,4 * w_1*w _2*4)
3分支网络最后输出：(1,2,4*w_1*h_1*4 + 4*w_2*h_2 *6+ 4*w_3*h_3*6 + 4*w_4*h_4 *6 + 4*w_5*h_5 *6+ 4*w_6*h_6 *4)
3分支的输出仅个人推导，具体要看论文代码怎么写的
fc7 (1, 1024, h_1, 2_1)：
和conv4_3类似。
主要过程就是下面这种图：
最后输出8732=(38*38*4+19*19*6 + .... + 1*1*4)个dectection，而yolo有98=(7 * 7 * 2)个dectection，进行NMS：
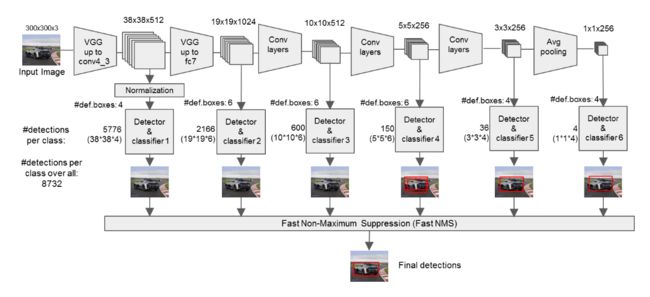
可以看到，SSD一次判断priorbox到底是背景 or 是20种目标类别之一，相当于将Faster R-CNN的RPN与后续proposal再分类进行了整合。
损失
loss函数分为两部分：计算相应的default box与目标类别的confidence loss以及相应的位置回归。
L ( x , c , l , g ) = 1 N ( L c o n f ( x , c ) + α L l o c ( x , l , g ) ) L(x, c, l, g)=\frac{1}{N}\left(L_{c o n f}(x, c)+\alpha L_{l o c}(x, l, g)\right) L(x,c,l,g)=N1(Lconf(x,c)+αLloc(x,l,g))
其中N是match到Ground Truth的default box数量；而alpha参数用于调整confidence loss和location loss之间的比例，默认alpha=1。
SSD中的confidence loss是典型的softmax loss：
L conf ( x , c ) = − ∑ i ∈ Pos N x i j p log ( c ^ i p ) − ∑ i ∈ Neg log ( c ^ i 0 ) where c ^ i p = exp ( c i p ) ∑ p exp ( c i p ) L_{\text {conf}}(x, c)=-\sum_{i \in \text {Pos}}^{N} x_{i j}^{p} \log \left(\hat{c}_{i}^{p}\right)-\sum_{i \in \text {Neg}} \log \left(\hat{c}_{i}^{0}\right) \quad \text { where } \quad \hat{c}_{i}^{p}=\frac{\exp \left(c_{i}^{p}\right)}{\sum_{p} \exp \left(c_{i}^{p}\right)} Lconf(x,c)=−i∈Pos∑Nxijplog(c^ip)−i∈Neg∑log(c^i0) where c^ip=∑pexp(cip)exp(cip)
其中， x i j p = { 1 , 0 } x_{i j}^{p}=\{1,0\} xijp={1,0}
代表第i个prior box匹配到了第j个class为p类别的GT box；而location loss是典型的smooth L1 loss：
L l o c ( x , l , g ) = ∑ i ∈ P o s N ∑ m ∈ { c x , c y , w , h } x i j k smooth L 1 ( l i m − g ^ j m ) L_{l o c}(x, l, g)=\sum_{i \in P o s}^{N} \sum_{m \in\{c x, c y, w, h\}} x_{i j}^{k} \operatorname{smooth}_{\mathrm{L} 1}\left(l_{i}^{m}-\hat{g}_{j}^{m}\right) Lloc(x,l,g)=i∈Pos∑Nm∈{cx,cy,w,h}∑xijksmoothL1(lim−g^jm)
其中：
g ^ j c x = ( g j c x − d i c x ) / d i w \hat{g}_{j}^{c x}=\left(g_{j}^{c x}-d_{i}^{c x}\right) / d_{i}^{w} g^jcx=(gjcx−dicx)/diw
g ^ j c y = ( g j c y − d i c y ) / d i h \hat{g}_{j}^{c y}=\left(g_{j}^{c y}-d_{i}^{c y}\right) / d_{i}^{h} g^jcy=(gjcy−dicy)/dih
g ^ j w = log ( g j w d i w ) \hat{g}_{j}^{w}=\log \left(\frac{g_{j}^{w}}{d_{i}^{w}}\right) g^jw=log(diwgjw)
g ^ j h = log ( g j h d i h ) \hat{g}_{j}^{h}=\log \left(\frac{g_{j}^{h}}{d_{i}^{h}}\right) g^jh=log(dihgjh)
Matching strategy：
在训练时，groundtruth boxes 与 default boxes（就是prior boxes） 按照如下方式进行配对：
- 首先，寻找与每一个ground truth box有最大的jaccard overlap(IoU)的default box，这样就能保证每一个groundtruth box与唯一的一个default box对应起来。
- SSD之后又将剩余还没有配对的default box与任意一个groundtruth box尝试配对，只要两者之间的jaccard overlap大于阈值，就认为match（SSD 300 阈值为0.5）。
- 显然配对到GT的default box就是positive，没有配对到GT的default box就是negative。
Hard negative mining：
值得注意的是，一般情况下negative default boxes数量>>positive default boxes数量，直接训练会导致网络过于重视负样本，从而loss不稳定。所以需要采取：
所以SSD在训练时会依据confidience score排序default box，挑选其中confidence高的box进行训练，控制 positive : negative = 1 : 3 =1: 3 =1:3
四、实验结果
五、结论与思考
作者结论
总结
思考
参考
SSD目标检测
目标检测|SSD原理与实现
解读SSD目标检测方法
目标检测之SSD
基于深度学习的目标检测算法：SSD——常见的目标检测算法
[目标检测]SSD原理