Ceres使用（三）

Powell’s Function

现在，考虑更复杂一点的情况，最小化Powell方程。令 x=[x1,x2,x3,x4] ，并且

f1(x)f2(x)f3(x)f4(x)F(x)=x1+10x2=5√(x3−x4)=(x2−2x3)2=10−−√(x1−x4)2=[f1(x),f2(x),f3(x),f4(x)]

F(x) 是一个有四个参数的方程，有四个残差，我们想要找到一个 x ，使得12∥F(x)∥2 最小。
第一步，定义评估目标函数项的函数。这里是评估 f4(x1,x4) 的代码：

struct F4 {
  template <typename T>
  bool operator()(const T* const x1, const T* const x4, T* residual) const {
    residual[0] = T(sqrt(10.0)) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
    return true;
  }
};

类似的，我们可以定义类F1，F2，F3来分别评估 f1(x1,x2) ， f2(x3,x4) 和 f3(x2,x3) 。使用这些，可以构造problem：

double x1 =  3.0; double x2 = -1.0; double x3 =  0.0; double x4 = 1.0;

Problem problem;

// Add residual terms to the problem using the using the autodiff
// wrapper to get the derivatives automatically.
problem.AddResidualBlock(
  new AutoDiffCostFunction1, 1, 1>(new F1), NULL, &x1, &x2);
problem.AddResidualBlock(
  new AutoDiffCostFunction1, 1, 1>(new F2), NULL, &x3, &x4);
problem.AddResidualBlock(
  new AutoDiffCostFunction1, 1, 1>(new F3), NULL, &x2, &x3)
problem.AddResidualBlock(
  new AutoDiffCostFunction1, 1, 1>(new F4), NULL, &x1, &x4);

注意，每个ResidualBlock只依赖于残差对应的两个参数，而不是全部四个参数。完整代码：

#include 
#include 
#include 
#include 
#include 

using namespace std;

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;

struct F1 {
    template <typename T>
            bool operator()(const T* const x1, const T* const x2, T* residual) const {
        residual[0] = x1[0] + T(10.0)*x2[0];
        return true;
    }
};

struct F2 {
    template <typename T>
            bool operator()(const T* const x3, const T* const x4, T* residual) const {
        residual[0] = T(sqrt(5.0))*(x3[0]-x4[0]);
        return true;
    }
};

struct F3 {
    template <typename T>
            bool operator()(const T* const x2, const T* const x3, T* residual) const {
        residual[0] = (x2[0]-T(2.0)*x3[0])*(x2[0]-T(2.0)*x3[0]);
        return true;
    }
};

struct F4 {
    template <typename T>
            bool operator()(const T* const x1, const T* const x4, T* residual) const {
        residual[0] = T(sqrt(10.0))*(x1[0]-x4[0])*(x1[0]-x4[0]);
        return true;
    }
};

DEFINE_string(minimizer, "trust_region",
              "Minimizer type to use, choices are: line_search & trust_region");

int main(int argc, char** argv) {
//    CERES_GFLAGS_NAMESPACE::ParseCommandLineFlags(&argc, &argv, true);
    google::InitGoogleLogging(argv[0]);

    double x1 =  3.0;
    double x2 = -1.0;
    double x3 = 0.0;
    double x4 = 1.0;

    // 建立Problem
    Problem problem;

    // 设置四个残差方程Fx，用自动求导获得导数（或者雅克比矩阵）
    // 自动求导的模板参数<误差类型， 输出维度， 输入维度>，如果输入有多个参数，就依次展开
    CostFunction* cost_function1 = new AutoDiffCostFunction1, 1, 1>(new F1);
    CostFunction* cost_function2 = new AutoDiffCostFunction1, 1, 1>(new F2);
    CostFunction* cost_function3 = new AutoDiffCostFunction1, 1, 1>(new F3);
    CostFunction* cost_function4 = new AutoDiffCostFunction1, 1, 1>(new F4);

    // 设置残差模块，参数（代价函数，核函数，待估计参数）
    problem.AddResidualBlock(cost_function1, NULL, &x1, &x2);
    problem.AddResidualBlock(cost_function2, NULL, &x3, &x4);
    problem.AddResidualBlock(cost_function3, NULL, &x2, &x3);
    problem.AddResidualBlock(cost_function4, NULL, &x1, &x4);

    // 设置求解器选项
    Solver::Options options;
    options.max_num_iterations = 100;
    options.linear_solver_type = ceres::DENSE_QR;   //增量方程的求解方式
    options.minimizer_progress_to_stdout = true;    //是否把最小二乘的优化过程输出到cout

    cout << "Initial x1 = "<< x1 << ", x2 = " << x2 << ", x3 = " << x3 << ", x4 = " << x4 << endl;

    Solver::Summary summary;    //优化信息
    Solve(options, &problem, &summary); //开始优化

    cout << summary.BriefReport() << endl;  //简要报告
    cout << summary.FullReport() << endl;   //完整报告
    cout << "Final x1 = " << x1 << ", x2 = " << x2 << ", x3 = " << x3 << ", x4 = " << x4 << endl;

    return 0;
}

对应的CMakeLists.txt文件：

cmake_minimum_required(VERSION 3.8)
project(ceres_study)

set(CMAKE_CXX_STANDARD 11)

find_package(Ceres REQUIRED)
include_directories( ${CERES_INCLUDE_DIRS} )

set(SOURCE_FILES powell.cpp)

add_executable(ceres_study ${SOURCE_FILES})
target_link_libraries(ceres_study ${CERES_LIBRARIES})

编译运行结果：

Initial x1 = 3, x2 = -1, x3 = 0, x4 = 1
iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  1.075000e+02    0.00e+00    1.55e+02   0.00e+00   0.00e+00  1.00e+04        0    5.84e-05    1.25e-04
   1  5.036190e+00    1.02e+02    2.00e+01   2.16e+00   9.53e-01  3.00e+04        1    7.50e-05    2.31e-04
   2  3.148168e-01    4.72e+00    2.50e+00   6.23e-01   9.37e-01  9.00e+04        1    4.01e-05    2.84e-04
   3  1.967760e-02    2.95e-01    3.13e-01   3.08e-01   9.37e-01  2.70e+05        1    3.73e-05    3.31e-04
   4  1.229900e-03    1.84e-02    3.91e-02   1.54e-01   9.37e-01  8.10e+05        1    3.58e-05    3.76e-04
   5  7.687123e-05    1.15e-03    4.89e-03   7.69e-02   9.37e-01  2.43e+06        1    3.09e-05    4.16e-04
   6  4.804625e-06    7.21e-05    6.11e-04   3.85e-02   9.37e-01  7.29e+06        1    2.85e-05    4.51e-04
   7  3.003028e-07    4.50e-06    7.64e-05   1.92e-02   9.37e-01  2.19e+07        1    2.82e-05    4.85e-04
   8  1.877006e-08    2.82e-07    9.54e-06   9.62e-03   9.37e-01  6.56e+07        1    2.82e-05    5.19e-04
   9  1.173223e-09    1.76e-08    1.19e-06   4.81e-03   9.37e-01  1.97e+08        1    2.93e-05    5.57e-04
  10  7.333425e-11    1.10e-09    1.49e-07   2.40e-03   9.37e-01  5.90e+08        1    2.81e-05    5.91e-04
  11  4.584044e-12    6.88e-11    1.86e-08   1.20e-03   9.37e-01  1.77e+09        1    3.06e-05    6.28e-04
  12  2.865573e-13    4.30e-12    2.33e-09   6.02e-04   9.37e-01  5.31e+09        1    3.53e-05    6.73e-04
  13  1.791438e-14    2.69e-13    2.91e-10   3.01e-04   9.37e-01  1.59e+10        1    3.40e-05    7.17e-04
  14  1.120029e-15    1.68e-14    3.64e-11   1.51e-04   9.37e-01  4.78e+10        1    3.90e-05    7.66e-04
Ceres Solver Report: Iterations: 15, Initial cost: 1.075000e+02, Final cost: 1.120029e-15, Termination: CONVERGENCE

Solver Summary (v 1.13.0-eigen-(3.2.0)-lapack-suitesparse-(4.2.1)-cxsparse-(3.1.2)-openmp)

                                     Original                  Reduced
Parameter blocks                            4                        4
Parameters                                  4                        4
Residual blocks                             4                        4
Residual                                    4                        4

Minimizer                        TRUST_REGION

Dense linear algebra library            EIGEN
Trust region strategy     LEVENBERG_MARQUARDT

                                        Given                     Used
Linear solver                        DENSE_QR                 DENSE_QR
Threads                                     1                        1
Linear solver threads                       1                        1
Linear solver ordering              AUTOMATIC                        4

Cost:
Initial                          1.075000e+02
Final                            1.120029e-15
Change                           1.075000e+02

Minimizer iterations                       15
Successful steps                           15
Unsuccessful steps                          0

Time (in seconds):
Preprocessor                         0.000067

  Residual evaluation                0.000023
  Jacobian evaluation                0.000394
  Linear solver                      0.000071
Minimizer                            0.000715

Postprocessor                        0.000005
Total                                0.000787

Termination:                      CONVERGENCE (Gradient tolerance reached. Gradient max norm: 3.642190e-11 <= 1.000000e-10)

Final x1 = 0.000146222, x2 = -1.46222e-05, x3 = 2.40957e-05, x4 = 2.40957e-05

可以看到，该问题的最优结果在 x1=0,x2=0,x3=0,x4=0 ，此时目标方程结果值为0。在第十次迭代中，Ceres计算得到的结果是 4×10−12 。

Curve Fitting

直到现在，我们看到的例子都是没有数据的简单优化问题。最小二乘法和非线性最小二乘法分析的最初目的是拟合数据曲线。现在就来考虑一个这样的例子，数据是由曲线 y=e0.3x+0.1 抽样生成的，再添加标准差为 σ=0.2 的高斯误差。让我们将一些数据拟合到曲线上：

y=emx+c

首先，定义一个模板对象来评估残差，对每一个观测值都会有一个残差。

struct ExponentialResidual {
  ExponentialResidual(double x, double y)
      : x_(x), y_(y) {}

  template <typename T>
  bool operator()(const T* const m, const T* const c, T* residual) const {
    residual[0] = T(y_) - exp(m[0] * T(x_) + c[0]);
    return true;
  }

 private:
  // Observations for a sample.
  const double x_;
  const double y_;
};

假设观测值是一个2n大小的数组，那么问题的构建就是为每个观测创建一个Cost函数。构建problem的代码：

double m = 0.0;
double c = 0.0;

Problem problem;
for (int i = 0; i < kNumObservations; ++i) {
  CostFunction* cost_function =
       new AutoDiffCostFunction1, 1, 1>(
           new ExponentialResidual(data[2 * i], data[2 * i + 1]));
  problem.AddResidualBlock(cost_function, NULL, &m, &c);
}

整个曲线拟合优化代码为：

#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;

struct ExponentialResidual {
    ExponentialResidual(double x, double y):x_(x), y_(y) {}

    template <typename T>
            bool operator()(const T* const m,   //待估参数m
                            const T* const c,   //待估参数c
                            T* residual) const {
        residual[0] = y_ - exp(m[0]*x_ + c[0]);
        return true;
    }

private:
    const double x_;  //x_, y_已知
    const double y_;
};

int main(int argc, char** argv)
{
    double m = 0.3, c = 0.1;    //生成数据集的准确值
    int N = 5;                  //x的最大值
    double sigma = 0.2;         //高斯噪声的标准差
    cv::RNG rng;                //OpenCV随机数生成器
    vector<double> x_data, y_data;

    // 生成随机数
    for(double i=0; i<=N ; i=i+0.075)
    {
        x_data.push_back(i);
        double yi = exp(m*i+c)+rng.gaussian(sigma);
        y_data.push_back(yi);
    }

    m = 0.0, c = 0.0;    //待估计值的初始值

    // 建立Problem
    Problem problem;

    // 对于每一对(x, y)都要添加残差模块
    for ( int i=0; i < x_data.size(); i++)
    {
        problem.AddResidualBlock(
                new AutoDiffCostFunction1, 1, 1>(new ExponentialResidual(x_data[i], y_data[i])),
                NULL,
                &m, &c);
    }

    cout << "Intial m = " << m << ", n = " << c << endl;

    // 设定求解选项
    Solver::Options options;
    options.max_num_iterations = 25;
    options.minimizer_progress_to_stdout = true;
    options.linear_solver_type = ceres::DENSE_QR;

    // 运行求解器
    Solver::Summary summary;
    Solve(options, &problem, &summary);
    cout << summary.BriefReport() << endl;
    cout << "Final m = " << m << ", n = " << c << endl;

    return 0;
}

对应的CMakelists.txt为：

cmake_minimum_required(VERSION 3.8)
project(ceres_study)

set(CMAKE_CXX_STANDARD 11)

# ceres
find_package(Ceres REQUIRED)
include_directories( ${CERES_INCLUDE_DIRS} )

# OpenCV
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_DIRS})

set(SOURCE_FILES curve_fitting.cpp)

add_executable(ceres_study ${SOURCE_FILES})
target_link_libraries(ceres_study ${CERES_LIBRARIES} ${OpenCV_LIBS})

编译运行结果：

Intial m = 0, n = 0
iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  1.204244e+02    0.00e+00    3.60e+02   0.00e+00   0.00e+00  1.00e+04        0    3.24e-04    3.74e-04
   1  2.425961e+03   -2.31e+03    0.00e+00   8.02e-01  -1.95e+01  5.00e+03        1    3.96e-05    4.64e-04
   2  2.422258e+03   -2.30e+03    0.00e+00   8.02e-01  -1.95e+01  1.25e+03        1    1.83e-05    5.08e-04
   3  2.400245e+03   -2.28e+03    0.00e+00   7.98e-01  -1.93e+01  1.56e+02        1    1.49e-05    5.34e-04
   4  2.210383e+03   -2.09e+03    0.00e+00   7.66e-01  -1.77e+01  9.77e+00        1    1.47e-05    5.59e-04
   5  8.483095e+02   -7.28e+02    0.00e+00   5.71e-01  -6.32e+00  3.05e-01        1    1.43e-05    5.84e-04
   6  3.404435e+01    8.64e+01    4.10e+02   3.12e-01   1.37e+00  9.16e-01        1    6.54e-04    1.25e-03
   7  7.242644e+00    2.68e+01    1.84e+02   1.27e-01   1.11e+00  2.75e+00        1    6.11e-04    1.97e-03
   8  3.933925e+00    3.31e+00    5.81e+01   3.45e-02   1.03e+00  8.24e+00        1    5.71e-04    2.64e-03
   9  2.333679e+00    1.60e+00    2.52e+01   9.77e-02   9.90e-01  2.47e+01        1    3.54e-04    3.02e-03
  10  1.419436e+00    9.14e-01    8.73e+00   1.16e-01   9.83e-01  7.42e+01        1    3.44e-04    3.38e-03
  11  1.245322e+00    1.74e-01    1.43e+00   6.69e-02   9.89e-01  2.22e+02        1    3.45e-04    3.74e-03
  12  1.237976e+00    7.35e-03    9.21e-02   1.61e-02   9.91e-01  6.67e+02        1    3.42e-04    4.10e-03
  13  1.237935e+00    4.11e-05    9.96e-04   1.28e-03   9.90e-01  2.00e+03        1    3.40e-04    4.46e-03
Ceres Solver Report: Iterations: 14, Initial cost: 1.204244e+02, Final cost: 1.237935e+00, Termination: CONVERGENCE
Final m = 0.301681, n = 0.0907709

从参数 m=0，c=0 开始，目标方程值的结果最开始为120.424，Ceres找到的结果是 m=0.301681,n=0.0907709 ，此时目标方程值为1.2379。参数值的优化结果和原来模型的 m=0.3,c=0.1 有一点不同，但这是意料之中的。当从噪声数据中重建曲线时，我们期望看到这样的偏差。事实上，如果要评估 m=0.3,c=0.1 的目标函数，那么目标函数值为1.237935。最后的拟合曲线如下图所示：

Robust Curve Fitting

现在，假设给出的数据中含有异常点，也即有一些点并不遵从噪声模型。如果我们使用上面的代码区拟合曲线，我们将会得到下面的曲线，拟合曲线会偏离真值曲线。

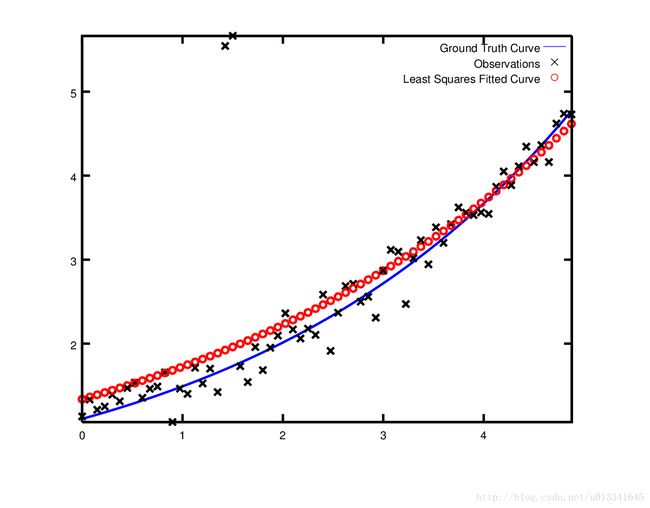
为了处理异常点，标准做法是使用一个损失函数LossFunction。损失函数减少了较大残差值对残差块的影响，通常是对应于异常点。为了在残差块中使用损失函数，我们修改以下代码：

problem.AddResidualBlock(cost_function, NULL , &m, &c);

为

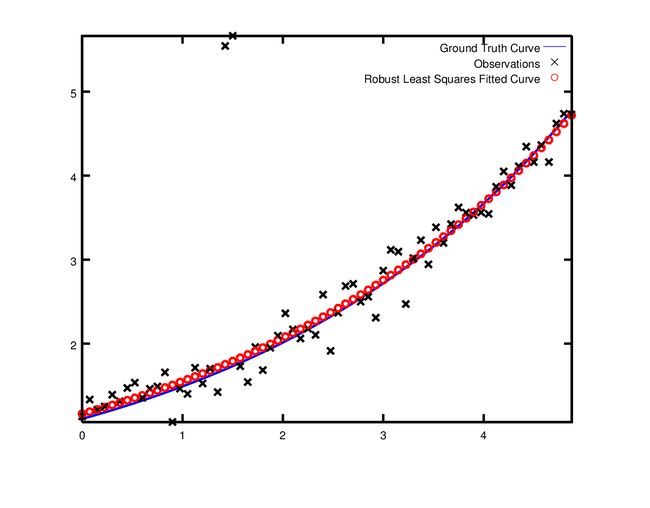
problem.AddResidualBlock(cost_function, new CauchyLoss(0.5) , &m, &c);

CauchyLoss是Ceres求解器的损失函数之一。0.5指定了损失函数的大小。结果，我们可以得到下面的拟合图。注意，拟合曲线和真值曲线已经很接近了。