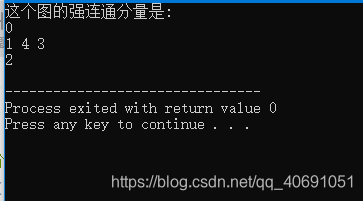
打印有向图的强连通分量-----kosaraju算法(最简单的实现)
一、kosaraju算法步骤:
1、首先对图G进行一次DFS,记录每个顶点完成的顺序(DFS树/林的叶子节点先完成,然后回溯到它双亲这一层,它个双亲递归遍历完自己的邻居并在这些递归完成回溯到这层后,它自己也完成了。
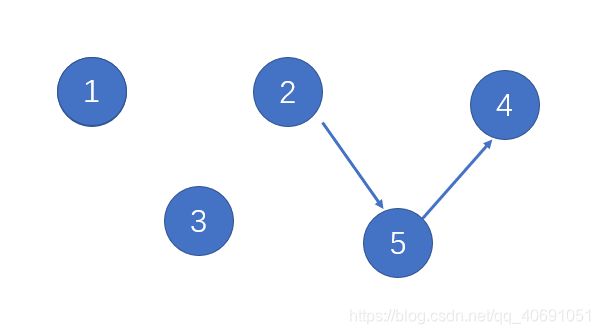
如这个图:假设从1开始DFS:
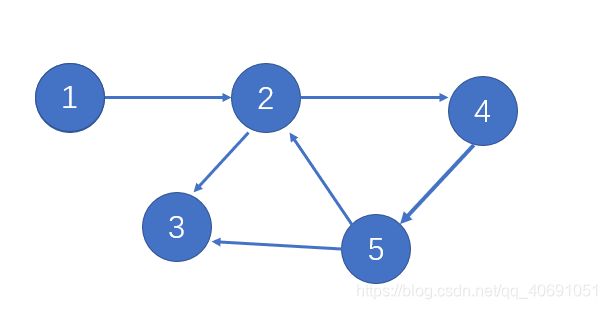
假设它的DFS生成树是这个:
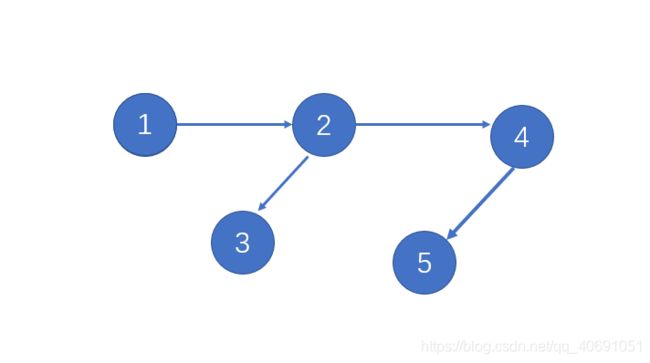
那么各顶点的完成的顺序是:3,5,4,2,1
2、把图G所有的边方向,得到G',沿步骤1得到顺序,从最后完成那割顶点开始,再次对每个顶点(如果它没有被访问过)进行DFS,这样如果整个图不是一个强连通图,那就会得到一个DFS森林,其中每颗DFS生成树都是一个强连通分量。
例如上面图反向后:
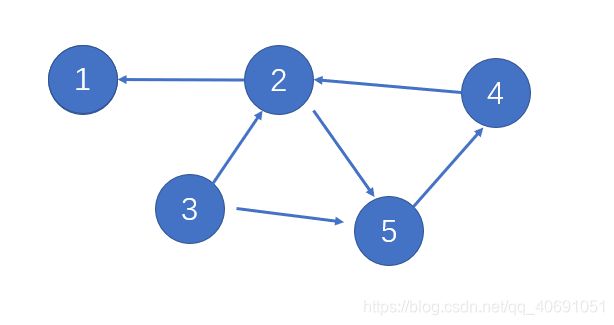
按第一次对原图DFS遍历得到的各顶点的完成顺序相反的顺序,对反转后的图再次DFS,得到的就是这个森林:
二、证明:
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/GraphAlgor/strongComponent.htm
排版好差,我也看不懂。
三、代码:
1、图:
#include<iostream>
#include<list>
#include<stack>
#define NIL -1
using namespace std;
class Graph
{
int n;
list<int> *adj;
void getOrder(int u,bool visited[],stack<int> &stk);
void DFSUtil(int u, bool visited[]);
public:
Graph(int _n){ n = _n; adj = new list<int>[_n]; }
~Graph(){ delete [] adj; }
void addEdge(int v, int w){ adj[v].push_back(w); }
Graph getTranspose();
void printSCCs();
};
2、获得反向图:
Graph Graph::getTranspose() //有向图反向
{
Graph g(n);
list<int>::iterator it;
for(int i = 0; i < n; i++)
{
for(it = adj[i].begin(); it != adj[i].end(); it++)
{
g.addEdge(*it,i);
}
}
return g;
}
3、获得完成的顺序,因为在对反向图进行DFS的时候,是按完成顺序相反的顺序进行的,所以可以用栈进行存储,最先完成的会在栈底,最后完成的会在栈顶。
void Graph::getOrder(int u, bool visited[],stack<int>&stk)
{//对原图DFS,用栈记录完成顺序,最后完成的会在栈顶
visited[u] = true;
list<int>::iterator it;
for(it = adj[u].begin(); it != adj[u].end(); it++)
{
if(!visited[*it])
{
getOrder(*it, visited,stk);
}
}
stk.push(u); //完成后用栈记录
}
void Graph::DFSUtil(int u, bool visited[])
{
visited[u] = true;
cout<<u<<" "; //打印
list<int>::iterator it;
for(it = adj[u].begin(); it != adj[u].end(); it++)
{
if(!visited[*it])
{
DFSUtil(*it,visited);
}
}
}
void Graph::printSCCs()
{
bool *visited = new bool[n];
stack<int>stk;
for(int i = 0; i < n; i++)
{
visited[i] = false;
}
getOrder(0, visited, stk); //获得顺序
for(int i = 0; i < n; i++)
{
visited[i] = false;
}
Graph gr = getTranspose(); //获得反向的图
while(!stk.empty())
{//对反向图进行DFS,按于第一次DFS时各点完成访问相反的顺序进行
int v = stk.top();
stk.pop();
if(!visited[v])
{
gr.DFSUtil(v,visited);
cout<<endl; //用换行符分隔强连通分量
}
}
}
四、测试:
#include<iostream>
#include<list>
#include<stack>
#define NIL -1
using namespace std;
class Graph
{
int n;
list<int> *adj;
void getOrder(int u,bool visited[],stack<int> &stk);
void DFSUtil(int u, bool visited[]);
public:
Graph(int _n){ n = _n; adj = new list<int>[_n]; }
~Graph(){ delete [] adj; }
void addEdge(int v, int w){ adj[v].push_back(w); }
Graph getTranspose();
void printSCCs();
};
//获得反向图:
Graph Graph::getTranspose() //有向图反向
{
Graph g(n);
list<int>::iterator it;
for(int i = 0; i < n; i++)
{
for(it = adj[i].begin(); it != adj[i].end(); it++)
{
g.addEdge(*it,i);
}
}
return g;
}
//获得完成的顺序,因为在对反向图进行`DFS`的时候,是按完成顺序相反的顺序进行的,
//所以可以用栈进行存储,最先完成的会在栈底,最后完成的会在栈顶。
void Graph::getOrder(int u, bool visited[],stack<int>&stk)
{//对原图DFS,用栈记录完成顺序,最后完成的会在栈顶
visited[u] = true;
list<int>::iterator it;
for(it = adj[u].begin(); it != adj[u].end(); it++)
{
if(!visited[*it])
{
getOrder(*it, visited,stk);
}
}
stk.push(u); //完成后用栈记录
}
void Graph::DFSUtil(int u, bool visited[])
{
visited[u] = true;
cout<<u<<" "; //打印
list<int>::iterator it;
for(it = adj[u].begin(); it != adj[u].end(); it++)
{
if(!visited[*it])
{
DFSUtil(*it,visited);
}
}
}
void Graph::printSCCs()
{
bool *visited = new bool[n];
stack<int>stk;
for(int i = 0; i < n; i++)
{
visited[i] = false;
}
getOrder(0, visited, stk); //获得顺序
for(int i = 0; i < n; i++)
{
visited[i] = false;
}
Graph gr = getTranspose(); //获得反向的图
while(!stk.empty())
{//对反向图进行DFS,按于第一次DFS时各点完成访问相反的顺序进行
int v = stk.top();
stk.pop();
if(!visited[v])
{
gr.DFSUtil(v,visited);
cout<<endl; //用换行符分隔强连通分量
}
}
}
int main()
{
Graph g(5);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(3, 4);
g.addEdge(4, 1);
g.addEdge(4, 2);
cout << "这个图的强连通分量是:"<<endl;
g.printSCCs();
return 0;
}
Tarjan算法