优化模型：钢管订购及运输优化模型

一、问题重述

要铺设一条输送天然气的主管道：A1→A2→…→A15，
能生产这种钢管的厂家一共有：S1,S2,…,S7。
厂家与管道间的交通网络已知。粗线表示铁路，单细线表示公路，双细线表示要铺设的管道（假设沿着管道或者原来有公路，或者建有施工公路）
一个钢厂如果承担制造这种钢管，至少需要生产 500 个单位。钢厂S_i在指定期限内能生产 该钢管的最大数量为s_i个单位，钢管出厂销价1单位钢管为p_i万元。如下表。
1单位钢管的铁路运价如下表，另外1000km以上每增加1至100km运价增加5万元。
公路运输费用为1单位钢管每公里0.1万元（不足整公里部分按整公里计算）。
钢管可由铁路、公路运往铺设地点（不只是运到主管道结点A₁,A₂,…,A₁₅，而是管道全线）。

需要解决的问题

（1）请定制一个主管道钢管的订购和运输计划，使总费用最小（给出总费用）。
（2）请就（1）的模型分析：哪个钢厂钢管的销量的变化对运购计划和总费用影响最大，哪个钢厂钢管的产量的上限的变化对购运计划和费用的影响最大，并给出相应的数字结果。
（3）如果要铺设的管道不是一条直线，而是一个树形图，铁路、公路和管道构成的网络，请就这种更一般的情况给出一种解决办法，并对图（2）的情形给出模型结果。

二、模型假设

1. 铺设的主管道以有公路或者有施工公路。
2. 在主管道上，每公里卸1单位的钢管。
3. 公路运输费用为1单位钢管每公里0.1万元（不足整公里部分按整公里计算）
4. 在计算总费用时，只考虑运输费和购买钢管的费用，而不考虑其他费用。
5. 在计算钢厂的产量对购运计划的影响时，只考虑钢厂的产量足够满足需要的情况，即钢厂的产量不受限制。
6. 假设钢管在铁路运输路程超过1000km时，铁路每增加1至100km，1单位钢管的运价增加5万元。

三、符号说明

$S_i：第i个钢厂；i=1,2,...,7$
$s_i:第i个钢厂的最大产量；i=1,2,...,7$
$A_j:输送管道（主管道）上的第j个点；j=1,2,...,15$
$p_i：第i个钢厂1单位钢管的销价；i=1,2,...,7$
$x_{ij}:钢厂S_i向点A_j运输的钢管量；i=1,2,...,7j=1,2,...,15$
$y_j:在点A_j与点A_{j+1}之间的公路上，运输点A_j向点A_{j+1}方向铺设的钢管量；j=1,2,3,...,14$
$A_{ij}:1单位钢管从钢厂S_i到点A_j的最少总费用，即公路运费、铁路运费和钢管销价之和；i=1,2,...,7j=1,2,...,15$

四、模型的分析、建立、求解

1. 模型的分析与决策变量的设置

先看总费用：总费用由三部分组成：
1.钢管的订购费。
2.运费。
3.铺设费用。
再看订购和运输计划：
所谓订购计划：就是向每个钢厂订购多少钢管。
所谓运输计划：就是将每个钢厂订购的钢管运输到那些结点？运多少？

$故可设：向第i个钢厂订购x_i单位的钢管，第i个钢厂运往第j个结点x_{ij}单位的钢管。$
$i=1,2,...,7j=1,2,...,15$

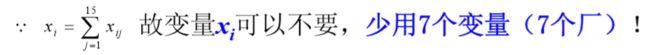再决定每个结点分别向左右铺设多少
当钢管从钢厂S_i运到点A_j后，钢管就要向运输点A_j的两边A_jA_j+1段和A_j-1A_j段运输（铺设）管道。
设y_i是结点A_j向右铺设与A_j+1向左铺设之间的交点（y₁=0，y₁₅=0）。（j=2,3,…,14）

2.模型的建立

1）目标函数

总费用=铺设总费用+成本及运输总费用=C+W

(1)铺设总费用

当钢管从钢厂运到点A_j后，钢管就要向运输点A_j的两边A_jA_j+1端和A_j-1A_j段运输（铺设）管道。
y_j：表示结点A_j到A_j+1之间的分界点（y₁=0，y₁₅=0），铺设方法如下图：
$设A_j向A_j{A}_{j+1}段的运输费为0.1\times (1+2+...+y_j)=\frac{y_j(y_j+1)}{20};由于相邻运输点A_j与A_{j+1}之间的距离为d_j，那么A_{j+1}向A_j{A}_{j+1}段铺设的管道长为d_j-y_j，所以对应铺设的费用为\frac{(d_j-y_j+1)(d_j+y_j)}{20}$。
故总的铺设费用为：

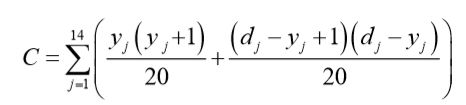
注意变量j的取值是从1到14，不取0和15。

(2)成本和运输总费用

$若运输点A_j向钢厂S_i订购x_{ij}单位钢管，A_{ij}是1单位钢管从钢厂S_i到点A_j的最少总费用，即公路运费、铁路运费和钢管销价之和；则钢管从钢厂S_i运到运输点A_j所需的费用为A_{ij}{x}_{ij}$
由于钢管运到A₁必须经过A₂，所以可以不考虑A₁，那么所有钢管从钢厂运到各个运输点上的总费用为：
目标函数为：
综合上述分析，得非线性规划模型：

(3)求单位钢管从钢厂运到运输点的最小费用A_ij

方法：将图一转换为一个以单位钢管的运输费 用为权的赋权图，再求最短路的权.
由于运输过程中既有铁路，也有公路。 铁路的运费还是分段函数，与全程运输总距离有 关；各路运费却是线性函数。

在数学建模中，时常会出现最短路问题。
最短路问题是指：若从图中的某一顶点(源点) 到达另一顶点(终点)的路径不止一条，如何寻找 一条路径，使得沿此路径各边上的权值总和(源点 到终点的距离)最小，这条路径称为最短路径。
许多优化问题都等价于在一个图中寻找最短路。 例如，管道的铺设、线路的安排、厂址的选取和 布局、设备的更新等。

定义：若将图G的每一条边e都对应一个实数w(e)，称w(e)为边的权， 并称图G为赋权图.

思路： 由于钢厂S_i直接与铁路相连，所以可先求出钢厂S_i到铁路与公路相交点b_j（对应于A_j）的最短路径。

1. 将铁路图转化成费用图

将铁路与公路交界的点编号 b_j

计算S_i到b_i的最小费用

2.合并铁路和公路图得以费用为权的交通网络图

思路：①再将与b_j相连的公路、运输点A_i及其与之相连的要铺设管 道的线路（也是公路）添加到图上。
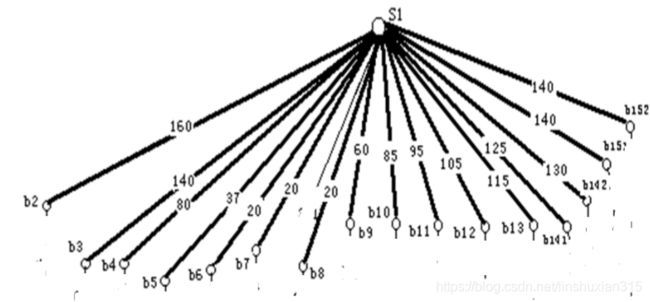
②同时根据单位钢管在公路上的运价规定，得出每一段公路的 运费，并把此费用作为边权赋给相应的边。以S₁为例得图：

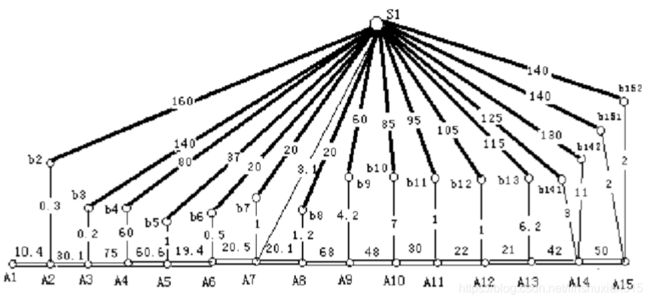
3.计算S₁到结点A_i的最小费用

再用图论软件包或MATLAB或LINGO求解,如S₁到A_i的最小费用（万元）为:

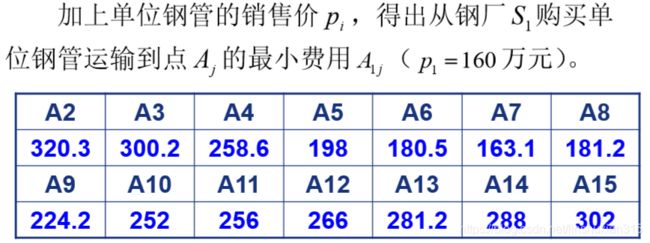
4.计算单位钢管从S₁到A_i的订购与运输的最小费用

5.从S_i购买单位钢管运到结点A_i的最小费用A_ij

同理，可用同样的方法求出钢厂S₂、S₃、S₄、S₅、S₆、S₇到点A_j的最小费用，从而得出从钢厂S_i购买单位钢管运到结点A_j的最小总费用 A_ij（单位：万元）为：

3.模型的求解

用LINGO求解（gangguan）:

不让S₇生产的模型：
要求钢厂S7的产量不小于500个单位的模型