模糊C均值聚类算法

  学习了一下模糊聚类中的模糊 C 均值聚类算法 (Fuzzy C-Means Clustering)。

  Fuzzy 意为模糊，其中包括几种模糊的方式，这里使用的是最简单的方式，它是基于概率的概念。我们把每一个点属于每一类的概率值求出，它属于哪一类别的概率最大，我们就将其归于哪一类。

  这里的 C 其实对应于 K-means 中的 K。其中，K-means 中的 K 决定类别数。同样的，C 也是决定类别数。

  首先我们介绍该算法的目标函数。

  当分类时，我们希望类内距离要越小越好（越集中越好），类与类之间的距离要越大越好。而 Fuzzy C-Means 只用到第一个概念 (类内距离要越小越好)。如果我们同时考虑类与类之间的距离，那么分类效果自然会得到提升。所以还有很多种不同的方式。

  下图中，假设红星是 $c_1$ 的中心，黄星是 $c_2$ 的中心。
      
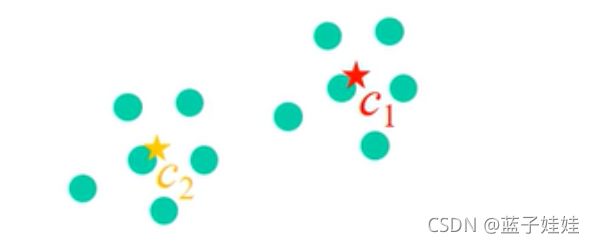
  我们给每一个点赋予到每一个类别中心的几率值，如下图中，$x_j$ 到 $c_1$ 中心点的几率值为 $u_{1j}$，其中 1 表示类别数，j 表示哪一个点。我们将 $u_{1j}$ 称为隶属值 (membership values)，代表点 j 隶属于第一类概率是多少。
      
  那么，也就有点 $j$ 隶属于第2类的概率 $u_{2j}$。
      
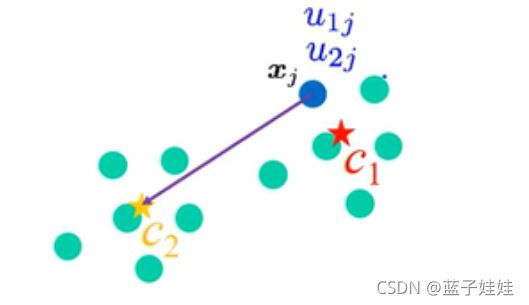
  依次类推，如果有 3 类，点 $j$ 就有 3 个隶属值；有 $n$ 类，就有 $n$ 个隶属值。并且需要满足 $u_{1j}+u_{2j}+\cdots +u_{nj}=1$，例子中为 $u_{1j}+u_{2j}=1$.

  接下来，我们希望点 $j$ 到 $c_1$ 的距离越小越好，到 $c_2$ 的距离越大越好。所以与 K-means 类似，我们需要先算距离。
    

  那么，我们给两段距离分别称上相应的几率值。

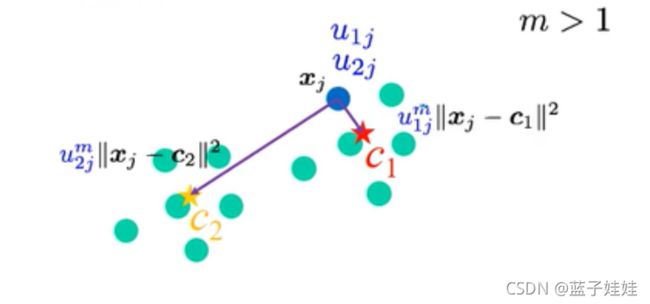
  从图中可以看到，几率值上面多了一个 $m$ ，这个 $m$ 就是 Fuzzifier $m$，用来控制每一段距离重要性的大小，如图上所示，$u_{1j}$ 应该比较大，比如 0.8，$u_{2j}$ 比较小，如 0.2。

  如果 $u_{2j}^m\Vert x_j-c_2\Vert \approx 0$，那么就会忽略 $x_j$ 到 $c_2$ 的距离，只会算 $u_{1j}^m\Vert x_j-c_1\Vert$ 。

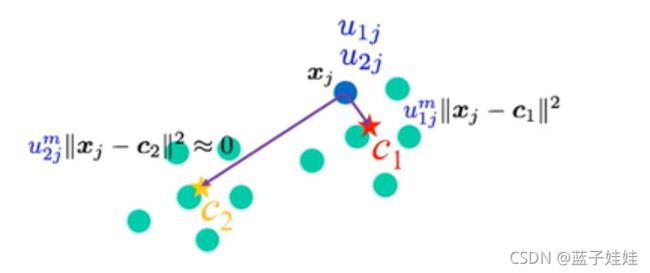
  那么扩展到每一个点，就会得到如下式子：
$$\sum _{j=1}^N{u}_{1j}^m\Vert x_j-c_1{\Vert }^2=u_{1,1}^m\Vert x_1-c_1{\Vert }^2+u_{1,2}^m\Vert x_2-c_1{\Vert }^2+\cdots +u_{1,N}^m\Vert x_N-c_1{\Vert }^2$$
        
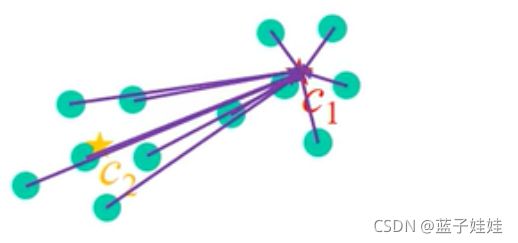
  当我们将 membership values 考虑在内时，到 $c_2$ 的 membership values 会很小，最后乘上距离会场趋近于 0，所以，最后问题近似简化成了只考虑红色区块而已，我们希望距离和越小越好。
      

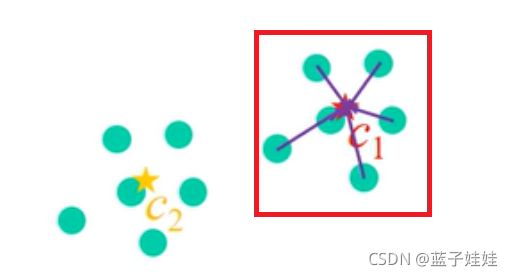
  以此类推，得到：

$$\sum _{j=1}^N{u}_{2j}^m\Vert x_j-c_2{\Vert }^2=u_{2,1}^m\Vert x_1-c_2{\Vert }^2+u_{2,2}^m\Vert x_2-c_2{\Vert }^2+\cdots +u_{2,N}^m\Vert x_N-c_2{\Vert }^2$$

  同样也希望距离和越小越好，那么该栗子的损失函数就是希望 ${\sum }_{j=1}^N{u}_{1j}^m\Vert x_j-c_1{\Vert }^2$ 和 ${\sum }_{j=1}^N{u}_{2j}^m\Vert x_j-c_2{\Vert }^2$ 越小越好，合为一个式子得到：
$$J=\sum _{i=1}^2\sum _{j=1}^N{u}_{ij}^m\Vert x_j-c_i{\Vert }^2=\sum _{j=1}^N{u}_{1j}^m\Vert x_j-c_1{\Vert }^2+\sum _{j=1}^N{u}_{2j}^m\Vert x_j-c_2{\Vert }^2$$

  其中，$c$ 和 $u$ 是未知的。并且满足如下式子：
$$\begin{gathered} \sum _{i=1}^2{u}_{i1}=u_{1,1}+u_{2,1}=1 \\ \dots \\ \sum _{i=1}^2{u}_{iN}=u_{1,N}+u_{2,N}=1 \end{gathered}$$

  将损失函数推广到一般情况为：
$$J(u_{ij},c_i)=\sum _{i=1}^K\sum {j=1}^N{u}_{ij}^m\Vert x_j-c_i{\Vert }^2$$
  其中，${\sum }_{i=1}^K{u}_{ij}=1,j=1,2,\dots ,N$

  举个例子，假设我们有如下4个点，需要将其分为两类。
    
  我们根据距离可能会将 $x_1,x_2$ 分为一类，$x_3,x_4$ 分为一类。

  假设我们知道了第一类的中心为 $c_1$，第二类中心为 $c_2$。那么我们计算损失为：
  

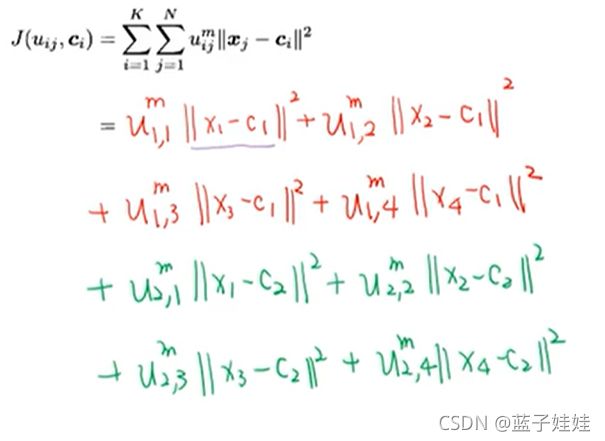
  代入距离为：
  
  如上图如式，当我们已知中心点，那么最后损失函数只与 $u$ 相关，我们希望 $J$ 越小越好。

  反过来，当我们知道了 $U$ 值，那么最后 $J$ 只与 $c$ 相关。
    

  我们的损失函数中的未知量为 $c$ 和 $U$，那么怎么求解以下这种有限制条件的最小值问题，通常的解决方法是使用拉格朗日进行求解。

  我们的每一个限制条件都需要一个拉格朗日因子。如下图所示，对于点 $x_1$，有隶属值 $u_{11}$ 和 $u_{21}$，满足条件 $u_{11}+u_{21}=1$，这里的限制条件用一个拉格朗日因子 ${\lambda }_1$ 表示；同样的对于点 点 $x_2$，有隶属值 $u_{12}$ 和 $u_{22}$，满足条件 $u_{12}+u_{22}=1$，这里的限制条件用一个拉格朗日因子 ${\lambda }_2$ 表示，依此类推，例子中共有10个点，就有10个限制条件，相应的有10个拉格朗日因子。

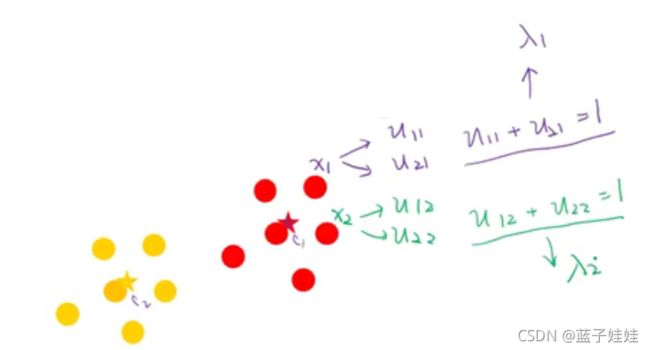
  那么，我们的损失函数变为：
$$\begin{gathered} \mathcal{L}(u_{ij},c_i,{\lambda }_j)=\sum _{i=1}^K\sum _{j=1}^N{u}_{ij}^m\Vert x_j-c_i{\Vert }^2-{\lambda }_1\left(\sum _{i=1}^K{u}_{i1}-1\right)-{\lambda }_2\left(\sum _{i=1}^K{u}_{i2}-1\right)-\cdots -{\lambda }_N\left(\sum _{i=1}^K{u}_{iN}-1\right) \\ =\sum _{i=1}^K\sum _{j=1}^N{u}_{ij}^m\Vert x_j-c_i{\Vert }^2-\sum _{j=1}^N{\lambda }_j\left(\sum _{i=1}^K{u}_{ij}-1\right) \end{gathered}$$

  其中 ${\sum }_{i=1}^K{u}_{i1}-1$ 是限制条件 ${\sum }_{i=1}^K{u}_{i1}=1$ 移项所得。

  我们将 $\mathcal{L}$ 第一部分展开，可得：

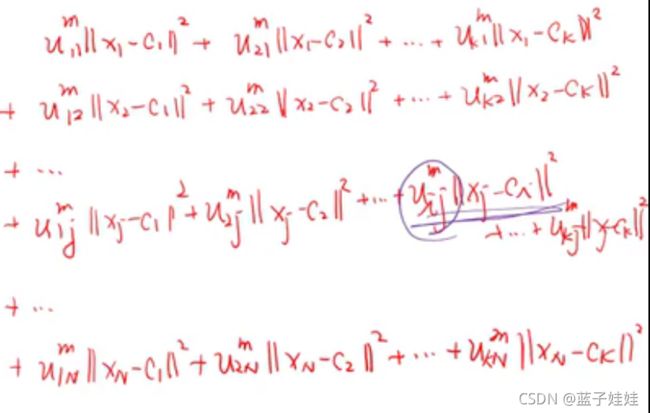
  现在我们要求 $\mathcal{L}$ 对 $u_{ij}$ 的微分，根据上图展开式发现只有一项包含 $u_{ij}$，其余微分时均可看作常量。对于第二项，可以使用相同的方法展开，可得：
    

  那么
$$\begin{gathered} \frac{\partial \mathcal{L}}{\partial u_{ij}}=m{u}_{ij}^{m-1}\Vert x_j-c_i{\Vert }^2-{\lambda }_j=0 \\ =>u_{ij}^{m-1}=\frac{{\lambda }_j}{m\Vert x_j-c_i{\Vert }^2} \\ =\left(\frac{{\lambda }_j}{m}\right)\frac{1}{\Vert x_j-c_i{\Vert }^2} \\ =>u_{ij}={\left(\frac{{\lambda }_j}{m}\right)}^{\frac{1}{m-1}}\frac{1}{\Vert x_j-c_i{\Vert }^{\frac{2}{m-1}}} \end{gathered}$$

  但是，式子中仍有 ${\lambda }_j$ 是未知的，但是我们还有一个限制条件 ${\sum }_{i=1}^K{u}_{ij}=1$.

  将其代入可以得：
$$\begin{gathered} \sum _{i=1}^K{u}_{ij}=\sum _{i=1}^K{\left(\frac{{\lambda }_j}{m}\right)}^{\frac{1}{m-1}}\frac{1}{\Vert x_j-c_i{\Vert }^{\frac{2}{m-1}}} \\ ={\left(\frac{{\lambda }_j}{m}\right)}^{\frac{1}{m-1}}\sum _{i=1}^K\frac{1}{\Vert x_j-c_i{\Vert }^{\frac{2}{m-1}}}=1 \\ =>{\left(\frac{{\lambda }_j}{m}\right)}^{\frac{1}{m-1}}=\frac{1}{{\sum }_{l=1}^K\frac{1}{\Vert x_j-c_l{\Vert }^{\frac{2}{m-1}}}} \end{gathered}$$

  将得到的 $ (\frac{\lambda_j}{m})^{\frac{1}{m-1}} $ 代入 $u_{ij}$ 可得：
$$\begin{gathered} u_{ij}=\frac{1}{{\sum }_{l=1}^K\frac{1}{\Vert x_j-c_l{\Vert }^{\frac{2}{m-1}}}}\cdot \frac{1}{\Vert x_j-c_i{\Vert }^{\frac{2}{m-1}}} \\ =\frac{\frac{1}{\Vert x_j-c_i{\Vert }^{\frac{2}{m-1}}}}{{\sum }_{l=1}^K\frac{1}{\Vert x_j-c_l{\Vert }^{\frac{2}{m-1}}}} \end{gathered}$$

  现在还是以最开始的栗子为例，现有一点 $x_j$ 到 $c_1$ 的距离为 $\Vert x_j-c_1{\Vert }^2$，到 $c_2$ 的距离为 $\Vert x_j-c_2{\Vert }^2$， $x_j$ 应该属于距离近的一类。
      
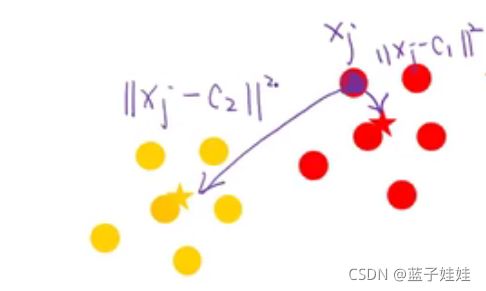
  那么怎么表示距离近呢？我们把距离取倒数，距离越近，倒数就越大。
        
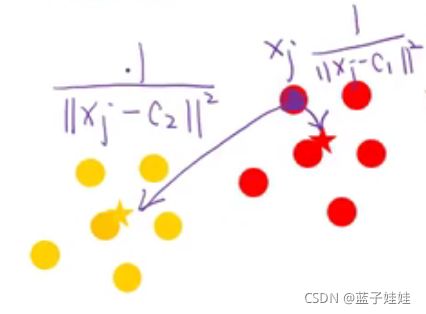
  要满足 $u_{1j}+u_{2j}=1$，类似于数据归一化。我们可以得到：
$$\begin{gathered} u_{1j}=\frac{\frac{1}{\Vert x_j-c_1{\Vert }^2}}{\frac{1}{\Vert x_j-c_1{\Vert }^2}+\frac{1}{\Vert x_j-c_2{\Vert }^2}} \\ {u}_{2j}=\frac{\frac{1}{\Vert x_j-c_2{\Vert }^2}}{\frac{1}{\Vert x_j-c_1{\Vert }^2}+\frac{1}{\Vert x_j-c_2{\Vert }^2}} \end{gathered}$$

  以上就是 $\mathcal{L}$ 对 $u_{ij}$ 微分的推导过程。那么 $\mathcal{L}$ 对 $c_i$ 微分类似。
$$\begin{gathered} \frac{\partial \mathcal{L}}{\partial c_i}=\sum _{j=1}^N{u}_{ij}^m\cdot 2\cdot (x_j-c_i)\cdot (-1) \\ =\sum _{j=1}^N(-2)\cdot u_{ij}^m(x_j-c_i)=0 \\ =>\sum _{j=1}^N{u}_{ij}^m{x}_j-\left(\sum _{j=1}^N{u}_{ij}^m\right)c_i=0 \\ =>c_i=\frac{{\sum }_{j=1}^N{u}_{ij}^m{x}_j}{{\sum }_{j=1}^N{u}_{ij}^m} \end{gathered}$$

那么该算法的流程大致如下;

1. Initialize the membership values $u_{ij}$.
2. At $t$-step: calculate the centers by
   $$c_i=\frac{{\sum }_{j=1}^N{u}_{ij}^m{x}_j}{{\sum }_{j=1}^N{u}_{ij}^m}$$
3. Update $u_{ij}$ by
   $$u_{ij}=\frac{\frac{1}{\Vert x_j-c_i{\Vert }^{\frac{2}{m-1}}}}{{\sum }_{l=1}^K\frac{1}{\Vert x_j-c_l{\Vert }^{\frac{2}{m-1}}}}$$
4. Compute the value of the objective function $J^{(t)}$,
   $$J^{(t)}=\sum _{i=1}^K\sum _{j=1}^N{u}_{ij}^m\Vert x_j-c_i{\Vert }^2$$
5. If $|J^{(t)}-J^{(t-1)}|<ϵ$, then stop; otherwise return to step 2.