python实现Ford-Fulkerson算法--最大流问题

引言

1962 年L.R.Ford和D.R.Fulkerson把原始-对偶算法应用于最大流问题，提出最大流问题的标号算法。简称FF算法。

目录

引言

问题描述

最大流问题

算法思想

操作步骤

标号算法

实现过程

代码实现

python实现如下

---

问题描述

最大流问题

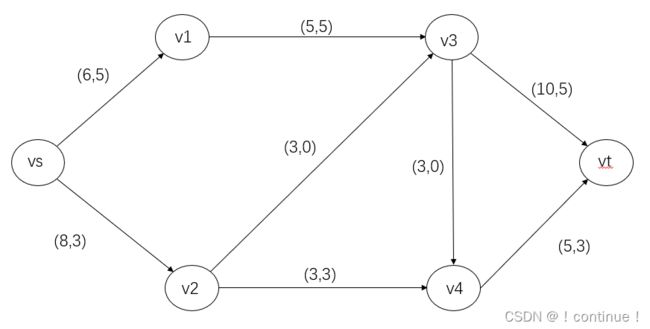
最大流问题（maximum flow problem）属于网络流问题中的一种，是一个组合最优化问题，目的是利用传输工具实现最好的运输流量效果。

算法思想

 从任意一个可行流出发寻找—条增广路径，并在这条增广路径上增加流量，于是便得到一个新的可行流，然后在这新的可行流的基础上再找一条新的增广路径，再增加流量……，继续这个过程，一直到找不到新的增广路径为止。

操作步骤

标号算法

设已有一个可行流f，标号的方法可分为两步：第1步是标号过程，通过标号来寻找可增广链；第2步是调整过程，沿可增广链调整f以增加流量。

1、标号过程

（1）给发点以标号。

（2）选择一个以标记的顶点，对于的所以未给标记的邻接点按下列规则处理：

一、若边，且，则令，并给以标记。

二、若边,且时，令，并给以标号。

（3）重复（2）直到收点被标号或不再有点可标号时为止。

若得到标号，说明存在一条可增广链，转（第2步）调整过程。若未得到标号，标号过程已无法进行时，说明f已为最大流。

2、调整过程

（1）令 

 （2）去掉所以标号，回到第1步，对可行流重新标号

实现过程

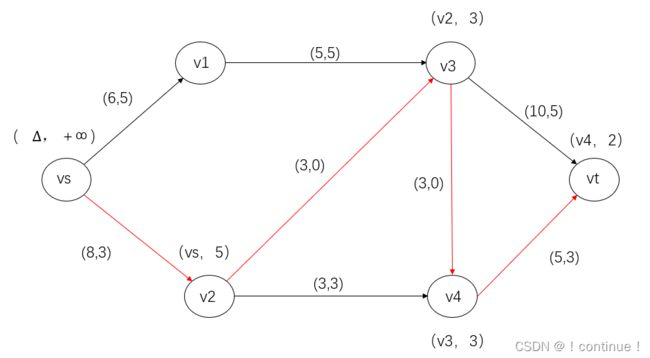
（1）找增广链并给增广链上的点进行标号。

（2）使用标号的最小值，调整增广链上前向边和后向边的流量。

 

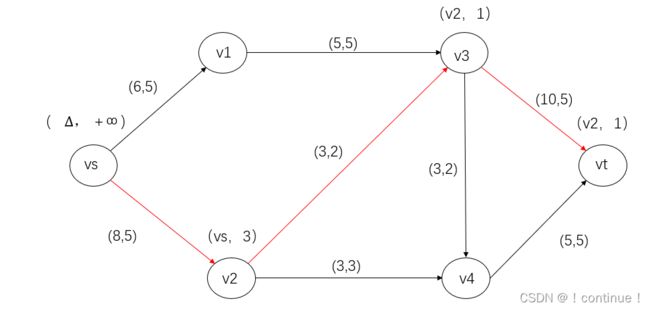
（3）找增广链并给增广链上的点进行标号。

 （4）使用标号的最小值，调整增广链上前向边和后向边的流量。

 

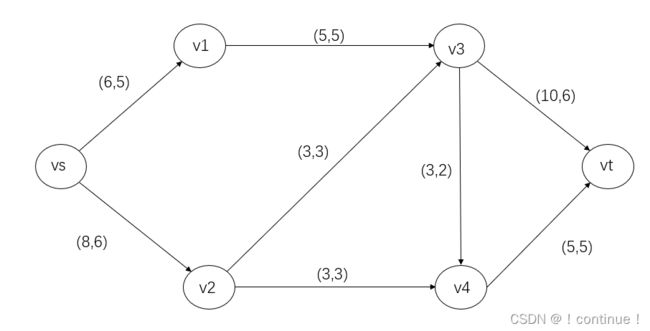
 无法再找到增广链，所以说明f已为最大流。

最大流为：f = 5 + 6 = 11。

代码实现

python实现如下

#深度优先搜索实现Ford-Fulkerson思想
class Graph:
    def __init__(self,num):
        self.data_li = [['inf' for i in range(num)] for i in range(num)]
        self.val_li = [['inf' for i in range(num)] for i in range(num)]

    def add_edge(self,data_r,data_f):  #记录各点到可到达的其余点的路径长度
        for i in data_r:
            self.data_li[i[0]][i[1]] = i[2]
        for i in data_f:
            self.val_li[i[0]][i[1]] = i[2]

    def ford_fulkerson(self,start):
        que = []
        ready = []
        que.append((start,start))
        f_node = (start,start)
        while que:
            curnode = que[-1]
            if curnode[1] == 5:
                val_min = min([self.data_li[j[0]][j[1]] - self.val_li[j[0]][j[1]] if self.data_li[j[0]][j[1]] > 0 else self.val_li[j[0]][j[1]] for j in que[1:]])
                for i in que[1:]:
                    if self.data_li[i[0]][i[1]] > 0:
                        self.val_li[i[0]][i[1]] = self.val_li[i[0]][i[1]] + val_min
                        self.val_li[i[1]][i[0]] = self.val_li[i[1]][i[0]] + val_min
                    else:
                        self.val_li[i[0]][i[1]] = self.val_li[i[0]][i[1]] - val_min
                        self.val_li[i[1]][i[0]] = self.val_li[i[1]][i[0]] - val_min
                que = [que[0]]
                ready = []
                continue
            for i in range(len(self.data_li[curnode[1]])):
                if self.data_li[curnode[1]][i] == 'inf':
                    continue
                else:
                    if self.data_li[curnode[1]][i] > 0:
                        if  self.val_li[curnode[1]][i] < self.data_li[curnode[1]][i] and i != f_node[1] and i != curnode[0] and i not in ready:
                            que.append((curnode[1],i))
                            ready.append(i)
                            break
                    else:
                        if self.val_li[curnode[1]][i] <= abs(self.data_li[curnode[1]][i]) and self.val_li[curnode[1]][i] != 0 and i != f_node[1] and i != curnode[0] and i not in ready:
                            que.append((curnode[1],i))
                            ready.append(i)
                            break
            else:
                f_node = que.pop(-1)
        return self.val_li
if __name__ == '__main__':
    data_r = [(0,1,6),(0,2,8),(1,0,-6),(1,3,5),(2,0,-8),(2,3,3),(2,4,3),(3,1,-5),(3,2,-3),(3,4,3),(3,5,10),(4,2,-3),(4,3,-3),(4,5,5),(5,3,-10),(5,4,-5)]
    data_f = [(0,1,5),(0,2,3),(1,0,5),(1,3,5),(2,0,3),(2,3,0),(2,4,3),(3,1,5),(3,2,0),(3,4,0),(3,5,5),(4,2,3),(4,3,0),(4,5,3),(5,3,5),(5,4,3)]
    d = Graph(6)
    d.add_edge(data_r,data_f)
    path = 0
    for i in d.ford_fulkerson(0)[0]:
        if i != 'inf':
            path = path + i
    print(path)