对数据库几个范式的理解

数据库关系理论

这部分主要是几个概念很抽象，大家开始学可能学不明白。最近在准备复试，复习了一下相关的内容，顺便做一下总结。

先说几个名词：

• 候选码：能够唯一确定一个元组的属性集合称为候选码。注意是集合，所以可能一个候选码可能包含多个元素！一个关系表可能有多个候选码！
• 主码：从候选码中选一个就是主码。
• 主属性：构成候选码的元素之一。

一、函数依赖定义

这里的函数依赖就是X→Y，表示对于任意元组u、v，当u[X] = v[X]时，必有u[Y]=v[Y]。其实和高中的函数定义差不多：一个X总能唯一确定一个Y。这里可以把X看成自变量，Y看成因变量。

平凡函数依赖：当X中包含了Y，还有X→Y，就成他俩是平凡函数依赖。意思就是这种函数依赖很普通，没有什么特殊意义，很平凡。

非平凡函数依赖：当X中不包含Y，还有X→Y。我们基本研究的是非平凡函数依赖。

二、三种函数依赖

1.完全函数依赖：如果X→Y ，并且对于X中的任何一个真子集X’都有Y不函数依赖于X’ ，则称Y对X完全函数依赖。意思就是X可能不止一个元素例如是(Sno,Cno)。那么只有Sno和Cno同时确定，才能确定Y，而单独的Sno和Cno不能够确定Y。

2.部分函数依赖：若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖。其实就是完全函数依赖的对立。X的子集也能决定Y，那就是部分函数依赖。

3.传递函数依赖：如果X→Y ，X不函数依赖于Y， Y→Z且Y不包含于X，Z不包含于Y，则称Z对X传递函数依赖。不用纠结于定义，只要记住X→Y，Y→Z，则有X→Z。

三、四种范式

第一范式1NF

很好记忆，只需要把每个属性值分解成不可再分的元素即可。

第二范式2NF

定义为：一个关系属于1NF，且每个非主属性完全函数依赖于关键字。

也就是说，目标是关键字的子集是不能决定每个非主属性的，而现在有些关键字的子集也能够决定一些非主属性，这就要求我们把关键字拆分。这也意味着我们会从一张表变成多张表。

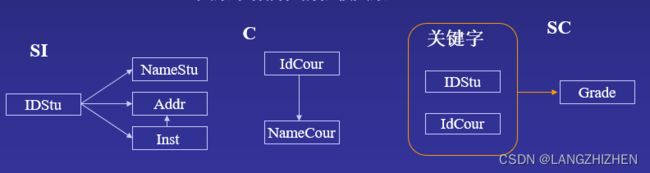
例如

这张图中关键字为（IDStu,IdCour）。（IDStu,IdCour）能够决定NameStu，而子集IDStu也能够决定NameStu，这就不符合完全函数依赖了吧。同理子集IdCour也可以决定非主属性。所以我们需要将一些主属性拆分出来，单独当关键字。

第三范式3NF

定义为：如果关系中每个非主属性不部分依赖于关键字，也不传递依赖于关键字的关系是属于3NF。

其实在2NF的基础上，前半句一定是满足的。我们只需要解决后半句：消除非主属性对关键字的传递依赖。也就是说，不存在X→Y→Z的。会产生传递依赖的原因就是：非主属性之间也产生了函数依赖。所以我们需要把非主属性的函数依赖分解。

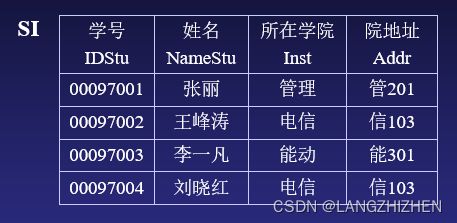
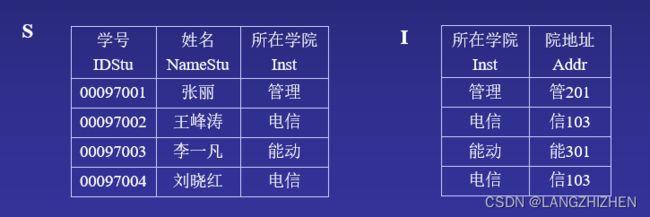
这里IDStu决定了Inst，而Inst又决定了Addr，那么我们需要将这两个函数依赖拆成两张表。

BCNF

定义为：若每一个决定因素都包含码，则称关系属于BCNF范式。

决定因素是指，若这个关系中存在多个函数依赖X→Y，那么每个函数依赖的X就是决定因素。也就是说，BCNF要求关系中所有函数依赖的X都得是码。

这里码有（S，J）和（S，T），决定因素有（S，J），（S，T）和T。因为T不是码，所以不符合BCNF。因此我们需要将T变成码，即把表拆分。

这里码变成了（S，T），T。满足了BCNF范式。

四、总结

光从定义来看比较晦涩难懂，最好是能形象化一点，用自己的理解方式去记忆。

五、补充求闭包

本质上是一个迭代过程，而且也不是很难。做几道题就熟悉了。之前有些数据依赖的公理系统，我感觉太抽象了。看看就好，看不懂不妨碍做题。

核心就是比对$X^i和X^{i+1}$是否相等。而$X^{i+1}$是由$X^i$通过逻辑蕴含得到的，也就是那个→。