二.几何基础_直线

O以下皆为公理推导的定理,有公理组成的新的定义

一.角

1.由线所组成的新的定义

角: 一点出发由两个不同方向的射线组成的图像(注:构成角的边是无界线的)

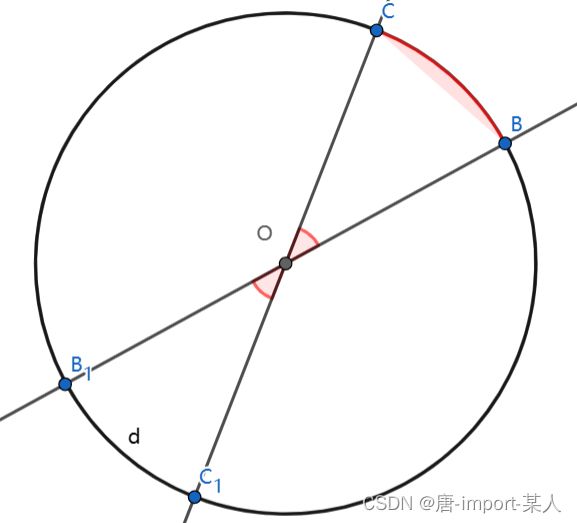
• 顶点: 两射线交汇处,如图 可称顶点为$\angle A或\angle CAB,\angle BAC$
• 边: 构成角的射线,如图 AC确定的射线,和AB确定的射线

2.角衍生定理

全等角: 将一角放置另一角能完全重合,例如∠CAD和∠BAD

• 邻角 有公共顶点,有一条公共边,并且在公共边俩侧的构成的两个角例如∠CAD和∠BAD
  • 公共边: 如图AD所构成的射线
• 角平分线: 将角分割为相等的平分线,例如线AD

倍角: 一个角等于n个相同大小已知角组成的角,则称为角和已知角的关系是n倍角的关系
对顶角: 组成角的射线经顶点延长后形成的射线所组成的角，例如$\angle BAC和\angle B_{1}A{C}_1$

3.角与圆弧的对应

圆心角: 组成角的顶点变为圆心,角的边于圆周相交仅1点。

• 相等圆弧所对的圆心角相同
  • 推导: 构成角的射线与圆心组成的弧角圆周于同一点$B\in OB,C\in OC,于B和C形成\angle BOC,弧CB若同半径的弧相等组成的圆心角也相等$
• 同圆上的弧的大小之比等于圆心角之比
  • 推导: 基于定理相等圆弧所对的圆心角相同可推
• 相等圆弧之和所对应的角度之和相等
  • 推导: 基于定理相等圆弧所对的圆心角相同可推

二.垂直线

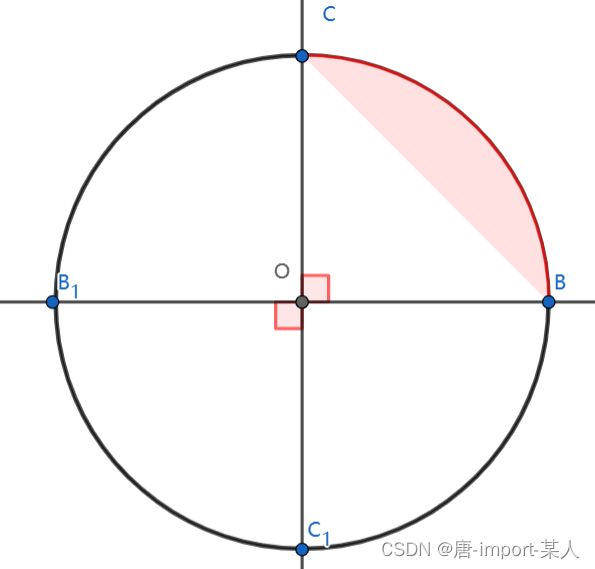
垂直线: 两直线交点o所组成的角的邻角相等。如图所示线$C{C}_1\perp B{B}_1$(ps:在角以知定理情况下的特殊定义)

• 垂直线与圆所组成圆弧为圆周的$\frac{1}{4}$
• $\frac{1}{4}$圆弧所对的角为直角
• 过圆心以若干直线,所组成的弧的和是圆周,对应角的和是4个直角和

三.度量

锐角: 小于直角的角
钝角: 大于直角的角
余角: 两角和为直角
补角: 两角和为2倍直角
度量数: 一个量对选定作为单位的同类量的比,用画图的知识来说就是尺度和单位。（ps:单位是可以设置定义的,同量不同单位之间可以换算单位,即单位的比值)

• 比: 同种类两量之比,a比b就是$\frac{a}{b}$
• 度量数: $\frac{量}{单位量}$
• 同度量数之比等于商之比: $\frac{量1}{单位量}:\frac{量2}{单位量}=\frac{量1}{量2}$

1.度

①360=1圆周
习惯上分圆周为360份,每份称为度。1度=60分=3600秒,度的符号用°来表示。

• 直角的度是$\frac{360°}{4}=90°$

②400=1圆周
可以分圆周为400份(事实上你可以划分为任何份),那么直角就是100

四.定理

①过直线外一点只可引一条与该线垂直的线

• 推导: 两个线所形成的角只有一个位置会是直角。而这个位置上的线就是垂线

②对称点: 直线上有两点关于一点的距离相等,则两点为对称点

• 推导: 射线上有一点$O$,绕射线起点旋转180°,此时射线上的点为$O^1$。则点O与$O^1$是对称点,二者距离射线起点的距离相同

五.例题

1.设M为线段AB的中点,证明①若点C在线段AB上,CM的距离是CA和CB的差的一半②若点C在线段的延迟线外,CM的距离是CA和CB之和的一半

• ①证明若点C在线段AB上,CM的距离是CA和CB的差的一半:
  

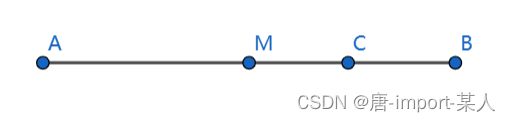
  假设C点在M与B的线段上
  $\because M为AB中点,点C在AB线段上$
  $\therefore AM=MB=L,CM=l,AC+CB=AB=2L$
  $\therefore AC=L+l,CB=L-l$
  $\therefore CM=\frac{AC-CB}{2}$
  $\because 由于对称点的定理看推导C在线段AM上时结论一致$
  $\therefore CM=\frac{AC-CB}{2}$

• ②证明若点C在线段的延迟线外,CM的距离是CA和CB之和的一半:
  

  假设延迟线是沿着MB的
  $\because M为AB中点$
  $\therefore AM=MB=L,CB=l,AB=2L$
  $\therefore AC+BC=AB+BC+BC=2L+2l$
  $\because CM=MB+BC=L+l$
  $\because CM=\frac{AC+BC}{2}$

2.设OM为∠AOB的平分线,证明①若射线OC在∠AOB内,则∠COM=∠COA与∠COB之差的一半。②若射线OC在∠AOB的对顶角$\angle A^{1}O{B}^1$内,则∠COM等于前两个角差一半的补角③若射线OC在两条直线形成的$\angle BO{A}^1或\angle AO{M}^1$内部,则$\angle COM$等于∠COA,∠COB之和的一半

• ①证明若射线OC在∠AOB内,则∠COM=∠COA与∠COB之差的一半:
  

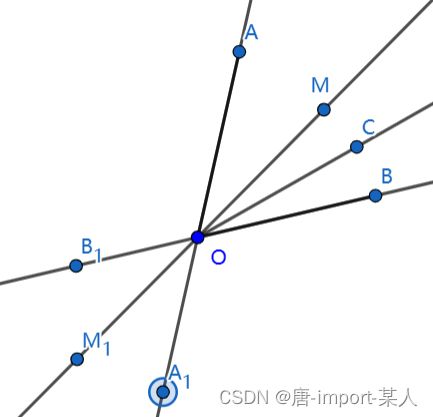
  先假设OC在MOB内
  $\because OM为\angle AOB的平分线$
  $\therefore \angle AOM=\angle BOM=\angle 1$
  $\because OC在\angle AOB内$
  $\therefore \angle AOC+\angle COB=\angle AOB=2\angle 1$
  $\therefore \angle COA-\angle COB$
  $=\angle 1+\angle COM-(\angle 1-\angle COM)$
  $=2\angle COM$
  $\therefore \angle COA-\angle COB=2\angle COM$
  根据对称原理可推导OC在∠AOM内的结果一致

  • 奇思妙想: 值得注意的是这里面的推导的结果和题目1里面的①类似。倍数关系是一致的。所以可以把该角的问题转换为曲线AMCB上,或者是AMCB投影到一条线段上即题目1里面的①

• ②证明若射线OC在∠AOB的对顶角$\angle A^{1}O{B}^1$内,则∠COM等于前两个角差一半的补角:
  

  假设OC在$\angle B_{1}O{M}_1$中
  $\because 根据对顶角原理做延长的边O{B}_1.O{M}_1,O{A}_1,O{C}_1$
  $\therefore \angle CO{M}_1=\angle C_{1}OM$
  $\because ①中所推$
  $\therefore \angle COA-\angle COB=2\angle C_{1}OM$
  $\because \angle COM$
  $=\angle CO{C}_1-\angle C_{1}OM$
  $=180°-(\angle COA-\angle COB)$
  $\therefore \angle COM=180°-(\angle COA-\angle COB)$
  根据对称原理可推导OC在$\angle A_{1}O{M}_1$内的结果一致

  • 奇思妙想: 这里面要巧用对顶角对应延长边为平角,当遇到复制问题时,可以根据对称原理先解决简单问题,再返回处理复制问题

• ③若射线OC在两条直线形成的$\angle BO{A}^1或\angle AO{M}^1$内部,则$\angle COM$等于∠COA,∠COB之和的一半
  

  假设OC在$\angle BO{A}^1$中
  $\because OM为\angle AOB的平分线$
  $\therefore \angle AOM=\angle BOM=\angle 1$
  $设\angle COB=\angle 2$
  $\therefore \angle COA=2\angle 1+\angle 2$
  $\because \angle COM=\angle AOM+\angle BOM+\angle BOC$
  $=\angle 1+\angle 2$
  $=\frac{\angle COA+\angle COB}{2}$
  $=\frac{2\angle 1+2\angle 2}{2}$
  $\therefore \angle COM=\frac{\angle COA+\angle COB}{2}$
  根据对称原理可推导OC在$\angle AO{M}^1$内的结果一致

  • 奇思妙想: 值得注意的是这里面的推导的结果和题目1里面的②类似,其倍数关系是一致的。所以可以把该角的问题转换为曲线AMBC上,或者是AMBC投影到一条线段上即题目1里面的②

3.从点O依次引四条半直线,OA,OB,OC,OD,且∠AOB=∠COD,∠BOC=∠DOA,证明OA和OC互为延长线,OB和OD也是一样

$\because \angle AOB+\angle BOC=\angle AOC,\angle COD+\angle DOA=\angle COA$
$\therefore \angle AOB+\angle BOC=\angle COD+\angle DOA$
$\because \angle AOB+\angle BOC+\angle COD+\angle DOA=2\pi$
$\therefore \angle AOB+\angle BOC=\angle COD+\angle DOA=\pi$
所以可知点A点C在同一条直线上
同理$\angle DOA+\angle AOB=\angle BOC+\angle COD$=>点B,D在同一条直线上

4.设OA,OB,OC,OD是依次顺序的半直线,满足条件∠AOB和∠COD的平分线形成一条直线。∠BOC和∠AOD平分线形成一条直线。证明四条半直线互为延长线

$设\angle AOB的平分线为OM,\angle COD的平分线为O{M}^1,\angle BOC的平分线为ON,\angle AOD的角平分线为O{N}^1$
$\because M{M}^1,N{N}^1为一条直线$
$\therefore \{\begin{array}{l}\angle AOM=\angle MOB=\frac{\angle AOB}{2}\\ \angle CO{M}^1=\angle M^{1}OD=\pi -\angle COM=\pi -\angle MOD=\frac{\angle COD}{2}\\ \angle BON=\angle NOC=\frac{\angle BOC}{2}\\ \angle AO{N}^1=\angle N^{1}OD=\pi -\angle AO{N}^1=\pi -\angle N^{1}OD=6\frac{\angle AOD}{2}\end{array}$
$\because \{\begin{array}{l}\angle AOM+\angle CO{M}^1=\angle MOB+\angle M^{1}OD\\ \angle AOM+\angle M^{1}OD=\angle MOB+\angle CO{M}^1\\ \angle BON+\angle AO{N}^1=\angle BON+\angle N^{1}OD\\ \angle BON+\angle N^{1}OD=\angle BON+\angle AO{N}^1\end{array}$
$\because \{\begin{array}{l}\angle AOM+\angle COM=\angle MOB+\angle MOD\\ \angle AOM+\angle MOD=\angle MOB+\angle COM\\ \angle BON+\angle AON=\angle BON+\angle NOD\\ \angle BON+\angle NOD=\angle BON+\angle AON\end{array}$
$\because \{\begin{array}{l}\angle AOC=\angle BOD\\ \angle AOD=\angle COB\\ \angle AOB=\angle BOD\\ \angle BOD=\angle AOB\end{array}$
$\therefore \angle AOB=\angle AOC=\angle BOD=\angle AOD$
$\because \angle AOB+\angle AOC+\angle BOD+\angle AOD=2\pi$
$\therefore \angle AOB=\angle AOC=\angle BOD=\angle AOD=\frac{\pi }{2}$
故四条半直线互为延长线