《离散数学》第一章:集合论
1.2集合
集合是不能被精确定义的的基本数学概念。通常,集合是由指定范围内的满足给定条件的所有对象聚集在一起构成的。
指定范围内的每一个对象称为这个集合的元素。
1.2.1集合的表示
集合是由它所包含的元素完全确定的。为了表示一个集合,可以有许多方法。
1.枚举法(显示法)
列出集合中全部元素或部分元素且能看出其他元素规律的方法焦耳枚举法(显示法)。一般来说,当一个集合仅含有限个元素或元素之间有明显关系时,通常采用枚举法(显示法)。
枚举法实际上是一种显示表示法,其优点在于具有直观性。但是,对某些集合,列出所有元素是不可能的。而且,从计算机的角度看,显示法是一种“静态”表示法,如果同时将所有的“数据”都输入到计算机中,则会占据大量的“内存”,为此,给出另一种描述集合的方法——叙述法(隐式法)。
2.叙述法(隐式法)
通过刻画集合中元素所具备的某种特性来表示集合的方法称为叙述法(隐式法),通常用符号P(x)来表示不同对象x所具有的性质P,由P(x)所定义的集合尝记为{x|P(x)}
例如:Z={x|x是一个整数};
叙述法(隐式法)的特点在于表示集合的元素可以是很多个或无穷个,而且从计算机的角度看,叙述法(隐式法)是一种“动态”的表示法,计算机在处理数据时不用占据大量“内存”。
3.归纳法
归纳法时指通过归纳定义集合的方法,主要由以下三部分组成。
第一部分:基础,指出某些基本的元素属于某集合。
第二部分:归纳,指出由基本元素构成新元素的方法。
第三部分:极小性,指出该集合的界限。
第一部分和第二部分指出一个集合至少要包含的元素,第三部分指出一个集合至多要包含元素。
例如:集合A按如下方式定义:
(1)0和1都是A中的元素;
(2)如果a,b是A中的元素,则ab,ba也是A中的元素;
(3)有限次使用(1)、(2)后所得到的字符串都是A中的元素。
4.递归指定集合法
递归指定集合法是指通过计算机规则定义集合中的元素的方法。
5.文氏(Venn)图解法
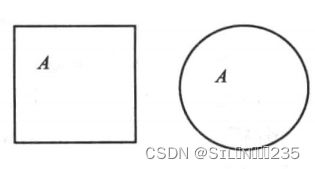
文氏图解法是一种利用平面上点的集合做成对集合的图解的方法。一般用平面上的方形或圆形表示一个集合。
1.2.2集合与元素的关系
元素与集合之间的“属于”关系是“明确”的。对于某个集合A和元素a来说,a或者属于集合A,或者不属于集合A,两者必居其一且仅居其一。这里将语句“a是集合A中的元素”或“a属于A”记为a∈A
而语句“a不属于A中的元素”或“a不属于A”记为a∉A
在离散数学中,仅仅对界限清楚、无二义性的描述进行讨论,而由不清晰的对象构成的集合属于模糊集合论的研究范畴。
1.2.3集合与集合的关系
集合中元素的顺序并不十分重要,另外,在集合中,凡是相同的元素,均可认为是同一元素,并可将相同的元素合并成一个元素。因此,集合中的元素是唯一确定并可加以区分的对象,即集合中的元素是互异且无序的。
假设两个集合中的元素完全相同,称这样的两个集合相等。
定理1:(外延性原理) 两个集合A和B相等,当且仅当它们的元素完全相同,记为A=B,否则,A与B不相等,A≠B。
定义:设A、B是任意两个集合,如果B的每一个元素都是A的元素,则称B是A的子集合,简称子集,这时也称B被A包含,或A包含B,记作B⊆A,A⊇B,称“⊆”或“⊇”为被包含关系或包含关系。如果B不被A所包含,则记作B⫋A。
上述子集定义的数学语言描述为
B⊆Aó对∀x,如果x∈B,则x∈A
有子集的定义不难得出:对任意集合A,都有A⊆A。
定理1.2.2 设A,B是任意两个集合,A⊆B,B⊆AóA=B。
则称B是A的真子集,记作B⊂A,称“⊂”为真包含关系,其文氏图表示为:
如果B不是A的真子集,则记作B⊄A。
上述真子集定义的数学语言描述为:
B⊆Aó对∀x,如果x∈B,则x∈A,并且存在y∈A,但y∉B。
1.2.4几个特殊的集合
定义1.2.3 不含任何元素的集合叫做空集,记作∅,空集可以符号化为
∅={x|x≠x}
空集是客观存在的。
定理1.2.3 (1)空集是一切集合的子集。
(2)空集是绝对唯一的
定义1.2.4 在一个相对固定的范围内,包含此范围内的所有元素的集合,称为全集或论集,用U和E表示,用文氏图表示为:
定理1.2.4 全集是相对唯一的。
定义1.2.5 集合A中的元素个数称为集合的基数,记为|A|。
如果一个集合的基数是有限的,则称该集合为有限集。
如果一个集合的基数是无限的,则称该集合为无限集。
定义1.2.6 如果一个集合A含有n个元素,则称集合A为n元集,称A含有m个(0≤m≤n)元素的子集为它的m元子集(真子集个数)。
一般来说n元集共有2n个不同的子集。
定义1.2.7 设A为任意集合,把A的所有不同子集构成的集合叫做A的幂集,记作P(A)(或2A),其符号化表示为P(A)={x|x⊆A}
事实上,把集合作为元素而构成的集合称为集族,显然,幂集是集族。
1.2.5 集合的运算
定义1.2.8 设U是全集,A,B是U的两个子集,则
- A∪B={x|x∈A或x∈B}仍是一个集合,称A与B的并集,称“∪”为并运算。
- A∩B={x|x∈A且x∈B}仍是一个集合,称A与B的交集,称“∩”为交运算。
- A-B={x|x∈A并且x∉B}仍是一个集合,称A与B的差集,称“-”为差运算。
- A=U-A称为集合A的补集(也可以记为A’,~A),“---”称为补运算;
- A⊕B={x|(x∈A且x∉B)或(x∈B且x∉A)}=(A-B)∪(B-A)仍是一个集合,称它为A与B的对称差集,称“⊕”为对称差运算。
定理1.2.5 设U是相对于A的全集
- A∪A=A;A∩A=A(幂等律)
- A∪B=B∪A;A∩B=B∩A(交换律)
- A∪(B∪C)=(A∪B)∪C;A∩(B∩C)=(A∩B)∩C(结合律)
- A∪∅=A;A∩U=A(同一律)
- A∪U=U;A∩∅=∅(零律)
- A∩(B∪C)=(A∩B)∪(A∩C)
A∪(B∩C)=(A∪B)∩(A∪C)(分配律)
- A∩(A∪B)=A,A∪(A∩B)=A(吸收律)
- A∩A的补集=∅(矛盾律)
- A∪A的补集=U(排中律)
 A的补集的补集=A(否定律)
A的补集的补集=A(否定律)
1.2.6集合的难点
对于集合,需要注意以下几点:
- 在集合的表示方法中,归纳法相对难以理解,在理解归纳法时,一定要注意它是由三个部分组成的,三个部分缺一不可,是一种构造性的集合定义的方法。
- 当以一个集合作为另一个集合的元素考察元素于集合、集合与集合之间的关系时,要从它本身是一个集合与它还是另一个集合的元素这两个方面进行考虑。
- 注意对幂集的理解,它是以元素的集合,集合的幂集是由该集合的所有不同子集构成的集合。
- 集合运算可以看作时实数集合定义上的运算的进一步推广,注意正确理解集合基本运算的定义以及相应的定律。
1.3无限集
1.3.1可数集合和不可数集合
冯诺依曼用集合的方式定义了自然数,其定义是:
- ∅∈N
显然,每一个自然数都对应一个集合.
定义1.3.1 设A、B为两个集合,若在A,B之间存在一一对应关系:
则称A与B是等势的,记作:A~B,也称集合A、B等势。
由定义可知,如果A=B,则A~B,反之不一定成立。
定义1.3.2 凡与自然数N等势的集合,称为可数集合,该集合的基数记作:ℵ0(读作阿列夫零)
定理1.3.1
- 两个有限集合等势当且仅当它们有相同的元素个数;
- 有限集合不和任何真子集等势;
- 可数集合可以与其可数的真子集等势。
定义1.3.3 开区间(0,1)称为不可数集合,其基数记为ℵ(读作阿列夫),凡与开区间(0,1)等势的集合都是不可数集合。
R也是一个不可数集合。
1.3.2无限集的难点
对于无限集,需要注意有限集与无限集的区别和联系,尽管无限集与有限集相比,仅是数量上的改变,但却引起了质的变化。对于无限集数量的度量是通过是否与自然数N和(0,1)开区间存在一一对应关系来衡量的。
1.4集合的应用
集合在计算机中的表示。在计算机中表示集合的方法很多,其中一种就是无序地将集合中的元素存放在计算机里面。但是如果这样存放,那么集合的交、并和差等运算就需要进行元素的搜索,从而产生不必要的时间开销。
一种元素的有序存储方法:假设全集U是有限集合,A={a1,…,an}是U的一个子集且对应长度为n的比特串B=b1b2…bn,其中,如果ai∈A,则bi=1,否则bi=0,这样就可以容易地在计算机中计算集合的交、并、差等运算了。
1.5总结
(1)集合的定义、集合的正确表示、集合基数的正确计算、元素与集合的关系和集合与结集合的关系的判断
(2)正确理解空集的唯一性、全集的相对唯一性;熟记空集是一切集合的子集,任何集合都是它自身的子集。
(3)正确理解有限集与无限集的联系和区别
(4)集合的基本运算的定义和满足相关的运算律,以及相对应的文氏图表示。正确理解各种定义和运算律是正确计算集合各种运算的关键。