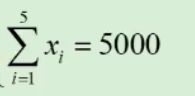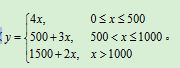数学建模-Lingo学习

数学建模-Lingo学习

注意：

• 放大缩小字体：ctrl+滚轮

• 每行句子一定要加分号，否则会报错。

• lingo的加+减-乘*除 /

• 2*x不能写成2x

• lingo的注释:

   !我是注释;
  

• lingo是不解析空格的

• lingo的语句是没有逻辑先后关系的

• for和sum中可以省略i,但是必须同带或者同不带

• 使用矩阵工厂创建矩阵后,整个程序需要用model:和end套起来

Lingo的变量:

1. Lingo默认所有变量为大于等于0的数字,因此非负的条件不必多写
2. 万一一个变量可以小于0,会有一个函数叫@free,来使定义域为R.
3. a和A等价,Lingo并不区分大小写,aaa和AaA,AAa都被看作一个变量(最好写小写)
4. 变量由字符数字下划线构成,且字母在首位,与Matlab命名相同

入门案例

输入

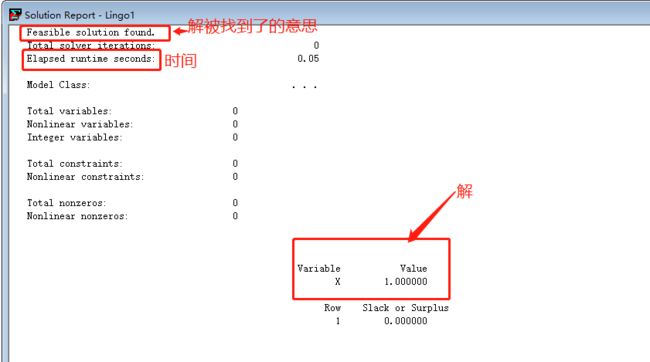
x+1=2;

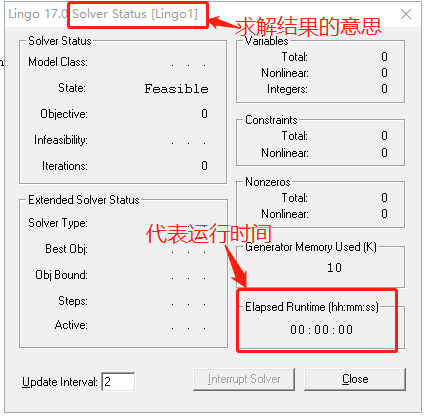
点击运行，返回一个弹框

叉掉后 是一个文本框，内容是可以修改的

用Lingo解方程

题1(两个等式方程组成的方程组)

求解方程组

下面是图示方便理解,后面的案例会直接文字说明

结果

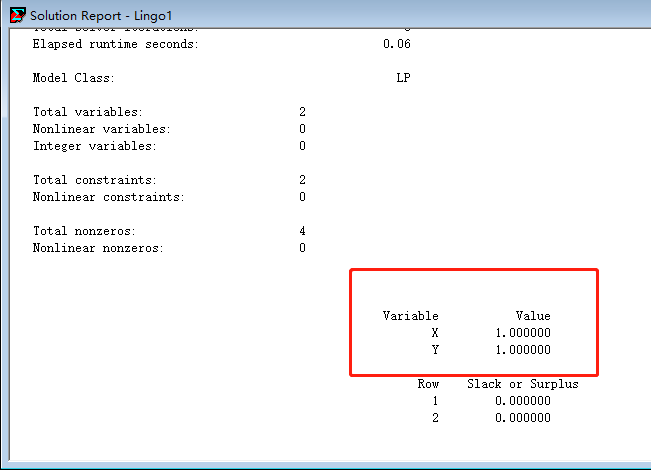
题2(两个等式方程和两个不等式方程组成的方程组)

求解方程组

在Lingo Model中输入

x^2+y^2+2*x=103;
2*x+y=12;
y>5;
!这里并不需要写x>0,因为lingo中默认变量大于0;

然后点击运行按钮

线性规划基础

1. 一个线性规划中只含有一个目标函数.(两个以上的是多目标线性规划,Lingo无法直接解,除非利用模型将两个目标函数整合成一个目标函数)
2. 求目标函数最大值或最小值分别用max=…或min=…来表示
3. 线性规划和非线性规划的本质区别是目标函数是否线性,其余一致,不需要区分.但需要注意,非线性规划的求解非常困难,基本得不到全局最优解

题

在lingo窗口中输入

max = 200*x1 + 300*x2;
x1 <= 100;
x2 <= 120;
x1+2*x2 <= 160;

主要是

集合&矩阵工厂

直接上题 = =

引题

解法1 暴力枚举法

①分解

​ lingo中输入

a1 = 1;
a2 = 2;
a3 = 3;
a4 = 4;
a5 = 5;
max = s;
s = a1*x1;
s = a2*x2;
s = a3*x3;
s = a4*x4;
s = a5*x5;
x1 + x2 + x3 + x4 + x5 = 5000;

结果

由上面我们可以看出暴力解法操作是复杂繁琐的.由此引出矩阵工厂

矩阵工厂:生产一维矩阵

输入

sets:
factory /1..6/ : a,b;   !1行6列的矩阵;
plant /1..3/ : x,y;    !1行3列的矩阵;
endsets

结果

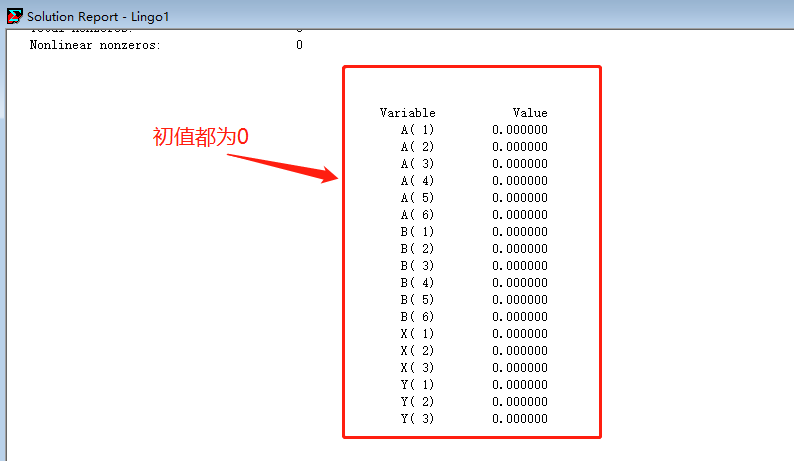
lingo中不分先后,只看你方程例如写一个A(1)=20;A(2)=30;则会报错,因为矛盾了

总结:

• factory和planet都是制造矩阵的工厂,但是两个不同的工厂.
• factory工厂后面的/1…6/说明他专门生产1×6的工厂,上面的a,b都是1×6的矩阵
• planet工厂后面的/1…6/说明他专门生产1×6的工厂,上面的x,y都是1×6的矩阵
• factory和planet都是随便起得, abxy也是随便起的
• 上面的语句本质是定义了4个行矩阵大小,矩阵工厂只是中介
• 生产完矩阵后,工厂和矩阵之间会脱开联系
• Lingo不是一行行读代码的,所以用sets:和endsets表示矩阵工厂生产流程的起止.

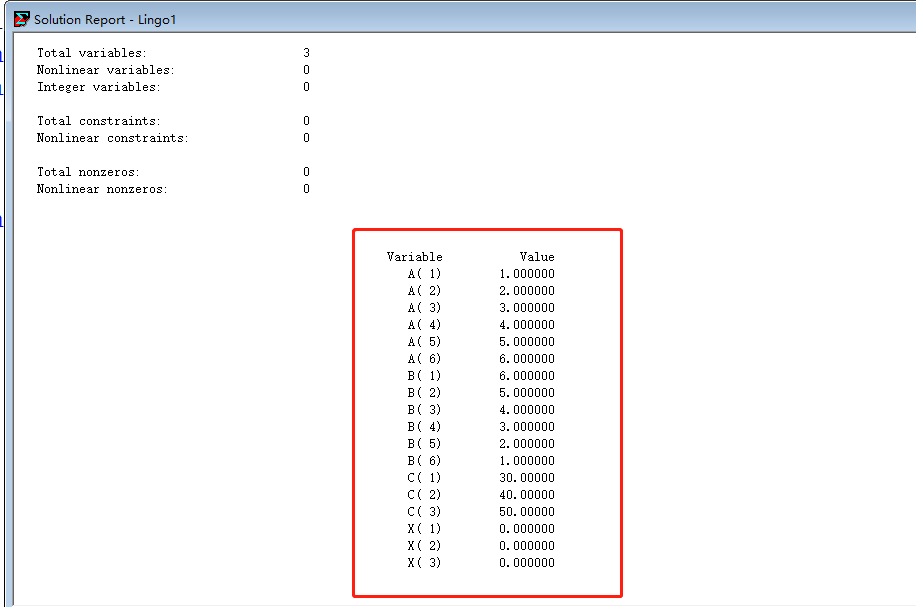
矩阵的赋值

输入

sets:
factory /1..6/: a,b;
plant /1..3/: c,x;
endsets
data:
a = 1,2,3,4,5,6;
b = 6.0,5.0,4.0,3.0,2.0,1.0;
c = 30,40,50;
enddata

注意点:

• 不是每个矩阵都需要赋值,有些矩阵正是我们要求解的变量.
• 需要赋值的矩阵必须赋满,不能给6个元素的矩阵只赋3个数值
• Lingo中可以给矩阵赋整数,也可以赋小数,但不能赋值分数
• Lingo不是一行一行读代码的,可以用data:和enddata表示矩阵赋值的起止,先sets后data赋值

循环与求和

例题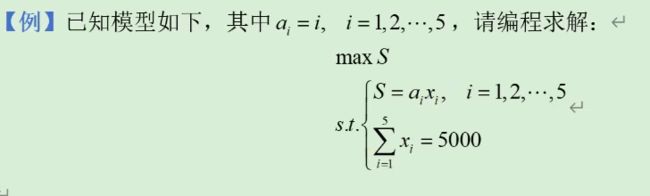

约束条件1 S=aixi, i=1,2,…,5 利用for循环求解

@for(gc(i):S=a(i)*x(i));
!for循环的替代
S = a(1)*x(1);
S = a(2)*x(2);
S = a(3)*x(3);
S = a(4)*x(4);
S = a(5)*x(5);
;

• for循环,括起整行语句,因为S=aixi,i=1,2…,5相当于5个约束条件
• for循环内部先写工厂,也就是gc(i),告诉for循环几次,然后写约束条件,也就是s=ax
• 此处的i可带课不带,也可以换成 j,k…啥的
• 二维矩阵工厂出现后会同时有i和j,那时必须带i和j.

约束条件2用sum求和

@sum(gc(i):x(i))=5000;
!sum的替代
x(1)+x(2)+x(3)+x(4)+x(5)=5000;
;

总程序

model:
sets:
gc /1..5/ : a,x; !创建gc这个工厂;
endsets

data:
a = 1,2,3,4,5;
enddata

max = S;
@for( gc(i) : S = a(i)*x(i) );
@sum(gc(i):x(i))=5000;
end

• sum求和括号内不能放约束条件
• sum求和,先写工厂,告诉要求和几次,然后括号外写约束条件

for和sum的使用情景:

1. 约束条件后面有i=1,2,3…,5 一定在最外层套上for
2. 约束条件前面是一定在中间加上sum.

二维矩阵

模板.不能直接用数字声明几行几列,按模板走

sets:
factory /1..6/: a;
plant /1..3/: b;
Cooperation (factory,plant) : c,x; !6行3列矩阵;
endsets

• Cooperation大工厂是由factory和plant两个小工厂合并的,生产6×3矩阵.
• a是1×6的矩阵,b是1×3的矩阵,c和x都是6×3列的矩阵
• 若调换factory和plant则Cooperation生产3行6列矩阵
• Cooperation不是固定的 都是随便取的

二维工厂的赋值

sets:
factory /1..6/: a;
plant /1..3/: b;
Cooperation (factory,plant) : c,x; !6行3列矩阵;
endsets
data:
c=1,2,3
  3,2,1
  3,4,5
  6,7,8
  9,6,4
  2,3,4;
enddata

结果

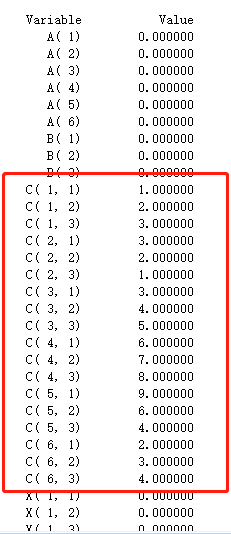
例题

model:

sets:
factory /1..6/ : a;
plant /1..8/ : d;
coo (factory,plant): c,x;
endsets

data:
a = 60,55,51,43,41,52;
d = 35,37,22,32,41,32,43,38;
c =	6,2,6,7,4,2,5,8
	4,9,5,3,8,5,8,2
	5,2,1,9,7,4,3,3
	7,6,7,3,9,2,7,1
	2,3,9,5,7,2,6,5
	5,5,2,2,8,1,4,3;
enddata

!嵌套 更普便适用一些 双for循环的感觉
min = @sum(factory(i) : @sum(plant(j):c(i,j)*x(i,j)));
;
!目标函数;
min = @sum(coo(i,j):c(i,j)*x(i,j));
!约束条件;
@for(factory(i):@sum(plant(j):x(i,j))<=a(i));
@for(plant(j):@sum(factory(i):x(i,j)) = d(j));
!xij大于等于0,可加可不加,因为lingo中默认大于0;
end

运算符

关系运算符

• 关系运算符往往在约束条件中,用来指定约束条件左右两边必须满足的关系
• Lingo中只有三种关系运算符:= >= <=没有单独的> <若出现Lingo默认省略了=,但是在最优化问题中,可以不用管这些,看到大于就大于,看到小于就小于,因为误差极小.

算术运算符

两个数字之间

运算符	翻译理解	作用
#eq#	equal	两边相等为真
#ne#	not equal	两边不等为真
#gt#	greater than	左边大于右边为真
#ge#	greater equal	左边大于等于右边为真
#lt#	less than	左边小于右边为真
#le#	less equal	左边小于等于右边为真

有点像shell编程里面的运算符,只不过那个没有两边的#

逻辑表达式

运算符	翻译理解	作用
#not#	非	单目运算符，表示取反
#and#	与	左右两边均正确才为真
#or#	或	左右两边均错误才为假

逻辑运算符唯二出现的位置：

a) for循环与sum求和。

b) if判断中。

例题

1.若矩阵a=[6,5,4,3,2,1],用集合的语言求解a(4)+a(5)+a(6)

model:

sets:
fac /1..6/ : a;
endsets

data:
a=6,5,4,3,2,1;
enddata

y=@sum(fac(i) | i#ge#4 : a(i));!i大于等于4的a(i)和;

end

2.若矩阵a由六个元素组成,且a(i)>5,i=1,2,5,6. 求矩阵a各元素求和的最小值

model:

sets:
fac /1..6/:a;
endsets

min = @sum(fac(i):a(i));
@for(fac(i) | i#le#2 #or# i#ge#5 : a(i)>5);
!解法2
@for(fac(i) | i#ne#3 #and# i#ne#4 : a(i)>5);
;
end

3.若矩阵 a=1 2 3 求矩阵上三角之和（含主对角线）

​ 4 5 6

​ 7 8 9

model:
sets:
fac / 1..3 / : ;
coo(fac,fac) : a;
endsets
data:
a = 1,2,3
	4,5,6
	7,8,9;
enddata
y=@sum( coo(i,j) | i#le#j : a(i,j) );
end

Lingo内置函数

if判断例题(一般情况下不要用if,多用sum和for)

1.用Lingo表达出分段函数，并求出x为一系列数值时的结果。

@free(x);
@free(y);
x = -10;
! 给x一个随机的初值;
y = @if( x#ge#0 , x+10 , x-10 );

2.用Lingo表达出分段函数

x =1500;
! 给x一个随机的初值;
y = @if( x#le#500 , 4*x , @if( x#gt#1000 , 1500+2*x , 500+3*x ));

变量定界函数

函数	作用
@bin(x)	限制x只能取0或1,0-1规划中特别有用	有病是1,没病就0
@gin(x)	限制x为整数，在整数规划中特别有用
@bnd(a,x,b)	限制a<=x<=b,可以直接替换两个约束条件
@free(x)	取消对变量x非负的限制,让他的定义域为R

@bnd(a,x,b):求函数在y = 2x在(1,3)之间的最大值

@bnd(1,x,3);
max = 2*x;

第一句可写为x>1;x<3;(如果用这个的话.lingo会从所有数中随机进行匹配,用@bnd函数则会规定在区间内找)代替,但是不论从速度还是代码量都不如@bnd函数

0-1整数规划

@bin:已知a = [2,9,3,8,10,6,4,10]以及b=[1, 3, 4, 3, 3,1, 5,10]，求以下线性规划：0-1整数规划

model:

sets:
fac /1..8/: a,b,x ;
endsets

data:
a = 2,9,3,8,10,6,4,10;
b = 1,3,4,3,3,1,5,10;
enddata
max = @sum( fac(i) : a(i)*x(i) );
@sum(fac(i):b(i)*x(i)) <= 15;
@for(fac(i):@bin(x(i))); !最后一个约束条件;

end

整数规划

@gin:已知a=[2.1 1.0 1.8 1.2 2.0 1.2]以及b=[6 125 12500 345 5] 求整数规划:

model:
sets:
factory /1..6/ : a,x;
plant /1..5/ : b;
coo(factory,plant):c;
endsets
data:
a=2.1 1.0 1.8 1.2 2.0 1.2;
b=6 125 12500 345 5;
c=0.45 20 415 22 0.3
0.45 28 4065 5 0.35
0.65 40 850 43 0.6
0.4 25 75 27 0.2
0.5 26 76 48 0.4
0.5 75 235 8 0.6;
enddata
max=@sum( factory : a*x );
@for( plant(j) : @sum(factory(i):c(i,j)*x(i))<=b(j) );
@sum( factory : x )=14;x(2)<=3;x(4)<=2;
@for( factory(i) | i#ne#2 #and# i#ne#4 : @bnd(1,x(i),4)    );
@for( factory : @gin(x) );!最后一个约束条件;
end

数学函数

类别	函数名	返回值
三角函数	@sin(x) @cos(x) @tan(x)	返回x的正弦值 返回x的余弦值 返回x的正切值
指数对数	@log(x) @exp(x)	返回x的自然对数值，其他底数用换底公式 返回e的x次方的值,因为e的数值没法敲入
其它	@abs(x) @sigh(x) @floor(x)	返回x的绝对值 返回x的符号值 返回x的整数部分,向靠近0的方向取整
比较大小	@smax(x1,x2,…,xn) @smin(x1,x2,…,xn)	返回其中的最大值 返回其中的最小值

例

y = @sin(3.14159) + @log(1024)/@log(2) + @abs(-10) + @exp(0);

集合操作函数

类别	函数名	作用
常用	@for(factory:a>0) @sum(factory:a)	循环 求和
有用	prod(factory:a) @max(factory:a) @min(factory:a)	求乘积 求最大值 求最小值
一般不用	@in(factory:a) @size(factory)	判断常数C是否在集合当中 返回工厂可生产矩阵的长度

例

model:
sets:
factory / 1..6 / : a;
endsets
data:a = 6,5,4,3,2,1;
enddata
prod = @prod(factory : a);
greater = @max(factory : a);
less = @min(factory : a);
in = @in(factory,5);
size = @size(factory);
end