二分图的最大匹配算法简析
资料来源: Snow_storm 学长。
有这么两个奇怪的工厂:工厂X只生产杯具,工厂Y只生产洗具 。最近,两个工厂决定将产品实行打包策略:即一个杯具搭配上一个洗具。但由于杯具和洗具的形状和功能各不相同,对于某个类别的杯具来说,只能搭配某些类型的洗具。现在,两个工厂的厂长大人想知道最多能成功的搭配多少对杯具与洗具。
类似于上面例子中提到的搭配问题,在图论中的有规范的名称:匹配。注意到,上面的例子中涉及到的物品只有两类(杯具与洗具),且问题只涉及杯具与洗具的匹配,我们把这种只涉及一种关系的匹配问题称为二分匹配问题。
现在,让我们理清一些概念。
二分图:若图G中的点可以分为X和Y两部分,且每部分内部无任何边相连,(可以想象一下,正常情况下是不会出现搞基的。)则称图G为二分图。
匹配:无公共点的边集合(可以想象一下结婚这个词汇)。
匹配数:边集中边的个数
最大匹配:匹配数最大的匹配。
如图1-1,展示的就是一个二分图:粗体线表示该二分图的一种匹配方式,不难发现,此时的匹配已经是最大匹配。

如何能得到一个二分图的最大匹配?运用简单的枚举:找出全部匹配,然后保留匹配数最多的。但是这个算法的时间复杂度为边数的指数级,时间上通常无法承受。因此,需要寻求一种更加高效的算法。由此便引出了匈牙利算法(hungary),这个算法的名字很有趣,它是由匈牙利数学家Edmonds于1965年提出的。
在正式的讲这个算法之前,不妨想一想,还有什么办法可以比较快速的计算出二分图的最大匹配?没错,网络的最大流算法可以搞定:我们需要增加额外的源汇点S,T,则对于图 1-1我们很容易得到如图1-2所示的网络模型,图中所有的边容量都为1,粗体箭头表示流从该边经过:

由此,问题得到了等价的转换:最大匹配数=最大流。若采用sap算法计算最大流,则时间复杂度为O(V2E),已经有了较高的效率。然则杀鸡焉用宰牛刀,实际上,我们没必要将问题复杂化,针对二分图的特殊性,我们可以采用效率更高,代码量更小的hungary算法解决。
由此,问题得到了等价的转换:最大匹配数=最大流。若采用sap算法计算最大流,则时间复杂度为O(V2E),已经有了较高的效率。然则杀鸡焉用宰牛刀,实际上,我们没必要将问题复杂化,针对二分图的特殊性,我们可以采用效率更高,代码量更小的hungary算法解决。
- 初始化匹配数cnt为1。
- 在图中寻找增广路,若无法找到任何增广路,则执行4,否则执行3。
- 将增广路的首尾两点设置为非未盖点,且将增广路上的边进行取反操作,cnt+1,执行2。
- 算法结束,当前的cnt即为最大匹配数。
对于上面提到的方法,用图 1-3的具体计算来展示其实现的过程:
(红色粗体边,表示匹配边;黑色细体边,表示未匹配边。天蓝色的点表示未盖点;靛蓝色的点表示非未盖点。且设节点编号≥0)
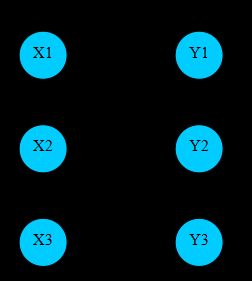
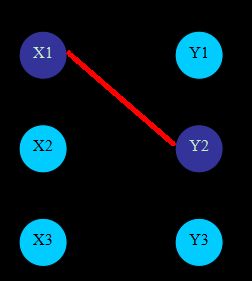
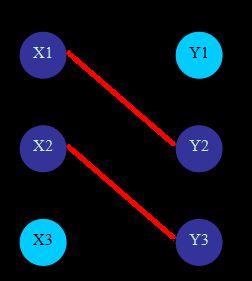
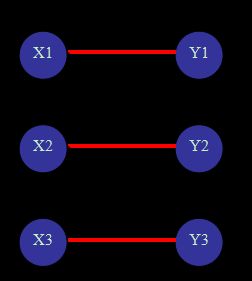
初始时,match[]都设为-1。因为可以从任意点开始匹配,则不妨按照点的编号顺序开始。对于X1,可以找到Y2与之匹配,且令match[Y2]=X1。同样的,对于X2,可以找到Y3与之匹配,且令match[Y3]=X2。当验证X3时,会发现唯一能够与其匹配的点Y3已经被匹配过了,则尝试修改之前的匹配方案:可以找到X2还可以与Y2匹配,但是同样的match[Y2]=X1≠-1,于是再去寻找X1是否能有新的匹配;可以发现X1还可以与Y1匹配,且match[Y1]=-1,则令match[Y1]=X1,match[Y2]=X2,match[Y3]=X3。得到了最终的最大匹配数=3。
上面这段话描述的是算法具体的操作步骤,现在不妨从增广路的角度来考虑:初始时,所有的点都是未盖点,匹配数cnt=0;我们很容易找到一条增广路X1-Y2,进行取反操作后,边(X1,Y2)由非匹配边变成了匹配边,cnt+1=1,且X1,Y2变成了非未盖点;继续寻找,我们也很容易的找到了增广路X2-Y2,进行取反操作后,边(X2,Y3)由非匹配边变成了匹配边,cnt+1=2,且X2,Y3变成了非未盖点。最后,可以找到增广路X3-Y3-X2-Y2-X1-Y1,同样进行取反操作,累加匹配数:cnt+1=3,同时X1,Y1也变成了非未盖点。注意到此时图中已经不存在任何增广路了,即该图的最大匹配数为3。
1 #define MAXN 500 //X部分的最大顶点数 2 #define MAXM 500 //Y部分的最大顶点数 3 #define _clr(x,y) memset(x,y,sizeof(x)) 4 5 int n,m; 6 7 int match[MAXM]; //标记数组 8 int g[MAXN][MAXM]; //邻接矩阵 9 10 bool used[MAXM]; //判重 11 12 bool find(int k) //dfs寻找增广路 13 { 14 for(int i=1;i<m;i++) 15 { 16 if(g[k][i] && !used[i]) 17 { 18 used[i]=true; 19 if(match[i]==-1 || find(match[i])) 20 { 21 match[i]=k; 22 return true; 23 } 24 } 25 } 26 return false; 27 } 28 29 int hungary() 30 { 31 int cnt=0; 32 _clr(match,-1); 33 for(int i=1;i<n;i++) 34 { 35 _clr(used,0); 36 if(find(i)) 37 { 38 cnt++; 39 } 40 } 41 return cnt; 42 }
以HDU2063为例: http://acm.hdu.edu.cn/showproblem.php?pid=2063

1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 #define N 505 5 int k, m, n; 6 int map[N][N], match[N]; 7 bool used[N]; 8 9 bool find (int x) 10 { 11 for (int i=1; i<=n; i++) 12 { 13 if (map[x][i] && !used[i]) 14 { 15 used[i] = true; 16 if (match[i]==-1 || find(match[i])) 17 { 18 match[i] = x; 19 return true; 20 } 21 } 22 } 23 return false; 24 } 25 26 void Hungary () 27 { 28 int cnt=0; 29 memset (match, -1, sizeof match); 30 for (int i=1; i<=m; i++) 31 { 32 memset (used, 0, sizeof used); 33 if (find(i)) cnt++; 34 } 35 printf ("%d\n",cnt); 36 } 37 int main() 38 { 39 int a, b; 40 while (~scanf ("%d",&k) && k) 41 { 42 memset (map, 0, sizeof map); 43 scanf ("%d%d",&m, &n); 44 while (k--) 45 { 46 scanf ("%d%d",&a, &b); 47 map[a][b] = 1; 48 } 49 Hungary(); 50 } 51 return 0; 52 }
资料来源:某位学长
