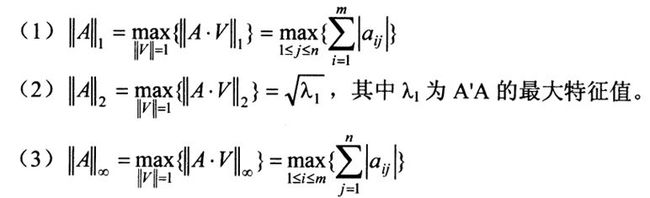MATLAB学习笔记（二）——主要是MATLAB的矩阵知识

PS：主要是讲解矩阵的相应的实现方法，其实MATLAB的很大一部分的优势，就是集成了矩阵级别的运算，并以此为特点，可以进行多维空间上的验证。

       让我们懂得了原来线性代数如此有用= - =。

（一）MATLAB矩阵

一、矩阵的建立

1、直接输入法创建：

       还可以有复数矩阵的建立，有两种方法：

    （1）直接按照直接输入法来建立矩阵，但是元素可以直接打成复数的形式（a+bj）

    （2）还有就是分别建立一个实部还有一个虚部的矩阵，然后通过（a+bj）就可以得到。

2、M文件建立矩阵

      就是把建立的矩阵存在一个文件里，下次直接调用就可以了。然后方法如下（下一篇日志会叙述）

3、利用冒号表达式建立一个向量

（1）e1:e2:e3

    其中e1为初始值，e2为步长，e3为终止值（只取到小于或者等于终止值就可以了），

    如果e2省略，那么默认步长为1；

（2）lidspace（a,b,n）

    a，b是生成向量的第一个和最后一个元素，n是元素总数。

4、建立大矩阵（由方括号中的小矩阵或者向量组合起来）

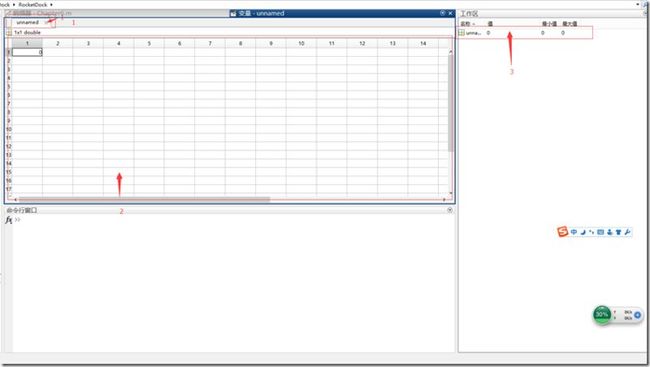
5、通过MATLAB集成的交互界面进行创建（最快）

（1）找到新建变量，并单击

（2）然后就可以进行新建变量了

        1处可以改变变量名字，2处可以进行矩阵的输入，3处可以查看矩阵在内存中是否保存，没有的话请按Ctrl+s。

二、矩阵的拆分

1、矩阵元素

（1）可以直接通过下标进行修改和访问，如果超过了原来矩阵的维度，会自动扩充，并且未填充的元素置为0。

（2）矩阵元素是按照列来存储，先第一列然后第二列。然后下标和序号可以一一对应，然后由对应的sub2ind和ind2sub求得

、

2、矩阵拆分

（1）用冒号表达式来获得子矩阵

a、a(  : ; j )表示取a矩阵的第j列的全部元素；同样的a（i;:）表示取a矩阵第i行的全部元素。也可以直接饮用对应下标取单独的元素。

b、里面可以嵌套冒号表达式，这样子就可以取出一个小的矩阵。例子如下

c、end表示最后一个数。

（2）利用空矩阵删除矩阵的元素

clear是把变量从空间中删除，而[]则是赋值成一个空的矩阵。

同样可以使用引用，进行数组的置空

三、特殊矩阵

1、通用的特殊矩阵：

zeros	产生0的矩阵
ones	产生1的矩阵
eye	产生对角矩阵
rand	产生0~1间均匀分布的随机矩阵
randn	产生矩阵为0，方差为1的标准正态分布随机矩阵

2、用于专门学科的特殊矩阵

（1）魔方矩阵（每行每列每对角线都相等）

           magic（n）: 生成n阶的魔方阵。

（2）范德蒙德矩阵

（3）希尔伯特矩阵

           hilb(n）                n阶希尔伯特矩阵

           invhilb（n）          n阶希尔伯特的逆矩阵

（4）托普利兹矩阵

           toeplitz(x,y）

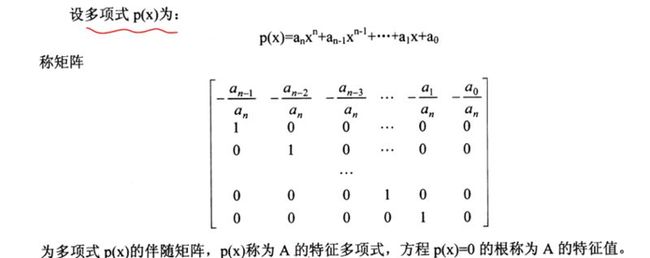
（5）伴随矩阵

 

 

（二）MATLAB运算

一、算术运算

1、基本算数运算

（1）加减

（2）乘法

（3）除法

（4）乘方

       这些运算主要都要服从矩阵的运算法则。维度不符合matlab会进行报错。

2、点运算

       格式是在正常的符号前面加上一个“.”就好了。

       运算的结果就是对矩阵中的每个元素相应的运算就好了，

二、关系运算

1、关系运算符：

<	小于
<=	小于等于
>	大于
>=	大于等于
==	等于
~=	不等于

2、运算法则：

（1）标量对标量：直接进行运算

（2）矩阵对矩阵：每个元素对应进行运算

（3）标量对矩阵：标量对每个元素进行运算

       最后是真的为“1”，假的为“0“。

PS：在这里记下一个求求余数的函数rem

三、逻辑运算

1、逻辑运算符。

2、运算法则同上。

PS：运算符的优先级排序：算术>关系>逻辑

3、其他相应的一些逻辑函数（通过名字来记住功能）

 

（三）矩阵分析

一、对角阵与三角阵

1、对角阵

（1）提取矩阵对角线上的元素:  diag(A), diag(A,k)

（2）构造对角阵:  diag(A)

       对每行每列进行相同乘数的运算，用对角阵相乘，左乘（对每行进行相乘），右乘（对每列进行相乘）

2、三角阵

（1）上三角阵

    triu(A)：将A变成一个上三角矩阵（下半边为0）

    triu(A,k)：将矩阵A的第k条对角线以上的元素

（2）下三角矩阵

    tril(A)

    tril(A,k)

二、矩阵的转置与旋转

1、矩阵的转置

（1）转置运算符是单撇号（’）

（2）作用就是求转置，但是请注意不是求逆矩阵。

2、矩阵的旋转

（1）运算符号：rot(A,k)

      就是将矩阵逆时针旋转k*90°的角度。如果单单旋转90°就可以直接省略k这个参数。

3、矩阵的左右翻转

（1）运算符号：fliplr(A)

4、矩阵的上下翻转

（1）运算符号：flipud(A)

三、矩阵的逆与伪逆

1、矩阵的逆

（1）定义：A·B=B·A=E，就称A和B互为逆矩阵。

（2）运算函数：inv(A)

（3）应用：可以用来求解线性方程组

2、矩阵的违逆

（1）定义：我们知道在矩阵不是满秩的时候是没有逆矩阵的。但是可以找到一个与A的转置矩阵A`同型的矩阵B，使得满足矩阵的逆的定义。此时称矩阵B为矩阵A的违逆。

（2）运算函数：pinv(A)

四、矩阵的行列式

  运算函数：det(A)

五、矩阵的秩与迹

1、矩阵的秩

（1）定义：就是一个矩阵的行数和列数线性无关的数目

（2）运算函数：rank(A)

2、矩阵的迹

（1）定义：就是矩阵对角阵上的元素之和。

（2）运算函数：trace(A)

六、向量和矩阵的范数

1、定义：用来度量矩阵或者向量在某种意义下的长度。

2、向量的3种常用范数以及计算函数

  

3、范数的三个性质：

（1）非负性

（2）齐次性

（3）满足施瓦茨不等式（a,b)<=(a,a)(b,b)

4、矩阵的范数及其计算函数

运算函数同向量的。

七、矩阵的条件数

（1）定义：在求解线性方程组时，如果系数的微小改变会导致最终结果的很大改变，称系数矩阵为病态矩阵，而不会导致最终结果的很大改变的话，则是良性矩阵，然后条件数便是来衡量这一情况的一个参数。

                条件数等于A的范数与A的逆矩阵的范数的乘积。这样的话，条件数总是大于1的，如果越接近于1的话，性能越好。

（2）函数为：

八、矩阵的特征值与特殊矩阵

 

（六）字符串

1、规则：

（1）用单引号括起来就是字符串。

（2）然后字符串可以写成一个矩阵，但是一个字母是一个元素，所以一定要保证矩阵的维数是正确的。

（3）如果字符串本身有单引号，就要加2个单引号。

（4）较长的字符串可以用字符串向量表示，及用[]括起来。

（八）稀疏矩阵

一、矩阵存储方式

1、完全储存方式：就是之前我们使用的方式

2、稀疏矩阵方式：

二、稀疏储存方式的产生：

1、将完全储存方式转化为稀疏矩阵的方式

（1）A=sparse(S)：将矩阵S转化为稀疏储存方式的矩阵A

（2）sparse的其他调用方式：

       sparse(m,n)：生成一个m*n的所有元素都是0的稀疏矩阵

       sparse(u,v,S)：u,v,S是3个等长的向量。S是要建立的稀疏矩阵的非零元素，u，v是行列下标，然后S是相应的元素值。

（3）其他操作的方式：

      [u,v,s]=find(A)：返回矩阵A中非零元素的下标和元素。

      full(A)：返回和稀疏储存矩阵A对应的完全储存方式矩阵。

2、产生稀疏储存矩阵