贪心算法--Dijkstra单源最短路径

今天兴致勃勃的开始做了贪心算法的第一道题目：Single-Source Shortest-Paths Problem

也就是所谓的单源最短路径，课件上有算法，但是代码实现起来还真是不容易（仅仅对于我这个菜鸟来说），下面是算法框架：

 设S为最短距离已确定的顶点集（看作红点集），V-S是最短距离尚未确定的顶点集（看作蓝点集）。
①初始化
   初始化时，只有源点s的最短距离是已知的(D(s)=0)，故红点集S{s} 。
②重复以下工作，按路径长度递增次序产生各顶点最短路径
    　在当前蓝点集中选择一个最短距离最小的蓝点来扩充红点集，以保证算法按路径长度递增的次序产生各顶点的最短路径。
    　当蓝点集中仅剩下最短距离为∞的蓝点，或者所有蓝点已扩充到红点集时，s到所有顶点的最短路径就求出来了。

---

 

 

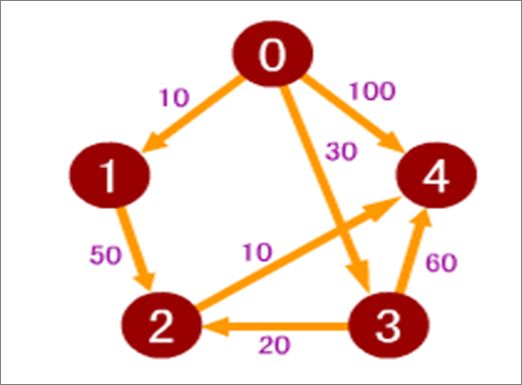
示例图形如下：

---

 

 

 

 

Q	u	S	临接点	d[1]	d[2]	d[3]	d[4]
{0，1，2，3，4}		Φ		∞	∞	∞	∞
{1，2，3，4}	0	{0}	1，4	10		30	100
{2，3，4}	1	{0,1}	2		60
{2，4}	3	{0,1,3}	4,2		50		90
{4}	2	{0,1,3,2}	4				60
Φ	4	{0，1，2，3，4}

 

 

有了这样思路下面就要来实现代码了：

下面是我自己写了三个小时的代码，可以输入0~4之间的任意数字，拿来给大家分享（高手别喷）:

 

#include <iostream>

#include <stdlib.h>

using namespace std;



#define MAX 1000000        //充当"无穷大"

#define LEN sizeof(struct V_sub_S)

#define N 5

#define NULL 0



int s;            //输入的源点

int D[N];        //记录最短路径

int S[N];        //最短距离已确定的顶点集

const int G[N][N] = {  {0, 10, MAX, 30, 100},

                                    {MAX, 0, 50, MAX, MAX},

                                    {MAX, MAX, 0, MAX, 10},

                                    {MAX, MAX, 20, 0, 60},

                                    {MAX, MAX, MAX, MAX, 0} };



typedef struct V_sub_S        //V-S链表

{

    int num;

    struct V_sub_S *next;

};



struct V_sub_S *create()

{

    struct V_sub_S *head, *p1, *p2;

    int n = 0;

    head = NULL;

    p1 = (V_sub_S *)malloc(LEN);

    p1->num = s;

    head = p1;

    for(int i = 0; i < N+1; i ++)

    {

        if(i != s)

        {

            ++ n;

            if(n == 1)

                head = p1;

            else

                p2->next = p1;

            p2 = p1;

            p1 = (V_sub_S *)malloc(LEN);

            p1->num = i;

            p1->next = NULL;

        }

    }

    free(p1);

    return head;

}



struct V_sub_S *DelMin(V_sub_S *head, int i) //删除链表中值为 i 的结点

{

    V_sub_S *p1, *p2;

    p1 = head;

    while(i != p1->num && p1->next !=NULL)

    {

        p2 = p1;

        p1 = p1->next;

    }

    p2->next = p1->next;

    return head;

}



void Dijkstra(V_sub_S *head, int s)

{

    struct V_sub_S *p;

    int min;

    S[0] = s;

    for(int i = 0; i < N; i ++)

    {

        D[i] = G[s][i];

    }

    for(int i = 1; i < N; i ++)

    {

        p = head->next;

        min = p->num;

        while(p->next != NULL)

        {

            if(D[p->num] > D[(p->next)->num])

                min = (p->next)->num;

            p = p->next;

        }

        S[i] = min;

        head = DelMin(head, min);

        p = head->next;

        while(p != NULL)

        {

            if(D[p->num] > D[min] + G[min][p->num])

            {

                D[p->num] = D[min] + G[min][p->num];

            }

            p = p->next;

        }

    }

}

void Print(struct V_sub_S *head)

{

    struct V_sub_S *p;

    p = head->next;

    while(p != NULL)

    {

        if(D[p->num] != MAX)

        {

            cout << "D[" << p->num << "]: " << D[p->num] << endl;

            p = p->next;

        }

        else

        {

            cout << "D[" << p->num << "]: " << "∞" << endl;

            p = p->next;

        }

    }

}



int main()

{

    struct V_sub_S *head;

    cout << "输入源点 s (0到4之间): ";

    cin >> s;

    head = create();

    Dijkstra(head, s);

    head = create();

    Print(head);

    system("pause");

    return 0;

}