bzoj（矩阵快速幂）

 

题意：定义Concatenate(1,N)=1234567……n。比如Concatenate(1,13)=12345678910111213。给定n和m，求Concatenate(1,n)%m。 （1=<n<=10^18,1<=m<=10^9）

思路：令f[n]表示Concatenate(1,n)。那么有：

f[i]=f[i-1]*10+(i-1)+1   1<=i<=9

f[i]=f[i-1]*100+(i-1)+1  10<=i<=99

……

因此可用矩阵加速：

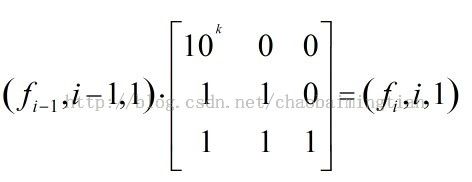
这样按位数分段来矩阵快速幂1~9，10~99，100~999......这里构造矩阵要注意细节；设上面两个矩阵分别为F,G;则要从F0开始；

这样刚好Fn=G^n*F0;如果是G^(n-1)*F1=Fn的话，在分段过程中会出错的（原因自己尽量想想）。

而F0={0,0,1},所以Fn=0*Gn.m[0][0]+0*Gn.m[0][1]+1*Gn.m[2][0]=Gn.m[2][0].

 

#include <cstdio>

#include <cstring>

#include <cmath>

#include <iostream>

#include <algorithm>

#include <queue>

#include <cstdlib>

#include <vector>

#include <set>

#include <map>

#define LL long long

#define inf 1<<30

#define N 100010

using namespace std;

struct matrix

{

    LL m[3][3];

}ans;

LL dig[20],n,mod;

matrix mult(matrix a,matrix b)

{

    matrix c;

    memset(c.m,0,sizeof(c.m));

    for(int i=0;i<3;i++)

    for(int k=0;k<3;k++)

    {

        if(a.m[i][k]==0)continue;

        for(int j=0;j<3;j++)

        {

            if(b.m[k][j]==0)continue;

            c.m[i][j]+=a.m[i][k]*b.m[k][j]%mod;

            c.m[i][j]%=mod;

        }

    }

    return c;

}

matrix quickmod(matrix a,LL n)

{

    matrix temp;

    memset(temp.m,0,sizeof(temp.m));

    for(int i=0;i<3;i++)temp.m[i][i]=1;

    while(n)

    {

        if(n&1)temp=mult(temp,a);

        a=mult(a,a);

        n>>=1;

    }

    return temp;

}

matrix solve(LL n,LL t)

{

    matrix x;

    x.m[0][0]=t%mod;x.m[0][1]=0;x.m[0][2]=0;

    x.m[1][0]=1;x.m[1][1]=1;x.m[1][2]=0;

    x.m[2][0]=1;x.m[2][1]=1;x.m[2][2]=1;

    return quickmod(x,n);

}



int main()

{

    dig[0]=1;

    for(int i=1;i<=18;i++)dig[i]=dig[i-1]*10;

    while(scanf("%lld%lld",&n,&mod)!=EOF)

    {

        memset(ans.m,0,sizeof(ans.m));

        for(int i=0;i<3;i++)

        ans.m[i][i]=1;

        for(int i=1;;i++)

        {

            LL left=dig[i-1];

            LL right=min(n,dig[i]-1);

            ans=mult(ans,solve(right-left+1,dig[i]));

            if(right==n)break;

        }

        printf("%lld\n",ans.m[2][0]);

    }

}

View Code