NOI2010 海拔（平面图最大流）

此题：

平面图最大流用的不是网络流算法，但是需要网络流的结论：最小割=最大流

【问题描述】 

YT 市是一个规划良好的城市，城市被东西向和南北向的主干道划分为 n×n 个区域。简

单起见，可以将 YT 市看作 一个正方形，每一个区域也可看作一个正方形。从而，YT 城市

中包括(n+1)×(n+1)个交叉路口和 2n×(n+1)条双向道路（简称道路），每条双向 道路连接主干

道上两个相邻的交叉路口。下图为一张 YT 市的地图(n = 2)，城市被划分为 2×2 个区域，包

括 3×3 个交叉路口和 12 条双向道路。

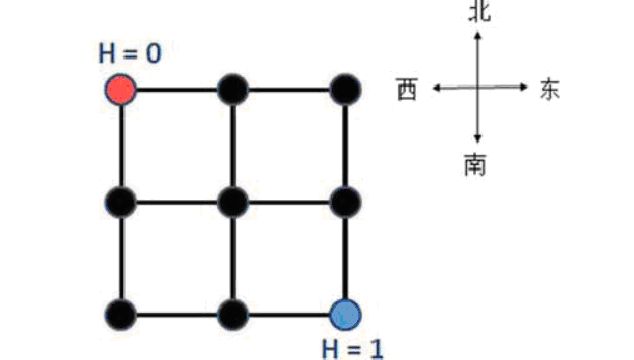
小 Z 作为该市的市长，他根据统计信息得到了每天上班高峰期间 YT 市每条道路两个方

向的人流量，即在高峰期间沿 着该方向通过这条道路的人数。每一个交叉路口都有不同的

海拔高度值，YT 市市民认为爬坡是一件非常累的事情，每向上爬 h 的高度，就需要消耗 h

的体力。如果 是下坡的话，则不需要耗费体力。因此如果一段道路的终点海拔减去起点海

拔的值为 h(注意 h 可能是负数)，那么一个人经过这段路所消耗的体力是 max{0, h}（这里

max{a, b}表示取 a, b 两个值中的较大值）。

小 Z 还测量得到这个城市西北角的交叉路口海拔为 0，东南角的交叉路口海拔为 1(如上

图所示)，但其它交叉路口的海拔高度都无法得知。小 Z 想知道在最理想的情况下（即你可

以任意假设其他路口的海拔高度），每天上班高峰期间所有人爬坡消耗的总体力和的最小值。

【输入格式】 

输入文件 altitude.in 第一行包含一个整数 n，含义如上文所示。

接下来 4n(n + 1)行，每行包含一个非负整数分别表示每一条道路每一个方向的人流量信

息。输入顺序：n(n + 1)个数表示所有从西到东方向的人流量，然后 n(n + 1)个数表示所有从

北到南方向的人流量，n(n + 1)个数表示所有从东到西方向的人流量，最后是 n(n + 1)个数表

示所有从南到北方向的人流量。对于每一个方向，输入顺序按照起点由北向南，若南北方向

相同时由西到东的顺序给出(参见样例输入)。

【输出格式】 

输出文件 altitude.out 仅包含一个数，表示在最理想情况下每天上班高峰期间所有人爬

坡所消耗的总体力和（即总体力和的最小值），结果四舍五入到整数。

全国青少年奥林匹克竞赛（NOI）2010 试题

Copyright © 2010 中国计算机学会, 版权所有.

【样例输入】 

1

1

2

3

4

5

6

7

8

【样例输出】 

3

【样例说明】 

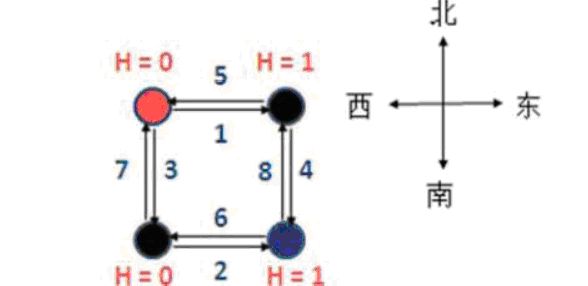
样例数据见下图。

 

 

最理想情况下所有点的海拔如上图所示。

【数据规模】 

对于 20%的数据：n ≤ 3；

对于 50%的数据：n ≤ 15；

对于 80%的数据：n ≤ 40；

对于 100%的数据：1 ≤ n ≤ 500，0 ≤ 流量 ≤ 1,000,000 且所有流量均为整数。

【提示】 

海拔高度不一定是整数。

【运行时限】 

2 秒。

【运行空限】 

512M。

 

第一眼看题目有木有很蛋疼。。海拔可以随便取，还不一定是整数。。。

但是想：找出图中海拔最高的点，如果它不是起止点，那么总是可以把它调小使得结果更优。那么最高点最后就必然为终点。同理可知最低点必然为起点。那么图中有没有可能存在小数使得结果更优呢？同样可以把小数向上或向下调整到1或0使得代价不增。

再有，所有海拔为0的点必然互相连通。为什么呢？显然，四面连接1的0如果使它取1必然使结果更优。同理可推海拔为1的点。

那么得到了大致的图后，很明显，就是一个最小割的问题了。

把每边消耗的体力设为这条边的流量，求出割，分成海拔分别为0和1的两块。

但是最后两点必超无疑。。。

有没有时效更高的做法呢？用最短路来求割。

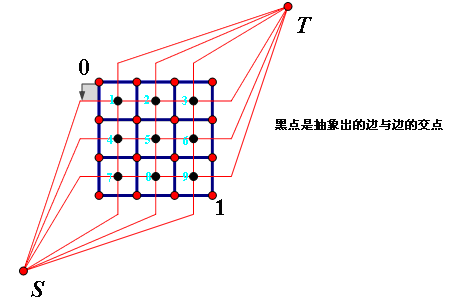
在题目所给图中的左下角和右上角加入源和汇，如下建立原图的对偶图（红色部分）：

 

摘自：http://blog.sina.com.cn/s/blog_86942b1401014ajk.html

可以看出，每一条最短路必然把地图“切成”两块，那么每条连接源和汇的路径就是一组合法的割了，求出最短路，就相当于求出最小割、

只要最短路，强烈建议编dij+heap，第一次想当然编了spfa倒二点4+s。。。不过敲了下dij+heap的模版还是很有感觉的。

最后的最后，不得不说下读入。。。什么南北东西的南方人表示理解不能。。。连个优先级都没搞清楚。结果建图的地方借用了上面blog中的做法。。。鸣谢、

对于每组n*(n+1)条边都是按照从左到右再从上到下给的。

搞定了读入，再建图就没有什么困难了。

 

 

代码：

View Code

 1 #include <cstdio>

 2 #include <cstdlib>

 3 #include <algorithm>

 4 #include <cstring>

 5 #define N 300000

 6 #define M 3000000

 7 using namespace std;

 8 int n,S,T,dis[N],head[N],next[M],to[M],len[M],cnt,size;

 9 struct HEAP

10 {

11     int x,d;

12 }heap[M];

13 inline void add(int u,int v,int w)

14 {

15     to[cnt]=v; len[cnt]=w; next[cnt]=head[u]; head[u]=cnt++;

16 }

17 int getnum(int x,int y)

18 {

19     return (x-1)*n+y;

20 }

21 inline bool cmp(const HEAP &a,const HEAP &b)

22 {

23     return a.d>b.d;

24 }

25 void read()

26 {

27     memset(head,-1,sizeof head);

28     cnt=0;

29     scanf("%d",&n);

30     S=0; T=n*n+1;

31     int a;

32     // 

33     for(int i=1;i<=n;i++) scanf("%d",&a),add(S,getnum(1,i),a);

34     for(int i=1;i<n;i++)

35         for(int j=1;j<=n;j++) 

36             scanf("%d",&a),add(getnum(i,j),getnum(i+1,j),a);

37     for(int i=1;i<=n;i++)

38         scanf("%d",&a),add(getnum(n,i),T,a);

39     // 

40     for(int i=1;i<=n;i++)

41     {

42         scanf("%d",&a),add(getnum(i,1),T,a);

43         for(int j=2;j<=n;j++) scanf("%d",&a),add(getnum(i,j),getnum(i,j-1),a);

44         scanf("%d",&a),add(S,getnum(i,n),a);

45     }

46     //

47     for(int i=1;i<=n;i++) scanf("%d",&a);

48     for(int i=1;i<n;i++)

49         for(int j=1;j<=n;j++) 

50             scanf("%d",&a),add(getnum(i+1,j),getnum(i,j),a);

51     for(int i=1;i<=n;i++) scanf("%d",&a);

52     //

53     for(int i=1;i<=n;i++)

54     {

55         scanf("%d",&a);

56         for(int j=2;j<=n;j++) scanf("%d",&a),add(getnum(i,j-1),getnum(i,j),a);

57         scanf("%d",&a);

58     }

59 }

60 void dijkstra()

61 {

62     memset(dis,0x3f,sizeof dis);

63     heap[1].x=S; heap[1].d=0; dis[S]=0; size=1;

64     int sta;

65     while(size)

66     {

67         sta=heap[1].x;

68         pop_heap(heap+1,heap+1+size,cmp);

69         size--;

70         for(int i=head[sta];~i;i=next[i])

71             if(dis[to[i]]>dis[sta]+len[i])

72             {

73                 dis[to[i]]=dis[sta]+len[i];

74                 size++;

75                 heap[size].x=to[i]; heap[size].d=dis[to[i]];

76                 push_heap(heap+1,heap+1+size,cmp);

77             }

78     }

79     

80     printf("%d\n",dis[T]);

81 }

82 int main()

83 {

84     read();

85     dijkstra();

86     system("pause");

87     return 0;

88 }