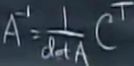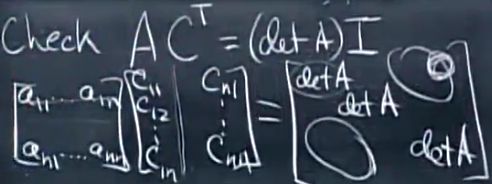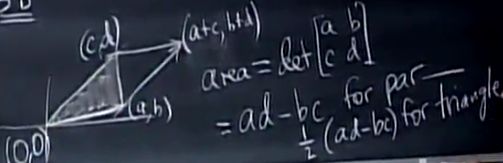线性代数导论20——克莱姆法则、逆矩阵、体积
本文是Gilbert Strang的线性代数导论课程笔记。课程地址: http://v.163.com/special/opencourse/daishu.html
第二十课时:克莱姆法则、逆矩阵、体积
本文
介绍行列式的应用,行列式用一个数值就包含所有信息。
先回顾上讲的内容:行列式的代数余子式表达式:
求逆矩阵公式
A的求逆矩阵公式:A-1=(1/detA)*CT 。(C是由代数余子式组成的矩阵)
CT是原矩阵A的伴随矩阵,伴随矩阵11元素就是原矩阵11元素的代数余子式,由于转置的缘故,伴随矩阵12的元素是原矩阵21元素的代数余子式。
公式的证明:
只需检验A乘以它的上述公式的逆是否等于单位阵,即:AC
T=(detA)I, AC
T的计算结果是,主对角线上的元素均为detA(因为元素和代数余子式都来自同一行,根据行列式的代数余子式公式可得),非对角线上的元素均为0(矩阵某行乘以另一行的代数余子式结果为0,比如A的第一行乘以最后一行的代数余子式,这相当于(比方)求一个特殊矩阵的行列式,特殊矩阵的第一行和最后一行相等(某两行相等的特殊矩阵的行列式必为0)。)。
(我们记得以前矩阵的逆是如何求的,通常把矩阵变为增广矩阵,然后将左边变为单位矩阵,右边就变为了逆矩阵)
克莱姆法则Cramer RULE
观察C
Tb,C
T中每行代数余子式乘以向量b中的数字,让人联想这是在求某个矩阵B的行列式,如下:
B1矩阵是一个:用向量b替换矩阵A的第一列得到的矩阵,因为这样的矩阵求行列式将得到CTb第一行乘以b的值(CTb的第一行是A矩阵的第一列的代数余子式,这个值正是detB1)。Bj是一个用向量b替换矩阵A的第j列得到的矩阵。
克莱姆法则的作用主要是提供一种代数表达式,而不是一种算法,不建议使用它来计算。
通过行列式求体积
行列式的值等于某几何体的体积
待证明命题:
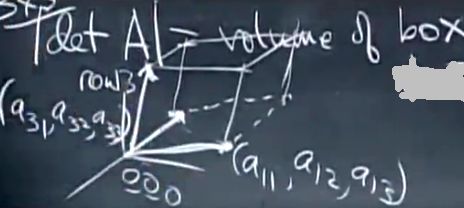
行列式的绝对值等于一个箱子(平行N面体)的体积。3×3的行列式是三维空间箱子(平行6面体,由三条边觉得箱子的样子、体积)的体积。
当A=I时,命题明显成立,箱子是单位立方体。
当A=Q为正交矩阵(非I时)时,三个列向量是标准正交基。箱子通过行向量还是列向量定义都无所谓,因为转置的行列式不变,正交矩阵对于的箱子是什么形状?箱子还是单位立方体,它和单位矩阵的立方体的区别是它被旋转了(立方体的形状大小不变,只是位置随着标准正交基的位置旋转了)。
Q
T
Q=I,det
Q
T
Q=detI=det
Q
T
* det
Q =
(detQ)
2 = 1,因此detQ=1或-1。
当箱子为长方体时,假设是由两个单位立方体组成的,此时体积是原来的2倍,对于矩阵A的第一行是原来的两倍,根据行列式性质3(1),那么行列式也是原来的2被。
性质3(2)告诉我们,这个性质是推出普通的箱子的体积也是行列式的绝对值的线索,有待证明。
对于2维平面,平行四边形的面积为行列式。三角形的面积就为它的一半。
假设三角形的顶点并不在原点上,它的面积如下,求如下矩阵的行列式时,可以先对它进行消元将前两行变成:
(x2-x1,y2-y1,0),(x3-x2,y3-y2,0),那么这个行列式就是求第三列的代数余子式,实际上就是求矩阵(x2-x1,y2-y1 ),(x3-x2,y3-y2)的行列式。这两个向量表示这两条边。