Codeforces Round #217前三题

Little Petya is learning to play chess. He has already learned how to move a king, a rook and a bishop. Let us remind you the rules of moving chess pieces. A chessboard is 64 square fields organized into an 8 × 8 table. A field is represented by a pair of integers (r, c)— the number of the row and the number of the column (in a classical game the columns are traditionally indexed by letters). Each chess piece takes up exactly one field. To make a move is to move a chess piece, the pieces move by the following rules:

A rook moves any number of fields horizontally or vertically.
A bishop moves any number of fields diagonally.
A king moves one field in any direction — horizontally, vertically or diagonally.

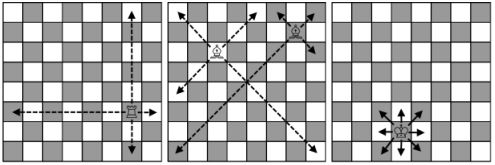$Codeforces Round #217前三题_第1张图片$ The pieces move like that

Petya is thinking about the following problem: what minimum number of moves is needed for each of these pieces to move from field(r₁, c₁) to field (r₂, c₂)? At that, we assume that there are no more pieces besides this one on the board. Help him solve this problem.

Input

The input contains four integers r₁, c₁, r₂, c₂ (1 ≤ r₁, c₁, r₂, c₂ ≤ 8) — the coordinates of the starting and the final field. The starting field doesn't coincide with the final one.

You can assume that the chessboard rows are numbered from top to bottom 1 through 8, and the columns are numbered from left to right 1 through 8.

Output

Print three space-separated integers: the minimum number of moves the rook, the bishop and the king (in this order) is needed to move from field (r₁, c₁) to field (r₂, c₂). If a piece cannot make such a move, print a 0 instead of the corresponding number.

Sample test(s)

input
4 3 1 6

output
2 1 3

input
5 5 5 6

output
1 0 1

题目大意：从一个点到另一个点，经过三种变换，问分别用每种变换可以到的最小步数。第一种是横着竖着走，答案直接分为1，2即可。第二种斜着走，答案分为1 2 0三种，0表示到达不了，画一个方格走一下就懂了。坑在了第三种前面两种每次走的路程任意，而第三种每次只能走一步，可以斜着横着竖着走。竟然没心没肺的写了个bfs......直接比较横纵坐标差值，谁大就可以了。。这个题目和昨天晚上打的cf题目很相似，不过昨天晚上那个需要判断越界。

题目地址：A. Rook, Bishop and King

AC代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int a,b,c,d;
int visi[10][10];
int res[10][10];
int dir[8][2]={{-1,0},{1,0},{0,1},{0,-1},{-1,1},{-1,-1},{1,1},{1,-1}};

void bfs()
{
    queue<int> mq;
    mq.push(a*10+b);
    //cout<<a<<" "<<b<<"dsd"<<endl;
    memset(visi,0,sizeof(visi));
    visi[a][b]=1;
    memset(res,0,sizeof(res));

    while(!mq.empty())
    {
        int cur=mq.front();
        mq.pop();
        int tx,ty;
        tx=cur/10,ty=cur%10;
        //cout<<tx<<" "<<ty<<endl;

        if(tx==c&&ty==d)
        {
            //cout<<"dsa"<<endl;
            return;
        }
        int cx,cy;
        for(int i=0;i<8;i++)
        {
            cx=tx+dir[i][0],cy=ty+dir[i][1];
            if(cx>=1&&cx<=8&&cy>=1&&cy<=8&&!visi[cx][cy])
            {
                res[cx][cy]=res[tx][ty]+1;
                visi[cx][cy]=1;
                mq.push(cx*10+cy);
            }
        }
   }
}

int main()
{
    int s1,s2;
    while(cin>>a>>b>>c>>d)
    {
        if(a==c||b==d)
            s1=1;
        else
            s1=2;

        if(a+b==c+d||a+d==b+c)
            s2=1;
        else if(abs(a+b-c-d)%2==0)
            s2=2;
        else
            s2=0;
        bfs();
        printf("%d %d %d\n",s1,s2,res[c][d]);
    }
    return 0;
}

Lately, a national version of a bingo game has become very popular in Berland. There are n players playing the game, each player has a card with numbers. The numbers on each card are distinct, but distinct cards can have equal numbers. The card of the i-th player contains m_i numbers.

During the game the host takes numbered balls one by one from a bag. He reads the number aloud in a high and clear voice and then puts the ball away. All participants cross out the number if it occurs on their cards. The person who crosses out all numbers from his card first, wins. If multiple people cross out all numbers from their cards at the same time, there are no winners in the game. At the beginning of the game the bag contains 100 balls numbered 1 through 100, the numbers of all balls are distinct.

You are given the cards for each player. Write a program that determines whether a player can win the game at the most favorable for him scenario or not.

Input

The first line of the input contains integer n (1 ≤ n ≤ 100) — the number of the players. Then follow n lines, each line describes a player's card. The line that describes a card starts from integer m_i (1 ≤ m_i ≤ 100) that shows how many numbers the i-th player's card has. Then follows a sequence of integers a_i, 1, a_i, 2, ..., a_{i, m_i} (1 ≤ a_i, k ≤ 100) — the numbers on the i-th player's card. The numbers in the lines are separated by single spaces.

It is guaranteed that all the numbers on each card are distinct.

Output

Print n lines, the i-th line must contain word "YES" (without the quotes), if the i-th player can win, and "NO" (without the quotes) otherwise.

Sample test(s)

input
3
1 1
3 2 4 1
2 10 11

output
YES
NO
YES

input
2
1 1
1 1

output
NO
NO

题目大意：每次有n个人，每个人手上拿了若干卡片，每个卡片编号不一样，当然同一个人手里的编号不会重复。然后一个人在点号，他报到哪一个号，持有相应卡片的人就把那张卡片划掉，最先被划掉所有卡片的人会得到奖励，问谁有可能获得奖励，如果可能输出yes，否则输出no。

解题思路：可以直接判断集合包含子集的问题，每个人是一个集合，集合里的元素就是自己的卡片，可以包含别人的集合，那么你就是no。

题目地址：A. Rook, Bishop and King

AC代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;

int a[102];
int visi[102][102];
int t[102];
int n;

int cal(int a,int b)
{
    int i;
    for(i=1;i<=100;i++)
    {
        if(!visi[a][i]&&visi[b][i]) return 0;
    }
    return 1;
}

void solve()
{
    int i,j;
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=n;j++)
        {
            if(i==j) continue;
            if(cal(i,j))
                t[i]=0;
        }
    }
}

int main()
{
    int d,i,x,j;
    while(cin>>n)
    {
        memset(visi,0,sizeof(visi));
        for(i=1;i<=n;i++)
        {
            scanf("%d",&d);
            for(j=1;j<=d;j++)
            {
                scanf("%d",&x);
                visi[i][x]=1;
            }
        }

        for(i=1;i<=n;i++)
            t[i]=1;
        solve();

        for(i=1;i<=n;i++)
        {
            if(t[i]==1)
                puts("YES");
            else
                puts("NO");
        }
    }
    return 0;
}

A Christmas party in city S. had n children. All children came in mittens. The mittens can be of different colors, but each child had the left and the right mitten of the same color. Let's say that the colors of the mittens are numbered with integers from 1 to m, and the children are numbered from 1 to n. Then the i-th child has both mittens of color c_i.

The Party had Santa Claus ('Father Frost' in Russian), his granddaughter Snow Girl, the children danced around the richly decorated Christmas tree. In fact, everything was so bright and diverse that the children wanted to wear mittens of distinct colors. The children decided to swap the mittens so that each of them got one left and one right mitten in the end, and these two mittens were of distinct colors. All mittens are of the same size and fit all the children.

The children started exchanging the mittens haphazardly, but they couldn't reach the situation when each child has a pair of mittens of distinct colors. Vasily Petrov, the dad of one of the children, noted that in the general case the children's idea may turn out impossible. Besides, he is a mathematician and he came up with such scheme of distributing mittens that the number of children that have distinct-colored mittens was maximum. You task is to repeat his discovery. Note that the left and right mittens are different: each child must end up with one left and one right mitten.

Input

The first line contains two integers n and m — the number of the children and the number of possible mitten colors (1 ≤ n ≤ 5000, 1 ≤ m ≤ 100). The second line contains n integers c₁, c₂, ... c_n, where c_i is the color of the mittens of the i-th child (1 ≤ c_i ≤ m).

Output

In the first line, print the maximum number of children who can end up with a distinct-colored pair of mittens. In the next n lines print the way the mittens can be distributed in this case. On the i-th of these lines print two space-separated integers: the color of the left and the color of the right mitten the i-th child will get. If there are multiple solutions, you can print any of them.

Sample test(s)

input
6 3
1 3 2 2 1 1

output
6
2 1
1 2
2 1
1 3
1 2
3 1

input
4 2
1 2 1 1

output
2
1 2
1 1
2 1
1 1

题目大意：袜子配套，要求尽量多的袜子配对了以后品种不一样。

解题思路：自己思路是正确的，开始还以为自己哪里想错了呢，我觉得就是贪心的思想，先排个序，把小号先放一下，不过左右支要标号，然后再放大号的，详解见代码。

题目地址：C. Mittens

AC代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;

int a[105];
int p[5002][2];

int main()
{
    int n,m,i,d;
    while(cin>>n>>m)
    {
        memset(a,0,sizeof(a));
        memset(p,0,sizeof(p));
        for(i=1;i<=n;i++)
        {
            scanf("%d",&d);
            a[d]+=2;      //先把各种类的统计出来
        }

        int t=1;
        int x=0;
        while(1)      //先放小号的
        {
            if(t==n+1) break;
            for(i=1;i<=m;i++)
            {
                if(a[i]>0)
                {
                    a[i]--;
                    p[t++][x]=i;
                    if(x==0) x=1;
                    else x=0;
                    break;
                }
            }
        }

        x=1;
        int flag=0;
        t=1;
        while(1)     //再放大号的
        {
            if(t==n+1) break;
            for(i=1;i<=n;i++)
            {
                if(a[i]>0)
                {
                    a[i]--;
                    p[t++][x]=i;
                    if(x==0) x=1;
                    else x=0;
                    break;
                }
            }
        }

        int ans=0;
        for(i=1;i<=n;i++)
        {
            if(p[i][0]!=p[i][1])
                ans++;
        }

        cout<<ans<<endl;
        for(i=1;i<=n;i++)
        {
            printf("%d %d\n",p[i][0],p[i][1]);
        }
    }
    return 0;
}

/*
5 3
1 1 2 2 3
10 3
1 1 1 2 2 2 2 2 2 3
*/

Codeforces Round #217前三题

你可能感兴趣的:(codeforces)