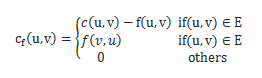算法系列笔记10(有关图的算法三—最大流与二分图)

本次主要记录流网络以及最大流的简单概念(以后可能会将最大流的实现算法补充)，重点讲解用匈牙利算法来求二分图的最大匹配。

1：流网络

流网络是G(V, E)是一个有限的有向图，它的每条边(u, v)∈E都有一个非负值实数的容量c(u, v)≥0。如果(u, v)不属于E，我们假设c(u, v) = 0。我们区别两个顶点：

一个源点s和一个汇点t.。并假定每个顶点均处于从源点到汇点的某条路径上。

形式化的定义：一道网络流是一个对于所有结点u和v都有以下特性的实数函数:：满足下面两条性质：

容量限制：0≤f(u,v)≤c(u,v)。

流量守恒：对于所有节点除了源点s和汇点t，净流量都等于0，即进入该结点的流和出该结点的流量相等。

这个网络的流量就是：

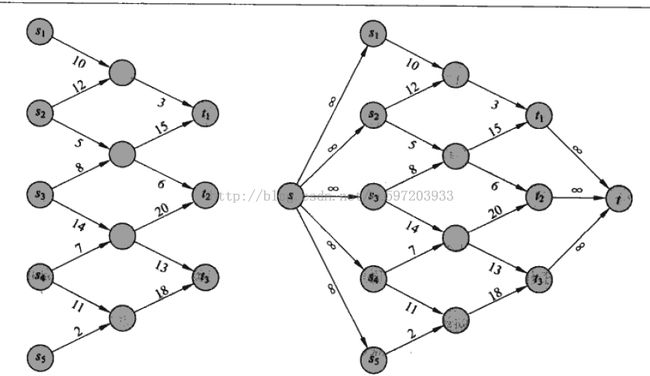
此外当然多源点和多汇点的流网络可以转换为只有一个源点和汇点的普通网络。

如图：

2：最大流——Ford-Fulkerson方法

最大流就是寻找一个流使得上式(1)达到最大。Ford-Fulkerson是方法而不是算法，因为它包含了几种运行时间不相同的实现。

概念:

(1)残存网络

残存网络G_f是由那些仍有空间对流量进行调整的边构成。计算公式如下：

注意:通常当c_f(u,v) = 0，我们不把它加入到残存网络中。

(2)增广路径

增广路径p是残存网络G_f中一条从源点s到汇点的简单路径。一条增广路径p上能够为每条边增加流量的最大值为路径p的残存容量。

如下图b)中的残存网络的s->v2->v3->t的残存容量就是4。一个流为最大流当且仅当其残存网络中不包含任何增广路径了。

例子：

(3)切割

任何切割的净流量的值都是等于|f|的值，不会超过G的任意切割的容量。一个网络的最小切割就是整个网络中容量最小的切割。

(4)最大流最小切割定理

基本的Ford-Fulkerson方法的伪代码：

现在的关键就是如何寻找残存网络中的增广路径。其中包括很多算法。比如：Emonds-Karp算法就是在残存网络中选择的增广路径是一条从源点s到汇点t的最短路径。

这里假设每条边的权重都为1.其时间复杂度为O(VE^2).此外，推送-重贴标签算法的时间复杂度为O(V^2E).而前置重贴标签算法的时间复杂度为O(V^3).

3:二分图

二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集L  和  R ，使得每一条边都分别连接 L 、R  中的顶点。如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。

图1 是一个二分图。 为了清晰，我们以后都把它画成图2 的形式.

匹配：在图论中，一个「匹配」（matching）M是一个边的集合，其中任意两条边都没有公共顶点。

例如，图3、图 4 中红色的边就是图 2的匹配。M中最多有一条边与v相连。

        

饱和与非饱和：  
        若匹配M的某条边与顶点v关联，则称M饱和顶点v，并且称v是M-饱和的，否则称v是M-不饱和的。  

或者称v是M匹配的。

我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。

例如图3中 1、4、5、7为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。

图 4是一个最大匹配，它包含 4条匹配边。

完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。

图4是一个完美匹配。显然，

完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，

添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。

是否可能让所有男孩和女孩两两配对，

使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。如果换一个说法：

最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。

基本概念讲完了。求解最大匹配问题的一个算法是匈牙利算法，下面讲的概念都为这个算法服务。

交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。

增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），

则这条交替路称为增广路（agumentingpath）。

例如，图5中的一条增广路如图6所示（图中的匹配点均用红色标出）：增广路有一个重要特点：非匹配边比匹配边多一条。

因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。

由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。

交换后，图中的匹配边数目比原来多了1条。我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。

找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。

匈牙利算法伪代码：

bool 寻找从k出发的对应项出的可增广路
{
	while (从邻接表中列举k能关联到顶点j)
	{
		if (j不在增广路上)
		{
			把j加入增广路;
			if (j是未盖点 或者 从j的对应项出发有可增广路)
			{
				修改j的对应项为k;
				则从k的对应项出有可增广路,返回true;
			}
		}
	}
	则从k的对应项出没有可增广路,返回false;
}
 
void 匈牙利hungary()
{
	for i->1 to n
	{
		if (则从i的对应项出有可增广路)
			匹配数++;
	}
	输出 匹配数;
}

以下是用分别以关联矩阵和邻接表存储的匈牙利算法的实现。时间复杂度为O(VE)。

邻接表：

/*这里只针对有向图，且已经二分好了*/

#include<iostream>
#include<cstring>
using namespace std;
//定义链表
struct link{
	int data;//存放数据
	link* next;//指向下一个节点
	link(int n);
};
link::link(int n){
	data = n;
	next = NULL;
}
int n1, n2, m, ans=0;
int result[101];             //记录n1中的点匹配的点的编号
bool state[101];              //记录n1中的每个点是否被搜索过
link *head[101];         //记录n2中的点的邻接节点
link* last[101];             //邻接表的终止位置记录
//判断能否找到从节点n开始的增广路
bool find(const int n){
	link *t = head[n];
	while(t != NULL){       //n仍有未查找的邻接节点时
		if(!(state[t->data])){     //如果邻接点t->data未被查找过
			state[t->data]=true;      //标记t->data为已经被找过
			if((result[t->data]==0)|| (find(result[t->data]))){         
			    //如果t->data不属于前一个匹配M 	//如果t->data匹配到的节点可以寻找到增广路
				result[t->data]=n;//那么可以更新匹配M'，其中n1中的点t->data匹配
				return true;//返回匹配成功的标志
			}
		}
		t=t->next;//继续查找下一个n的邻接节点
	}
	return false;
}
int main(){
	int t1 = 0, t2 = 0;
	cin >> n1 >> n2 >> m;
	for(int i=0; i<m; i++){
		cin>>t1>>t2;
		// last和head都是全局变量 内容都初始化为NULL了，
		//如果为局部变量，比较前必须要初始化为NULL
		if(last[t1]==NULL)  
			last[t1]=head[t1]=new link(t2);     
		else
			last[t1]=last[t1]->next=new link(t2);
	}
	for(int i=1; i<=n1; i++){
		memset(state,0,sizeof(state));
		if(find(i))ans++;
	}
	cout<<ans<<endl;
	return 0;
}

关联矩阵：

#include<iostream>
#include<cstring>
using namespace std;
int map[105][105]; // 关联矩阵
int visit[105], flag[105];   // 相当于邻接表中state和result
int n,m;
bool dfs(int a){
	for(int i=1; i <= n; i++){
		if(map[a][i] && !visit[i]){
			visit[i]=1;
			if(flag[i] == 0||dfs(flag[i])){
				flag[i] = a;
				return true;
			}
		}
	}
	return	false;
}
int	main(){
	while(cin >> n >> m){
	memset(map, 0, sizeof(map));
	for(int i=1; i<=m; i++){
		int x,y;
		cin >> x >> y;
		map[x][y]=1;
	}
	memset(flag, 0, sizeof(flag));
	int result=0;
	for(int i=1; i <= n;i++){
		memset(visit, 0, sizeof(visit));
		if(dfs(i)) result++;
	}
	cout << result <<endl;
	}
	return 0;
}

注意：寻找二分图的最大匹配算法-匈牙利算法，说白了就是最大流算法，但是它根据二分图的这个问题的特点，把最大流算法做了简化，

提高了效率。当然我们仍然可以使用传统的最大流算法。此时需要加一个源点s和汇点t，容量均设为1。

边为s到左边L集合顶点的边和R集合到t顶点的边得到一个网络流G1，M是图G的一个匹配当且仅当f是G1的一个整数值的流，并且M=|f|。

参考文献：

1：http://blog.csdn.net/pi9nc/article/details/11848327二分图的最大匹配、完美匹配和匈牙利算法

2：http://blog.csdn.net/akof1314/article/details/4421262匈牙利算法

3：http://baike.baidu.com/link?url=wLE9pjsJ8qpft_JwAKrQaV-eeD9p1ZsivZYReGaVoQxhsTI6cTDZMvALGKmFsGCLwdRI05VEuIkgxsZsai0taa百度百科

4：http://blog.csdn.net/china8848/article/details/2287769