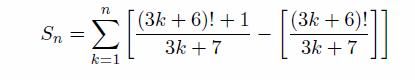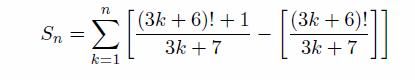- Codeforces Round 969 (Div. 2) C. Dora and C++ (裴蜀定理)
致碑前繁花
刷题记录c语言c++开发语言
什么?竟然是裴蜀定理。。。由于这里给出了a和b两个数,我们或许可以想到使用同样是需要给出两个定值的裴蜀定理,即:如果给定xxx和yyy,那么一定有ax+by=gcd(x,y)ax+by=gcd(x,y)ax+by=gcd(x,y)。所以在这时候我们就可以让输入的所有数都去对gcd(a,b)gcd(a,b)gcd(a,b)取模,这样就能够得到所有数的最简形式(可以当成是让所有数尽可能消去aaa和bb
- 偏偏是个煽情雨季
TX故事
从小到大,没经历过什么大起大落,一切都被安排得妥当。遇见深邃的人,继而平平淡淡,幼稚地为了和某人一样,近了视,继而迷迷糊糊。今天人手一部手机,就算戴好眼镜瞪大眼睛,各种原则定理还是听不下去,究竟美好的东西会不会反噬我?想写写文看看字,画好蓝图,离开条条框框,摆脱“不值得定律”里的一人一物,可责任心也得保留住。这一秒钟,注定只能放空,下雨天,操的心总是重一点,窗外雾气重,路面滑,各个人健康与安全都重
- (凸集)表示定理
流星落黑光
表示定理设为非空多面集,则有:(1)极点集非空,且存在有限个极点(2)极方向集合为空集的充要条件是S有界,若S无界,则存在有限个极方向(3)的充要条件是:证明略。解释:*1:对一个有限多面体的表面,并不需要极方向(极方向只存在与无限情况!),显然任意一个表面上的点都在某个平面上,可由这个平面的端点(即有限个极点)表示。对一个无限多面体表面,若一个点在一个无限大的面上,这个无限大的面也可由有限条线段
- 【机器学习】朴素贝叶斯
可口的冰可乐
机器学习机器学习概率论
3.朴素贝叶斯素贝叶斯算法(NaiveBayes)是一种基于贝叶斯定理的简单而有效的分类算法。其“朴素”之处在于假设各特征之间相互独立,即在给定类别的条件下,各个特征是独立的。尽管这一假设在实际中不一定成立,合理的平滑技术和数据预处理仍能使其在许多任务中表现良好。优点:速度快:由于朴素贝叶斯仅需计算简单的概率,训练和预测的速度非常快。适用于高维数据:即使在特征数量多的情况下,朴素贝叶斯仍然表现良好
- 学习二十大报告精神,做新时代青年。
梁亮亮
党的二十大是在全党全国各族人民全面建成社会主义现代化国家新征程、进入第二个百年奋斗目标的关键时刻召开的一次重要会议,对于党和国家发展史来说具有重要里程碑意义。青年强则国家强,作为新时代的青年,我们要坚定不移听党话跟党走,立志做有理想、敢担当、能吃苦、能奋斗的新时代好青年,就是要牢记“四个意识”、坚定理想信念。“总开关”上不怕下尖子,“总闸门”上不留空间;一个人能成长为一名合格建设者,其实就是站在共
- 【C语言】素数的判断方法----多方法详细分析
gugugu.
C/C++开发语言c语言开发语言
前言素数的判断方法是我们在写程序的过程中经常碰到的问题,今天给大家带来素数的一些判断方法。一、什么是素数?质数(primenumber)又称素数,有无限个。一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,换句话说就是该数除了1和它本身以外不再有其他的因数;否则称为合数。根据算术基本定理,每一个比1大的整数,要么本身是一个质数,要么可以写成一系列质数的乘积;而且如果不考虑这些质数在乘积中
- 【04】深度学习——训练的常见问题 | 过拟合欠拟合应对策略 | 过拟合欠拟合示例 | 正则化 | Dropout方法 | Dropout的代码实现 | 梯度消失和爆炸 | 模型文件的读写
花落指尖❀
#深度学习深度学习人工智能目标检测神经网络cnn
深度学习1.常见的分类问题1.1模型架构设计1.2万能近似定理1.3宽度or深度1.4过拟合问题1.5欠拟合问题1.6相互关系2.过拟合欠拟合应对策略2.1问题的本源2.2数据集大小的选择2.3数据增广2.4使用验证集2.5模型选择2.6K折交叉验证2.7提前终止3.过拟合欠拟合示例3.1导入库3.2数据生成3.3数据划分3.4模型定义3.5辅助函数3.6可视化4.正则化4.1深度学习中的正则化4
- 金融三定理
学生行之
Timevalueofmoney资金的聚集风险——保险:让社会分担分散个体的风险风险——股票:让更多人“利益共享,风险共担”风险——风投、创投:让社会分担创业创新风险明白:a时间的价值是切切实实可以看的到!b银行低利率吸收存款,国家发行债券,做基础建设c个人幼年,青年,壮年,老年如何配置资产抵御不同时期的风险!
- 赏析微课堂之达达主义(一)
鼎典美育卷卷老师
鼎典理念:让孩子拥有发现美和独立思考的品质。图片发自App2018.12.25今日赏析微课堂分享~达达艺术1916~1924年在欧美许多城市兴起的一种虚无主义艺术运动。是战后欧洲一些年轻的艺术家厌倦战争、彷徨、失望以及在艺术上否定理性和传统文化、崇拜虚无主义的精神产物。其创作方法主要通过照片剪接或与纸片、抹布拼贴,去追求艺术表现的偶然性。作品怪诞奇特,令人惊惑不解。法国画家马塞尔·杜尚是达达主义的
- 2021-10-03
心心向善
南无羌佛《世法哲言》浅释(二十四)慧海之库与物质之仓是为反量也,慧库无为转无量,多用之反增之。物仓储存乃无常,施之减之,故无为乃大,大在无量,无常乃微,微在消然。如果把人的智慧聪明的储藏境比做一个仓库的话,那么它与储存物质的仓库恰是相对的反量。智慧聪明的仓库属於无为转无量,即以无为的定理转无量的境界,所起的作用的是越用就越多,也就是说,一个人的才智聪明,是越用越聪明,越锻炼反应力就越快,越进步、聪
- 4.3万字详解PHP+RabbitMQ(AMQP协议、通讯架构、6大模式、交换机队列消息持久化、死信队列、延时队列、消息丢失、重复消费、消息应答、消息应答、发布确认、故障转移、不公平分发、优先级、等)
小松聊PHP进阶
laravelPHPphp架构服务器中间件后端laravelrabbitmq
理论(后半部分有实操详解)哲学思考易经思维:向各国人讲述一种动物叫乌龟,要学很久的各国语言,但是随手画一个乌龟,全世界的人都能看得懂。道家思维:努力没有用(指劳神费心的机械性重复、肢体受累、刻意行为),要用心(深度思考、去感悟、透过现象看本质)才有用。举例:类似中学做不出来的几何题的底层原理:不是不知道xx定理或公式(招式),而是不知道画辅助线的思路(内功)。总结:万事万物、用道家思维思考本质与规
- 着力建设一支德才兼备的高质量干部队伍
dc7bce189fd7
党章对加强党的执政能力建设提出了明确要求,党的执政能力的提高,党的建设的加强,关键在党的干部素质的提高上,也就是要有一支善于治国理政的高素质干部队伍。干部队伍的素质如何,对于保持党的先进性,提高党的执政能力,做好各项工作,具有决定性的意义。坚定理想信念,是好干部第一位的标准,以习近平新时代中国特色社会主义思想为指引,在思想认识上毫不动摇坚定道路、理论、制度、文化自信,在政治实践中一以贯之拥护党的领
- 践行青春誓言 建功立业新时代
玉面狐狸在偷塔
入职半月以来,逐渐适应了乡镇基层的工作调性,结合专业所学谈谈我对选调生身份的几点体会。一是,“选”之于党,选调生意味着要信念坚定,对党忠诚。作为从万千考生中选拔出的年轻力量,选调生不能辜负党和人民的期望,要信念坚定、对党忠诚,时刻坚持用党的理论武装头脑、补足精神之钙。习近平总书记曾说:“年轻干部要牢记,坚定理想信念是终身课题,需要常修常炼,要信一辈子,守一辈子。”作为党选出来的青年力量中的一员,我
- 坚定理想信念,锤炼党性修养
知涵知
理想信念是中国共产党人的政治灵魂,是共产党人精神上的“钙”,没有理想信念,理想信念不坚定,精神上就会“缺钙”,就会得“软骨病”。党员干部只有坚定理想信念,强化责任担当,锤炼道德操守,提升党性修养,才能切实做到为党分忧、为国尽责、为民奉献。坚定理想信念,就要强化学习精神、自律精神、担当精神。思想理论上的坚定清醒是政治上坚定的前提,党员干部要始终把理论学习作为政治责任、事业需要和精神追求,积极参加组织
- (扩展)中国剩余定理(模板)
UniverseofHK
数学(扩展)中国剩余定理模板
中国剩余定理:猜数字求解下列同余方程组(模数互质){x≡a1(modm1)x≡a2(modm2)⋮x≡an(modmn)\begin{cases}x\equiva_1\(\mod\m_1\)\\x\equiva_2\(\mod\m_2\)\\\quad\vdots\\x\equiva_n\(\mod\m_n)\end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x≡a1(modm1)x≡a2(modm2)⋮
- 洛谷 P4777 【模板】扩展中国剩余定理(EXCRT)
qq_38232157
noi后缀数组扩展中国剩余定理
1、中国剩余定理(n条同余式子,前提是m[1]~m[n]两两互质)x=r[1](modm[1])x=r[1](modm[2])…x=r[n](modm[n])2、扩展中国剩余定理(n条同余式子,m[1]~m[n]不一定两两互质)x=r[1](modm[1])x=r[1](modm[2])…x=r[n](modm[n])考虑签名两条方程,x=r[1](modm[1]),x=r[1](modm[2])
- 洛谷 P1495 【模板】中国剩余定理(CRT)/曹冲养猪(中国剩余定理)
qq_38232157
洛谷数论
中国剩余定理概念:设m[1],m[2],m[3],…,m[[n]是两两互质的整数。方程组x=a[1](modm[1])//注意,这里的'='表示同余符号x=a[2](modm[2])...x=a[n](modm[n])方程的解x=sum{a[i]*(m/m[i])*t[i]}(1#include#includeusingnamespacestd;constintMaxN=1e5+10;typede
- HDU 1573X问题(扩展中国剩余定理)
数学收藏家
数据结构算法
ProblemDescription求在小于等于N的正整数中有多少个X满足:Xmoda[0]=b[0],Xmoda[1]=b[1],Xmoda[2]=b[2],…,Xmoda[i]=b[i],…(0usingnamespacestd;#defineintlonglong#defineendl'\n'#defineIOSios::sync_with_stdio(false);cin.tie(0);c
- 如何在Java中实现高效的分布式系统:从CAP定理到最终一致性
省赚客app开发者
java开发语言
如何在Java中实现高效的分布式系统:从CAP定理到最终一致性大家好,我是微赚淘客系统3.0的小编,是个冬天不穿秋裤,天冷也要风度的程序猿!今天我们来探讨如何在Java中实现高效的分布式系统,从CAP定理的基础概念到最终一致性的实现策略。一、CAP定理的基础概念CAP定理是分布式系统设计中的基本理论,它指出,在一个分布式系统中,无法同时完全满足一致性(Consistency)、可用性(Availa
- 20天拿到教师资格证
一只吕客
大家好,我们今天来总结小学生心理教育思维导图如下:第一部分:小学生的个体身心发展一、规律:顺序性、阶段性、互补性、不平衡性、差异性二、影响因素:遗传(前提)、成熟、环境、教育、主观能动性(决定作用)三、发展理论:(一)内发论:1.代表人物:孟子、弗洛伊德、格赛尔、威尔逊2.代表思想:人性本善、自然本能(二)外铄论:代表人物:荀子、洛克、华生代表思想:白板说、性恶论(三)多因素论:代表人物:马克思代
- SAP项目管理第二章-方法论实践
syounger
SAP项目管理制造
《SAP项目管理基础与实践》书籍第二章来啦!本章主要是讨论项目管理方法论在实际项目中的实践经验,介绍了SAPActivate中非常有用的文档,并且也探讨了由格力高事件引申的项目质量管理。第二章目录:第2章专题一:SAP项目管理方法论和三角定理2.1项目管理方法论实践2.1.1SAPActivate项目管理方法论路线图2.1.2不同类型项目的方法论实践2.1.3敏捷在SAP项目中的应用2.2三角定理
- 《跳着踢踏舞去上班》书摘和点评
禅堂听雨
跳着踢踏舞去上班卡萝尔·卢米斯这是一本描写巴菲特经历和投资理念的书。有不少经典概念定理。07巴菲特的信(有好的资产也得熬得住,不要跳槽去别的快船,结果发现自己那条慢船突然加速成快艇了)>>格雷厄姆和巴菲特并非在所有问题上都保持一致,但他们共同的观念就是:如果以非常低的价格购进某种资产,假以时日,基本上都能获得回报。08你能跑赢股市吗(节选)(我个人觉得市场大多数时候有效,因为资金是最聪明的。但是乌
- 抽象代数精解【2】
叶绿先锋
基础数学与应用数学抽象代数人工智能
文章目录群消去律的意义消去律与群的其他性质总结难点与例子例子参考文献群下面由文心一言生成群中的消去律是群论中的一个基本定理,它描述了群中元素之间的一种特殊关系。具体来说,群中的消去律包含左右两个方向,可以表述为:左消去律:若(ab=ac)(ab=ac)(ab=ac)且(a,b,c∈G)(a,b,c\inG)(a,b,c∈G)其中(G)是一个群,则b=c。右消去律:若(ba=ca)(ba=ca)(b
- 【机器学习】朴素贝叶斯方法的概率图表示以及贝叶斯统计中的共轭先验方法
Lossya
机器学习概率论人工智能朴素贝叶斯共轭先验
引言朴素贝叶斯方法是一种基于贝叶斯定理的简单概率模型,它假设特征之间相互独立。文章目录引言一、朴素贝叶斯方法的概率图表示1.1节点表示1.2边表示1.3无其他连接1.4总结二、朴素贝叶斯的应用场景2.1文本分类2.2推荐系统2.3医疗诊断2.4欺诈检测2.5情感分析2.6邮件过滤2.7信息检索2.8生物信息学三、朴素贝叶斯的优点四、朴素贝叶斯的局限性4.1特征独立性假设4.2敏感于输入数据的表示4
- 青年干部筑牢理想信念根基
夕阳醉year
习近平总书记指出:“年轻干部接好班,最重要的是接好坚持马克思主义信仰、为共产主义远大理想和中国特色社会主义共同理想而奋斗的班。”“坚定理想信念不是一阵子而是一辈子的事,要常修常炼、常悟常进,无论顺境逆境都坚贞不渝,经得起大浪淘沙的考验。”习近平总书记的重要论述,深刻揭示了理想信念的极端重要性,精辟阐明了年轻干部成长为对党和人民忠诚可靠、堪当时代重任栋梁之才的努力方向和实践路径。坚持理论联系实际。列
- KAN网络技术最全解析——最热KAN能否干掉MLP和Transformer?(收录于GPT-4/ChatGPT技术与产业分析)
u013250861
#LLM/Transformertransformerchatgpt深度学习
KAN网络结构思路来自Kolmogorov-Arnold表示定理。MLP在节点(“神经元”)上具有固定的激活函数,而KAN在边(“权重”)上具有可学习的激活函数。在数据拟合和PDE求解中,较小的KAN可以比较大的MLP获得更好的准确性。相对MLP,KAN也具备更好的可解释性,适合作为数学和物理研究中的辅助模型,帮助发现和寻找更基础的数值规律。(点赞是我们分享的动力)MLP与KAN对比与传统的MLP
- Java 7.1 - 理论 & 算法 & 协议
没有韭菜的饺子
java开发语言
什么是CAP理论?C:Consistency一致性A:Availability可用性P:Partition分区容错性对于理论计算机科学,CAP定理指出,对于一个分布式系统而言,CAP中的三个只能同时满足两个。分区容错性:分布式系统出现网络分区的时候,仍然可以向外提供服务。*网络分区分布式系统中,多个节点之间的网络本来是相连的。但现在因为某些原因,某些节点之间不再连通,网络会被分成多个区域,这就叫网
- 心理学效应系列|取法乎上,得乎其中——吉格勒定理
熙桓心理
吉格勒定理是由美国行为学家J·吉格勒提出的。设定一个高目标就等于达到了目标的一部分。如果从一开始就怀有高远的目标,就会呈现出与众不同的眼界,逐渐形成良好的工作习惯和方法,让每一步都朝着正确的方向前进。气魄大方可成大,起点高才能至高。美国伯利恒钢铁公司的创建者齐瓦勃出生在乡村,所受的教育水平也很低。18岁那年,齐瓦勃到钢铁大王卡内基所属的一个建筑工地打工。一踏进建筑工地,齐瓦勃就抱定了要做同事中最优
- 什么是奈奎斯特采样定理
达西西66
奈奎斯特采样定理
奈奎斯特采样定理,也被称为奈奎斯特定理或奈氏定理,是信号处理领域中至关重要的原理之一。它揭示了在数字信号处理中如何正确地采样模拟信号,以避免信息丢失和混叠现象。本文将深入探讨奈奎斯特采样定理的原理、应用和实例,以及其在通信、音频处理和图像处理等领域的重要性。奈奎斯特采样定理的基本原理奈奎斯特采样定理是由美国工程师哈里·S·奈奎斯特(HarryNyquist)在20世纪20年代提出的。该定理的核心思
- 人工智能与机器学习原理精解【17】
叶绿先锋
基础数学与应用数学人工智能机器学习概率论
文章目录贝叶斯贝叶斯定理的公式推导一、条件概率的定义二、联合概率的分解三、贝叶斯定理的推导四、全概率公式的应用五、总结全概率公式推导一、全概率公式的定义二、全概率公式的推导三、全概率公式的应用贝叶斯定理的原理一、基本原理二、核心概念三、数学表达式四、原理应用五、原理特点朴素贝叶斯定理一、贝叶斯定理基础二、朴素贝叶斯的原理三、朴素贝叶斯的特点朴素贝叶斯公式一、贝叶斯定理二、特征独立性假设三、朴素贝叶
- xml解析
小猪猪08
xml
1、DOM解析的步奏
准备工作:
1.创建DocumentBuilderFactory的对象
2.创建DocumentBuilder对象
3.通过DocumentBuilder对象的parse(String fileName)方法解析xml文件
4.通过Document的getElem
- 每个开发人员都需要了解的一个SQL技巧
brotherlamp
linuxlinux视频linux教程linux自学linux资料
对于数据过滤而言CHECK约束已经算是相当不错了。然而它仍存在一些缺陷,比如说它们是应用到表上面的,但有的时候你可能希望指定一条约束,而它只在特定条件下才生效。
使用SQL标准的WITH CHECK OPTION子句就能完成这点,至少Oracle和SQL Server都实现了这个功能。下面是实现方式:
CREATE TABLE books (
id &
- Quartz——CronTrigger触发器
eksliang
quartzCronTrigger
转载请出自出处:http://eksliang.iteye.com/blog/2208295 一.概述
CronTrigger 能够提供比 SimpleTrigger 更有具体实际意义的调度方案,调度规则基于 Cron 表达式,CronTrigger 支持日历相关的重复时间间隔(比如每月第一个周一执行),而不是简单的周期时间间隔。 二.Cron表达式介绍 1)Cron表达式规则表
Quartz
- Informatica基础
18289753290
InformaticaMonitormanagerworkflowDesigner
1.
1)PowerCenter Designer:设计开发环境,定义源及目标数据结构;设计转换规则,生成ETL映射。
2)Workflow Manager:合理地实现复杂的ETL工作流,基于时间,事件的作业调度
3)Workflow Monitor:监控Workflow和Session运行情况,生成日志和报告
4)Repository Manager:
- linux下为程序创建启动和关闭的的sh文件,scrapyd为例
酷的飞上天空
scrapy
对于一些未提供service管理的程序 每次启动和关闭都要加上全部路径,想到可以做一个简单的启动和关闭控制的文件
下面以scrapy启动server为例,文件名为run.sh:
#端口号,根据此端口号确定PID
PORT=6800
#启动命令所在目录
HOME='/home/jmscra/scrapy/'
#查询出监听了PORT端口
- 人--自私与无私
永夜-极光
今天上毛概课,老师提出一个问题--人是自私的还是无私的,根源是什么?
从客观的角度来看,人有自私的行为,也有无私的
- Ubuntu安装NS-3 环境脚本
随便小屋
ubuntu
将附件下载下来之后解压,将解压后的文件ns3environment.sh复制到下载目录下(其实放在哪里都可以,就是为了和我下面的命令相统一)。输入命令:
sudo ./ns3environment.sh >>result
这样系统就自动安装ns3的环境,运行的结果在result文件中,如果提示
com
- 创业的简单感受
aijuans
创业的简单感受
2009年11月9日我进入a公司实习,2012年4月26日,我离开a公司,开始自己的创业之旅。
今天是2012年5月30日,我忽然很想谈谈自己创业一个月的感受。
当初离开边锋时,我就对自己说:“自己选择的路,就是跪着也要把他走完”,我也做好了心理准备,准备迎接一次次的困难。我这次走出来,不管成败
- 如何经营自己的独立人脉
aoyouzi
如何经营自己的独立人脉
独立人脉不是父母、亲戚的人脉,而是自己主动投入构造的人脉圈。“放长线,钓大鱼”,先行投入才能产生后续产出。 现在几乎做所有的事情都需要人脉。以银行柜员为例,需要拉储户,而其本质就是社会人脉,就是社交!很多人都说,人脉我不行,因为我爸不行、我妈不行、我姨不行、我舅不行……我谁谁谁都不行,怎么能建立人脉?我这里说的人脉,是你的独立人脉。 以一个普通的银行柜员
- JSP基础
百合不是茶
jsp注释隐式对象
1,JSP语句的声明
<%! 声明 %> 声明:这个就是提供java代码声明变量、方法等的场所。
表达式 <%= 表达式 %> 这个相当于赋值,可以在页面上显示表达式的结果,
程序代码段/小型指令 <% 程序代码片段 %>
2,JSP的注释
<!-- -->
- web.xml之session-config、mime-mapping
bijian1013
javaweb.xmlservletsession-configmime-mapping
session-config
1.定义:
<session-config>
<session-timeout>20</session-timeout>
</session-config>
2.作用:用于定义整个WEB站点session的有效期限,单位是分钟。
mime-mapping
1.定义:
<mime-m
- 互联网开放平台(1)
Bill_chen
互联网qq新浪微博百度腾讯
现在各互联网公司都推出了自己的开放平台供用户创造自己的应用,互联网的开放技术欣欣向荣,自己总结如下:
1.淘宝开放平台(TOP)
网址:http://open.taobao.com/
依赖淘宝强大的电子商务数据,将淘宝内部业务数据作为API开放出去,同时将外部ISV的应用引入进来。
目前TOP的三条主线:
TOP访问网站:open.taobao.com
ISV后台:my.open.ta
- 【MongoDB学习笔记九】MongoDB索引
bit1129
mongodb
索引
可以在任意列上建立索引
索引的构造和使用与传统关系型数据库几乎一样,适用于Oracle的索引优化技巧也适用于Mongodb
使用索引可以加快查询,但同时会降低修改,插入等的性能
内嵌文档照样可以建立使用索引
测试数据
var p1 = {
"name":"Jack",
"age&q
- JDBC常用API之外的总结
白糖_
jdbc
做JAVA的人玩JDBC肯定已经很熟练了,像DriverManager、Connection、ResultSet、Statement这些基本类大家肯定很常用啦,我不赘述那些诸如注册JDBC驱动、创建连接、获取数据集的API了,在这我介绍一些写框架时常用的API,大家共同学习吧。
ResultSetMetaData获取ResultSet对象的元数据信息
- apache VelocityEngine使用记录
bozch
VelocityEngine
VelocityEngine是一个模板引擎,能够基于模板生成指定的文件代码。
使用方法如下:
VelocityEngine engine = new VelocityEngine();// 定义模板引擎
Properties properties = new Properties();// 模板引擎属
- 编程之美-快速找出故障机器
bylijinnan
编程之美
package beautyOfCoding;
import java.util.Arrays;
public class TheLostID {
/*编程之美
假设一个机器仅存储一个标号为ID的记录,假设机器总量在10亿以下且ID是小于10亿的整数,假设每份数据保存两个备份,这样就有两个机器存储了同样的数据。
1.假设在某个时间得到一个数据文件ID的列表,是
- 关于Java中redirect与forward的区别
chenbowen00
javaservlet
在Servlet中两种实现:
forward方式:request.getRequestDispatcher(“/somePage.jsp”).forward(request, response);
redirect方式:response.sendRedirect(“/somePage.jsp”);
forward是服务器内部重定向,程序收到请求后重新定向到另一个程序,客户机并不知
- [信号与系统]人体最关键的两个信号节点
comsci
系统
如果把人体看做是一个带生物磁场的导体,那么这个导体有两个很重要的节点,第一个在头部,中医的名称叫做 百汇穴, 另外一个节点在腰部,中医的名称叫做 命门
如果要保护自己的脑部磁场不受到外界有害信号的攻击,最简单的
- oracle 存储过程执行权限
daizj
oracle存储过程权限执行者调用者
在数据库系统中存储过程是必不可少的利器,存储过程是预先编译好的为实现一个复杂功能的一段Sql语句集合。它的优点我就不多说了,说一下我碰到的问题吧。我在项目开发的过程中需要用存储过程来实现一个功能,其中涉及到判断一张表是否已经建立,没有建立就由存储过程来建立这张表。
CREATE OR REPLACE PROCEDURE TestProc
IS
fla
- 为mysql数据库建立索引
dengkane
mysql性能索引
前些时候,一位颇高级的程序员居然问我什么叫做索引,令我感到十分的惊奇,我想这绝不会是沧海一粟,因为有成千上万的开发者(可能大部分是使用MySQL的)都没有受过有关数据库的正规培训,尽管他们都为客户做过一些开发,但却对如何为数据库建立适当的索引所知较少,因此我起了写一篇相关文章的念头。 最普通的情况,是为出现在where子句的字段建一个索引。为方便讲述,我们先建立一个如下的表。
- 学习C语言常见误区 如何看懂一个程序 如何掌握一个程序以及几个小题目示例
dcj3sjt126com
c算法
如果看懂一个程序,分三步
1、流程
2、每个语句的功能
3、试数
如何学习一些小算法的程序
尝试自己去编程解决它,大部分人都自己无法解决
如果解决不了就看答案
关键是把答案看懂,这个是要花很大的精力,也是我们学习的重点
看懂之后尝试自己去修改程序,并且知道修改之后程序的不同输出结果的含义
照着答案去敲
调试错误
- centos6.3安装php5.4报错
dcj3sjt126com
centos6
报错内容如下:
Resolving Dependencies
--> Running transaction check
---> Package php54w.x86_64 0:5.4.38-1.w6 will be installed
--> Processing Dependency: php54w-common(x86-64) = 5.4.38-1.w6 for
- JSONP请求
flyer0126
jsonp
使用jsonp不能发起POST请求。
It is not possible to make a JSONP POST request.
JSONP works by creating a <script> tag that executes Javascript from a different domain; it is not pos
- Spring Security(03)——核心类简介
234390216
Authentication
核心类简介
目录
1.1 Authentication
1.2 SecurityContextHolder
1.3 AuthenticationManager和AuthenticationProvider
1.3.1 &nb
- 在CentOS上部署JAVA服务
java--hhf
javajdkcentosJava服务
本文将介绍如何在CentOS上运行Java Web服务,其中将包括如何搭建JAVA运行环境、如何开启端口号、如何使得服务在命令执行窗口关闭后依旧运行
第一步:卸载旧Linux自带的JDK
①查看本机JDK版本
java -version
结果如下
java version "1.6.0"
- oracle、sqlserver、mysql常用函数对比[to_char、to_number、to_date]
ldzyz007
oraclemysqlSQL Server
oracle &n
- 记Protocol Oriented Programming in Swift of WWDC 2015
ningandjin
protocolWWDC 2015Swift2.0
其实最先朋友让我就这个题目写篇文章的时候,我是拒绝的,因为觉得苹果就是在炒冷饭, 把已经流行了数十年的OOP中的“面向接口编程”还拿来讲,看完整个Session之后呢,虽然还是觉得在炒冷饭,但是毕竟还是加了蛋的,有些东西还是值得说说的。
通常谈到面向接口编程,其主要作用是把系统��设计和具体实现分离开,让系统的每个部分都可以在不影响别的部分的情况下,改变自身的具体实现。接口的设计就反映了系统
- 搭建 CentOS 6 服务器(15) - Keepalived、HAProxy、LVS
rensanning
keepalived
(一)Keepalived
(1)安装
# cd /usr/local/src
# wget http://www.keepalived.org/software/keepalived-1.2.15.tar.gz
# tar zxvf keepalived-1.2.15.tar.gz
# cd keepalived-1.2.15
# ./configure
# make &a
- ORACLE数据库SCN和时间的互相转换
tomcat_oracle
oraclesql
SCN(System Change Number 简称 SCN)是当Oracle数据库更新后,由DBMS自动维护去累积递增的一个数字,可以理解成ORACLE数据库的时间戳,从ORACLE 10G开始,提供了函数可以实现SCN和时间进行相互转换;
用途:在进行数据库的还原和利用数据库的闪回功能时,进行SCN和时间的转换就变的非常必要了;
操作方法: 1、通过dbms_f
- Spring MVC 方法注解拦截器
xp9802
spring mvc
应用场景,在方法级别对本次调用进行鉴权,如api接口中有个用户唯一标示accessToken,对于有accessToken的每次请求可以在方法加一个拦截器,获得本次请求的用户,存放到request或者session域。
python中,之前在python flask中可以使用装饰器来对方法进行预处理,进行权限处理
先看一个实例,使用@access_required拦截:
?