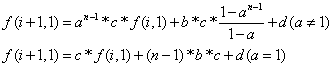BZOJ 3240 [Noi2013] 矩阵游戏 题解

转载请注明：http://blog.csdn.net/jiangshibiao/article/details/24594825

【原题】

3240: [Noi2013]矩阵游戏

Time Limit: 10 Sec   Memory Limit: 256 MB
Submit: 336   Solved: 158
[ Submit][ Status]

Description

婷婷是个喜欢矩阵的小朋友,有一天她想用电脑生成一个巨大的n行m列的矩阵(你不用担心她如何存储)。她生成的这个矩阵满足一个神奇的性质：若用F[i][j]来表示矩阵中第i行第j列的元素，则F[i][j]满足下面的递推式:

F[1][1]=1
F[i,j]=a*F[i][j-1]+b (j!=1)
F[i,1]=c*F[i-1][m]+d (i!=1)
递推式中a,b,c,d都是给定的常数。

现在婷婷想知道F[n][m]的值是多少,请你帮助她。由于最终结果可能很大，你只需要输出F[n][m]除以1,000,000,007的余数。

Input

一行有六个整数n,m,a,b,c,d。意义如题所述

Output

包含一个整数，表示F[n][m]除以1,000,000,007的余数

Sample Input

3 4 1 3 2 6

Sample Output

85

HINT

样例中的矩阵为：

1 4 7 10

26 29 32 35

76 79 82 85

【前言】NOI~~这个我以前一直都瞻仰的名词，竟然能离我这么近~~狠下心来，决定做这题。周围的一圈大神都用各种矩阵乘法秒过，我这种蒟蒻就只好慢慢切了。

虽然公式是自己推的，但是代码实在太复杂了，于是对一个大牛做了一些代码上的参考。

【分析】我们先从简单的来推。考虑第一行。

我们可以根据等比数列推出通项式（纸上划划就行了）

然而这只是第一步。

上述公式其实是建立在f[i][x]上的。

根据f[i][m]和f[i+1][1]的公式，我们可以推出f[i+1][1]和f[i][1]的关系。（其实只要再乘上c，加上d即可）

然后是不是有发现了一个规律？把和a，b，c，d有关的全部当成常数，这个公式可以变成最上面的那个公式！这样，我们可以轻松的求出f[x][1]的值。

之后有两个方法：求出f[n][1]并递推至f[n][m];求出f[n+1][1]后，减去d除以c。

我选了第二种。虽然快了一点，但是还要求逆元。（都做到这种份上了，逆元也不过如此了）

到此为止，就求完了。

【注意】①因为n和m的范围很大，我们要用到费马小定理。

这样，我们可以把n先对（p-1）取模，再计算。（因为除掉的那些乘积是1）

②对于a=1的情况要特判。

【代码】

#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
const ll MaxN=1000010;
const ll MOD=1000000007;
char s[MaxN],t[MaxN];
struct arr{ll uni,ord;}n,m;  //uni表示a=1的情况，ord表示a≠1的情况
ll a,b,c,d,p,k,t;
void give(char *s,arr &n)
{
    int p=strlen(s);
    for (int i=0;i<p;++i)
    {
        n.uni=(n.uni*10+s[i]-48)%MOD;   
        n.ord=(n.ord*10+s[i]-48)%(MOD-1);
    }
}
ll power(ll x,ll y)           //快速幂
{
    ll res=1ll;
    while (y)
    {
      if (y&1ll) res=res*x%MOD;
      y=y/2ll;x=x*x%MOD;
    }
    return res;
}
ll ni(ll x)
{
  return power(x,MOD-2);
}
 
int main()
{
    scanf("%s%s",s,t);
    scanf("%lld%lld%lld%lld",&a,&b,&c,&d);
    give(s,n);give(t,m);
    if (a==1)
    {
        b=((m.uni-1)*b%MOD*c+d)%MOD;
        a=c;
    }
    else
    {
        k=b*ni(a-1)%MOD;                       //第一次推
        t=power(a,m.ord-1);
        a=c*t%MOD;
        b=((t-1)*k%MOD*c+d)%MOD;
    }
    if (a==1)
    {
        p=(1+n.uni*b)%MOD;
    }
    else
    {
        k=b*ni(a-1)%MOD;
        t=power(a,n.ord);
        p=(t+(t-1)*k)%MOD;                     //第二次推
    }
    printf("%lld",((p-d)*ni(c)%MOD+MOD)%MOD);  //逆元部分
    return 0;
}