hdu5651（乘法逆元&&组合数）

题意：xiaoxin巨从小就喜欢字符串，六年级的时候他就知道了什么是回文串。这时，xiaoxin巨说到：如果一个字符串 SSS 是回文串，那么该字符串从前往后看和从后往前看是一样一样的。
六年级的暑假，xiaoxin很快就做完了暑假作业，然后到腾讯做起了实习生。这日，leader给了xiaoxin一个字符串，请xiaoxin帮忙写一个函数来生成所有可能的回文串，可以任意改变字符串的顺序但是不可以扔掉某个字符。并且leader告诉xiaoxin，每生成一个不一样的回文串就可以得到一颗西瓜糖。

请你帮忙计算xiaoxin的leader最多需要买多少颗西瓜糖呢

分析：回文串，只可能有一个字母的个数为奇数，所以有两个及两个以上的奇数个字母的情况直接输出0。先统计各个字母的个数，然后只需要求解一般的个数就行了，因为另一半是对称的。所以要算出每个字母个数一半的不想异的全排列就好了；求解的时候要求到除法取模问题，只需求解除数的逆元。

不想异的全排列公式 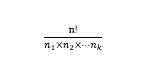  一共有n个数，k种，每种ni个球求全排列个数

逆元的求解方法  ：求解n对于m的逆元只需求(n*x)%m=1。用扩展欧几里得来求解

扩展欧几里得算法如下：http://blog.csdn.net/qq_27599517/article/details/50888092

代码如下：

#include <set>
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <vector>
#include <string>
#include <utility>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <functional>

using namespace std;
long long gcd(long long a,long long mod,long long& x, long long& y){
    if(!mod){
        x=1;
        y=0;
        return a;
    }
    long long ans=gcd(mod,a%mod,x,y);
    long long t=x;
    x=y;
    y=t-a/mod*y;
    return ans;
}//求解逆元
const long long mod=1000000007;
long long a[30];
long long su(long long sum){
    long long ans=1;
    for(long long i=2;i<=sum;i++)
    ans=ans*i%mod;
    return ans;
}//求解sum的阶乘
int main(){
    long long t;
    scanf("%I64d",&t);
    while(t--){
        memset(a,0,sizeof(a));
        char s[1050];
        scanf("%s",s);
        long long len=strlen(s);
        for(long long i=0;i<len;i++){
            a[s[i]-'a']++;
        }
        long long flag=0;
        for(long long i=0;i<26;i++){
            if(a[i]&1)flag++;
        }
        if(flag>1){
            puts("0");
            continue;
        }
        long long sum=0;
        long long x,y;
        for(long long i=0;i<26;i++){
            a[i]/=2;
            sum+=a[i];
            if(a[i]!=0){
                a[i]=su(a[i]);
                gcd(a[i],mod,x,y);
                if(x<0)x+=mod;
                a[i]=x;
            }
        }
        long long ans=1;
        for(long long i=2;i<=sum;i++)
        ans=ans*i%mod;
        for(long long i=0;i<26;i++){
            if(a[i]!=0)
            ans=ans*a[i]%mod;
        }
        printf("%I64d\n",ans%mod);
    }
    return 0;
}