二分图系列•二分图判定•匈牙利算法二分图的最大匹配•二分图最小点覆盖及最大独立集
二分图一•二分图判定
描述
大家好,我是小Hi和小Ho的小伙伴Nettle,从这个星期开始由我来完成我们的Weekly。
新年回家,又到了一年一度大龄剩男剩女的相亲时间。Nettle去姑姑家玩的时候看到了一张姑姑写的相亲情况表,上面都是姑姑介绍相亲的剩男剩女们。每行有2个名字,表示这两个人有一场相亲。由于姑姑年龄比较大了记性不是太好,加上相亲的人很多,所以姑姑一时也想不起来其中有些人的性别。因此她拜托我检查一下相亲表里面有没有错误的记录,即是否把两个同性安排了相亲。
OK,让我们愉快的暴力搜索吧!
才怪咧。
对于拿到的相亲情况表,我们不妨将其转化成一个图。将每一个人作为一个点(编号1..N),若两个人之间有一场相亲,则在对应的点之间连接一条无向边。(如下图)

因为相亲总是在男女之间进行的,所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色,女性的节点染色黑色。对于得到的无向图来说,即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色,则表示这一条边所表示的记录有误。
由于我们并不知道每个人的性别,我们的问题就转化为判定是否存在一个合理的染色方案,使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。
那么,我们不妨将所有的点初始为未染色的状态。随机选择一个点,将其染成白色。再以它为起点,将所有相邻的点染成黑色。再以这些黑色的点为起点,将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图)
在染色的过程中,我们应该怎样发现错误的记录呢?相信你一定发现了吧。对于一个已经染色的点,如果存在一个与它相邻的已染色点和它的颜色相同,那么就一定存在一条错误的记录。(如上图的4,5节点)
到此我们就得到了整个图的算法:
- 选取一个未染色的点u进行染色
- 遍历u的相邻节点v:若v未染色,则染色成与u不同的颜色,并对v重复第2步;若v已经染色,如果 u和v颜色相同,判定不可行退出遍历。
- 若所有节点均已染色,则判定可行。
#include<iostream>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;
int N,M,book[10005];
void Check()
{
queue<int> que;
memset(book,0,sizeof(book));
vector<int> node[N+2]; // vector[] 下标从0开始, 顶点从1开始编号,因此数组维数至少要比顶点总数大1
int u,v;
for(int i=1;i<=M;++i)
{
cin>>u>>v;
node[u].push_back(v);
node[v].push_back(u);
}
for(int k=1;k<=N;++k)
{
int flag=1;
if(book[k]==0)
{
book[k]=1;
que.push(k);
while(!que.empty()) // Floodfill 把相邻的顶点染成相反的颜色,1->-1 / -1->1
{
int tmp=que.front();// cout<<"("<<tmp<<","<<book[tmp]<<")"<<endl;
que.pop();
for(vector<int>::iterator iter=node[tmp].begin();iter!=node[tmp].end();++iter)
{
if(book[tmp]!=book[(*iter)])
{
if(book[(*iter)]==0)
{
book[(*iter)]=-book[tmp];
que.push((*iter));
}
}
else
{
cout<<"Wrong"<<endl;
return ;
}
}
}
}
}
cout<<"Correct"<<endl;
return ;
}
int main()
{
ios::sync_with_stdio(false);
int T;
cin>>T;
while(T>0)
{
T--;
cin>>N>>M;
Check();
}
return 0;
}
二分图二•二分图最大匹配之匈牙利算法
描述
上一回我们已经将所有有问题的相亲情况表剔除了,那么接下来要做的就是安排相亲了。因为过年时间并不是很长,所以姑姑希望能够尽可能在一天安排比较多的相亲。由于一个人同一天只能和一个人相亲,所以要从当前的相亲情况表里选择尽可能多的组合,且每个人不会出现两次。不知道有没有什么好办法,对于当前给定的相亲情况表,能够算出最多能同时安排多少组相亲呢?
同样的,我们先将给定的情况表转换成图G=(V,E)。在上一回中我们已经知道这个图可以被染成黑白两色。不妨将所有表示女性的节点记为点集A,表示男性的节点记为点集B。则有A∪B=V。由问题可知所有边e的两个端点分别属于AB两个集合。则可以表示成如下的图:
同样的,我们将所有的边分为两个集合。集合S和集合M,同样有S∪M=E。边集S表示在这一轮相亲会中将要进行的相亲,边集M表示在不在这一次进行。对于任意边(u,v) ∈ S,我们称u和v为一组匹配,它们之间相互匹配。在图G,我们将边集S用实线表示,边集M用虚线表示。得到下图:
则原问题转化为,最多能选择多少条边到集合S,使得S集合中任何两条边不相邻(即有共同的顶点)。显然的,|S|<=Min{|A|, |B|}。
那么能不能找到一个算法,使得能够很容易计算出尽可能多的边能够放入集合S?我们不妨来看一个例子:
对于已经匹配的点我们先不考虑,我们从未匹配的点来做。这里我们选择A集合中尚未匹配的点(A3和A4)考虑:
对于A3点,我们可以发现A3与B4右边相连,且都未匹配。则直接将(A3,B4)边加入集合S即可。
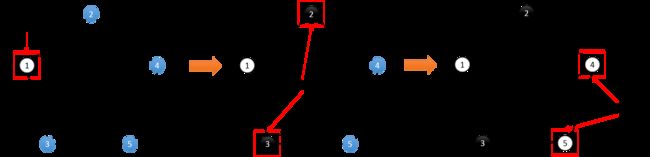
对于A4点,我们发现和A4相连的B3,B4点都已经匹配了。但是再观察可以发现,如果我们将A2和B2相连,则可以将B3点空出来。那么就可以同时将(A2,B2),(A4,B3)相连。将原来的一个匹配变成了两个匹配。
让我们来仔细看看这一步:我们将这次变换中相关联的边标记出来,如下图所示紫色的3条边(A2,B2),(A2,B3),(A4,B3)。
这三条边构成了一条路径,可以发现这条路径有个非常特殊的性质。虚线和实线相互交错,并且起点和终点都是尚未匹配的点,且属于两个不同的集合。我们称这样的路径为交错路径。
再进一步分析,对于任意一条交错路径,虚线的数量一定比实线的数量多1。我们将虚线和实线交换一下,就变成了下面的图:
在原来1个匹配的基础上,我们得到了2个新的匹配,S集合边的数量也增加了1。并且原来在已经匹配的点仍然是已经匹配的状态。
再回头看看A3点匹配时的情况:对于(A3,B4)这一条路径,同样满足了交错路径的性质。
至此我们得到了一个找新匹配的有效算法:
选取一个未匹配的点,查找是否存在一条以它为起点的交错路径。若存在,将该交错路径的边虚实交换。否则在当前的情况下,该点找不到可以匹配的点。
又有对于已经匹配的点,该算法并不会改变一个点的匹配状态。所以当我们对所有未匹配的点都计算过后,仍然没有交错路径,则不可能找到更多的匹配。此时S集合中的边数即为最大边数,我们称为最大匹配数。
那么我们再一次梳理整个算法:
1. 依次枚举每一个点i;
2. 若点i尚未匹配,则以此点为起点查询一次交错路径。
最后即可得到最大匹配数。
在这个基础上仍然有两个可以优化的地方:
1.对于点的枚举:当我们枚举了所有A中的点后,无需再枚举B中的点,就已经得到了最大匹配。
2.在查询交错路径的过程中,有可能出现Ai与Bj直接相连,其中Bj为已经匹配的点,且Bj之后找不到交错路径。之后又通过Ai查找到了一条交错路径{Ai,Bx,Ay,…,Az,Bj}延伸到Bj。由于之前已经计算过Bj没有交错路径,若此时再计算一次就有了额外的冗余。所以我们需要枚举每个Ai时记录B集合中的点是否已经查询过,起点不同时需要清空记录。使用book[i]标记寻找增广路的过程中,顶点i是否已经查询过即可避免不必要的过程。
Function FindPath(u)
For v∈u的相邻节点
If v没有被标记过已经查询
标记v已经查询过
If v未匹配 or FindPath(v的匹配的点) Then
更改u的匹配为v
Return Ture
End If
End For
Return False
/*主调函数*/
For i ∈ V
清空查询标记
If FindPath(i) Then
匹配计数+1
End If
#include<iostream>
#include<cstring>
using namespace std;
int e[1005][1005],match[1005],book[1005],N,M;
bool DFS(int pos)
{
book[pos]=1;
for(int i=1;i<=N;++i)
{
if(e[pos][i]&&!book[i])
{
book[i]=1;
if(match[i]==0||DFS(match[i])) // 如果i已经被匹配了,则看与i匹配的另一顶点match[i]能否再找到匹配
{
match[pos]=i; // i没有匹配或者与i的匹配的另一顶点已找到其它新的匹配,则增广路成功,登记信息
match[i]=pos;
return true;
}
}
}
return false;
}
int main()
{
ios::sync_with_stdio(false);
cin>>N>>M;
for(int i=1;i<=M;++i)
{
int u,v;
cin>>u>>v;
e[u][v]=e[v][u]=1;
}
int tot=0;
for(int t=1;t<=N;++t)
{
if(match[t]==0)
{
memset(book,0,sizeof(book));
if(DFS(t)) tot++;
}
}
cout<<tot<<endl;
return 0;
}
二分图三·二分图最小点覆盖和最大独立集
描述
在上次安排完相亲之后又过了挺长时间,大家好像都差不多见过面了。不过相亲这个事不是说那么容易的,所以Nettle的姑姑打算收集一下之前的情况并再安排一次相亲。所以现在摆在Nettle面前的有2个问题:
1.姑姑想要了解之前所有相亲的情况。对于任一个一次相亲,只要跟参与相亲的两人交流就可以得到这次相亲的情况。如果一个人参加了多次相亲,那么跟他交流就可以知道这几次相亲的情况。那么问题来了,挖掘技术到底哪家强姑姑最少需要跟多少人进行交流可以了解到所有相亲的情况。(二分图最小点覆盖->最少的点覆盖所有边)
问题1解答
2.因为春节快要结束了,姑姑打算给这些人再安排一次集体相亲。集体相亲也就是所有人在一起相亲,不再安排一对一对的进行相亲。但是姑姑有个条件,要求所有参与相亲的人之前都没有见过。也就是说在之前的每一次相亲中的两人不会被同时邀请来参加这次集体相亲。那么问题又来了,姑姑最多可以让多少人参与这个集体相亲。
问题2解答
问题1.二分图最小点覆盖问题
在图G中选取尽可能少的点,使得图中每一条边至少有一个端点被选中。
这个问题在二分图问题中被称为最小点覆盖问题。即用最少的点去覆盖所有的边。
结论:由König定理可知最小点覆盖的点数 = 二分图最大匹配
König定理,二分图最小点覆盖 = 二分图最大匹配数
二分图最大匹配的König定理及其证明
本文将是这一系列里最短的一篇,因为我只打算把König定理证了,其它的废话一概没有。
以下五个问题我可能会在以后的文章里说,如果你现在很想知道的话,网上去找找答案:
1. 什么是二分图;
2. 什么是二分图的匹配;
3. 什么是匈牙利算法;
4. König定理证到了有什么用;
5. 为什么o上面有两个点。
König定理是一个二分图中很重要的定理,它的意思是,一个二分图中的最大匹配数等于这个图中的最小点覆盖数。如果你还不知道什么是最小点覆盖,我也在这里说一下:假如选了一个点就相当于覆盖了以它为端点的所有边,你需要选择最少的点来覆盖所有的边。比如,下面这个图中的最大匹配和最小点覆盖已分别用蓝色和红色标注。它们都等于3。这个定理相信大多数人都知道,但是网络上给出的证明并不多见。有一些网上常见的“证明”明显是错误的。因此,我在这里写一下这个定理的证明,希望对大家有所帮助。
假如我们已经通过匈牙利算法求出了最大匹配(假设它等于M),下面给出的方法可以告诉我们,选哪M个点可以覆盖所有的边。
匈牙利算法需要我们从右边的某个没有匹配的点,走出一条使得“一条没被匹配、一条已经匹配过,再下一条又没匹配这样交替地出现”的路(交错轨,增广路)。但是,现在我们已经找到了最大匹配,已经不存在这样的路了。换句话说,我们能寻找到很多可能的增广路,但最后都以找不到“终点是还没有匹配过的点”而失败。我们给所有这样的点打上记号:从右边的所有没有匹配过的点出发,按照增广路的“交替出现”的要求可以走到的所有点(最后走出的路径是很多条不完整的增广路)。那么这些点组成了最小覆盖点集:右边所有没有打上记号的点,加上左边已经有记号的点。看图,右图中展示了两条这样的路径,标记了一共6个点(用 “√”表示)。那么,用红色圈起来的三个点就是我们的最小覆盖点集。
首先,为什么这样得到的点集点的个数恰好有M个呢?答案很简单,因为每个点都是某个匹配边的其中一个端点。如果右边的哪个点是没有匹配过的,那么它早就当成起点(独立集寻找的起点)被标记了;如果左边的哪个点是没有匹配过的,那就走不到它那里去(否则就找到了一条完整的增广路)。而一个匹配边又不可能左端点是标记了的,同时右端点是没标记的(不然的话右边的点就可以经过这条边到达了)。因此,最后我们圈起来的点与匹配边一一对应。
其次,为什么这样得到的点集可以覆盖所有的边呢?答案同样简单。不可能存在某一条边,它的左端点是没有标记的,而右端点是有标记的。原因如下:如果这条边不属于我们的匹配边,那么左端点就可以通过这条边到达(从而得到标记);如果这条边属于我们的匹配边,那么右端点不可能是一条路径的起点,于是它的标记只能是从这条边的左端点过来的(想想匹配的定义),左端点就应该有标记。
最后,为什么这是最小的点覆盖集呢?这当然是最小的,不可能有比M还小的点覆盖集了,因为要覆盖这M条匹配边至少就需要M个点(再次回到匹配的定义)。
问题2.二分图最大独立集
依旧转化为图G=(V,E),则问题转化为:
在图G中选取尽可能多的点,使得任意两个点之间没有连边。
这个问题在二分图问题中被称为最大独立集问题。
结论:最大独立集的点数 = 总点数 - 二分图最大匹配,(实际上出去最小独立集顶点,剩下就是一个最大匹配)
假设最大独立集的点数为|U|,二分图最大匹配的匹配数为|M|,最大匹配中所有顶点集合为EM
先证明 |U|≤|V|-|M|
M中任意一条边的两个端点是连接的,所有对于M中的边必有一个端点不在|U|集合中,所以|M|≤|V|-|U|
再证明|U|≥|V|-|M|
首先我们知道一定有|U|≥|V|-|EM|,即将最大匹配的点删除之后,剩下的点一定都不相连。
接下来我们考虑能否将M集合中的一个端点放入U中:
假设(x,y)属于M,存在(a,x),(b,y),且a,b都在U中,则会出现两种情况:
故有a,b两点中至多只有1个点属于U,则我们总是可以选取x,y中一个点放入集合U,所以|U|≥|V|-|EM|+|M|=|V|-|M|
综上有|U|=|V|-|M|