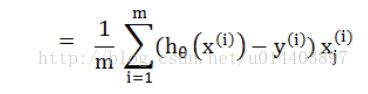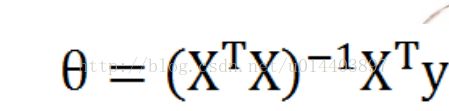梯度下降算法

注：本文所有图片及文章架构均来源于“算法团子”，后经本人改写所成

以上两幅图片显然左侧这幅能更好描述房价与面积关系，但怎样用数学表示？

我们将其误差定义为J，所有点的欧氏距离之和其实就是它的误差J

J=all（y-h(x)）

如感知器算法，我们的目标就是减小J，根据梯度下降含义，我们可以将J沿着下降最快的方向调整权值，使其能够收敛到J的最小值（极值）

下降最快的方向，就是一阶导数的反方向

如下图所示：

问题：

1.w的初始值会影响结果吗？

答：看情况，若只有一个极小值点那不影响，若不是，则会有影响（这也是梯度下降算法的局限性之一～）

2.一定能找到最优解么？

答：同于上一问，不一定

3.当初始的时候，就已经为局部最优解了，w怎样变化？

答：如公式所示，导数为0，不会再变化了

4.循环结束条件是什么？

答；收敛或接近收敛，也可以自己定义一个循环次数以控制执行时间

5.a的取值

5.1 a需要不断变化么，以缩小学习速率？

答：不需要，因为导数会越来越小的～

5.2 a初始值取得过大会怎样？

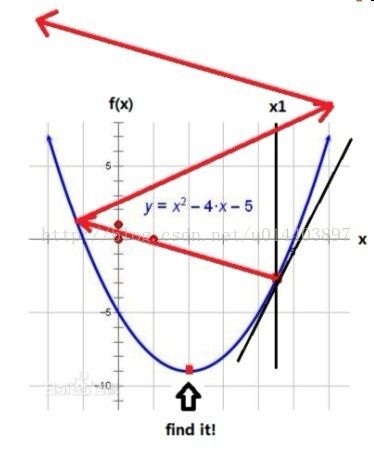
a的值取得过大会导致无法收敛的情况发生，当其太大，可能会使生成的新点的导数比原来点的更大，以至于无限循环下去如下图：

5.3 a初始值过小会怎样

答：学习效率太慢，导致训练好久都没有收敛

J的推导：

J的推导过程略，此处仅写出第一步和结果，有兴趣可以自己慢慢推～

（注意，化简时候一定注意符号问题）

注：i代表训练样本中的第几个样本

w=w-J‘（w）    注就是减去上方那一坨

C语言代码如下：（使用之前需要特征归一化，关于特诊归一化见下一篇博文）

//偏导数计算的实现：
double comput_gradient(double x[][],int y[],int w[],int feature_num,int sample_num,int pian){
    //pian 变量代表着你要对哪一个求偏导数，哪一个w求
    doub  sum=0;
    for(int i=0;i<sample_num;i++){
        double tem=0;
        for(int j=0;j<feature_num;j++){
            tem+=x[i][j]*y[j];
        }
        sum+=(tem-y[i])*x[i]pian]
    }
    return sum/sample_num;
}
//以下是梯度下降算法的实现

<pre name="code" class="cpp">void gradient(double x[][],double y[],double a,double w[],int feature_num,int sample_num,int iteratortime){
    while(iteratortime--){
        double* tem=new double[feature_num];
        for(int i=0;i<feature_num;i++){
            tem[i]=w[i]-]-a*comput_gradient(x,y,w,feature_num,sample_num,i);
        }
        for(int i=0;i<feature_num;i++)
            w[i]=tem[i];
    }
}

最小二程法：

最小二乘法与梯度下降其实不是同一种算法

最小二乘法其实是对每个w求偏导，联立方程解出的，也叫标准方程法，具体为：

二者区别：梯度下降          最小二乘

                        有a                  无a

                  需迭代                不用迭代

               样本大无所谓               矩阵计算复杂度高（规模小）