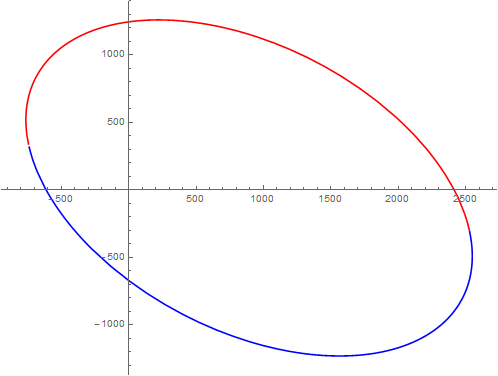
某个偏锥面跟平面的交线

问题

圆锥曲线在射影几何里最原始的定义是:

圆锥曲线（英语：conic section），又称圆锥截痕、圆锥截面、二次平面曲线，是数学、几何学中通过平切圆锥（严格为一个正圆锥面和一个平面完整相切）得到的曲线，包括圆，椭圆，抛物线，双曲线及一些退化类型。

圆锥曲线在约公元前200年时就已被命名和研究了，其发现者为古希腊的数学家阿波罗尼奥斯，那时阿波罗尼阿斯对它们的性质已做了系统性的研究。

圆锥曲线应用最广泛的定义为（椭圆，抛物线，双曲线的统一定义）：动点到一定点（焦点）的距离与其到一定直线（准线）的距离之比为常数（离心率e）的点的集合是圆锥曲线。对于0 < e < 1得到椭圆，对于e = 1得到抛物线，对于e > 1得到双曲线。

在笛卡尔坐标系内，二元二次方程的图像可以表示圆锥曲线，并且所有圆锥曲线都以这种方式引出。方程有如下形式

Ax2+Bxy+Cy2+Dx+Ey+F=0 ; 有着参数 A ,， B ,和 C ,不得皆等于0,。

如果 B2−4AC<0 ,，方程表示椭圆（除非圆锥曲线退化了，例如 x2+y2+10=0 ）；
如果 A=C 且 B=0 ,且 D2+E2−4F>0 ,,方程表示圆；
如果 B2−4AC=0 ,，方程表示抛物线；
如果 B2−4AC>0 ,，方程表示双曲线；
如果还有 A=−C ,，方程表示直角双曲线。

Wolfram mathworld里面是:

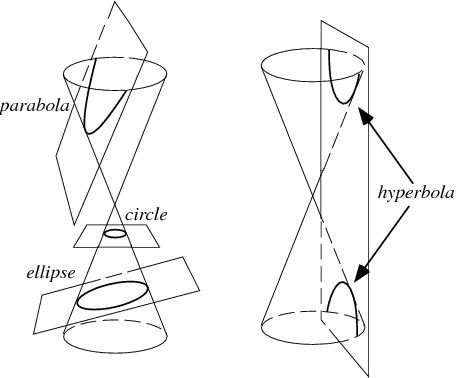
The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone. For a plane perpendicular to the axis of the cone, a circle is produced. For a plane that is not perpendicular to the axis and that intersects only a single nappe, the curve produced is either an ellipse or a parabola (Hilbert and Cohn-Vossen 1999, p. 8). The curve produced by a plane intersecting both nappes is a hyperbola (Hilbert and Cohn-Vossen 1999, pp. 8-9).

The ellipse and hyperbola are known as central conics.

Because of this simple geometric interpretation, the conic sections were studied by the Greeks long before their application to inverse square law orbits was known. Apollonius wrote the classic ancient work on the subject entitled On Conics. Kepler was the first to notice that planetary orbits were ellipses, and Newton was then able to derive the shape of orbits mathematically using calculus, under the assumption that gravitational force goes as the inverse square of distance. Depending on the energy of the orbiting body, orbit shapes that are any of the four types of conic sections are possible.

A conic section may more formally be defined as the locus of a point P that moves in the plane of a fixed point F called the focus and a fixed line d called the conic section directrix (with F not on d ) such that the ratio of the distance of P from F to its distance from d is a constant e called the eccentricity. If e=0 , the conic is a circle, if 0<e<1 , the conic is an ellipse, if e=1 , the conic is a parabola, and if e>1 , it is a hyperbola.

上面的维基里和mathworld的描述主要基于正圆锥,我是指,锥面的奇点(顶点)向底面(所谓底面,是直截圆锥面得到圆的任意平面)正投影正好在底面圆心的类型.

底面是圆，但锥面顶点向底面正投影偏离底面圆心的偏圆锥(如下图)，或者, 锥面顶点向截锥面不是圆而是”椭圆”的平面正投影之后落在椭圆的中心的扁圆锥(如下图)——它们本质是差不多一回事——则用平面截锥面得到的非退化交线是不是还是二次曲线？

结论

这样的说法也适用于偏圆锥或扁圆锥(顶点正投影到椭圆底面中心的情形)。

举例说明

证明是繁琐的【除非用中心投影法】。

证明的思路大致是这样的，前面提到的圆锥面，不论偏（或扁）还是正房，都有一个平面(就是圆锥的底面所在的平面)截它是二次曲线(记为 c )；任意其它平面截该锥面得到的交线 c′ 都相当于对 c 作一个中心投影。如果用平面曲线的实对称二次型 C3×3 来表示,记作 c≈C ，那么中心投影的变换总可以用一个平面的满秩的单应 H 表示，从而 c′≈HTCH 也是一个实对称二次型，必然对应于一条二次曲线。

估计射影几何或投影几何的优越性就这么来的：很复杂的解析的问题能够被简化。

不知道原始的文献如何定义了圆锥曲线并得到二次曲线形式的方程。

举一个特定的例子看看其繁琐性的同时，也验证下前面的结论。

考虑下面的锥面:

⎧⎩⎨⎪⎪x=y=z=3ucosv+3(1−u)3usinv+3(1−u)5(1−u)

其隐函数形式:

F(x,y,z)=(5x−3z)2+(5y−3z)2−9(5−z)2

任意取一个平面跟它相交, 比如：

9x+2y+3z−10=0

求解关于 x,y 的二元二次方程组:

{(5x−3z)2+(5y−3z)2−9(5−z)29x+2y+3z−10=0=0

得到3维交线的参数方程(参数为 z ), 两个解合并起来是一条空间曲线:

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x1=y1=z1=1425(−177z∓219−−√−81z2−150z+875−−−−−−−−−−−−−−−−√+450)1425(159z±919−−√−81z2−150z+875−−−−−−−−−−−−−−−−√+100)z

把空间曲线向截平面 9x+2y+3z−10=0 作正投影,再作一个把该截平面反射到 xoy 坐标平面上的反射,就能得到该空间曲线的平面曲线形式:

它的参数方程刚好能改写成关于 x,y 的二次隐函数形式(但是式子的系数看上去比较复杂)