暴力搜索------回溯法
回溯法(backtracking)是深度优先搜索(DFS)的一种,按照深度优先的顺序便利解答树。应用范围很广,只要能把待求解的问题分成不太多的步骤,每个步骤又只有不太多的选择,都可以考虑应用回溯法。在学习回溯法之前,一定要保证递归程序能熟练准确地写出。
当把问题分成若干步骤并递归求解时,如果当前步骤没有合法选择则函数将返回上一级递归调用。
例如:
八皇后问题:在棋盘上放置八个皇后,使得它们互不攻击,每个皇后的攻击范围是同行同列同对角线,找出所有解的个数。
如果把问题相成从64个格子中选8个格子,那么根据组合数学需要4.426*10^9种方案,但是如果用数组C[x]表示第x行皇后的列编号,则问题变成了全排列生成问题。而0~7的全排列一共有8!=40320个,枚举量不会超过它 。
下面以四皇后问题阐述具体思路:
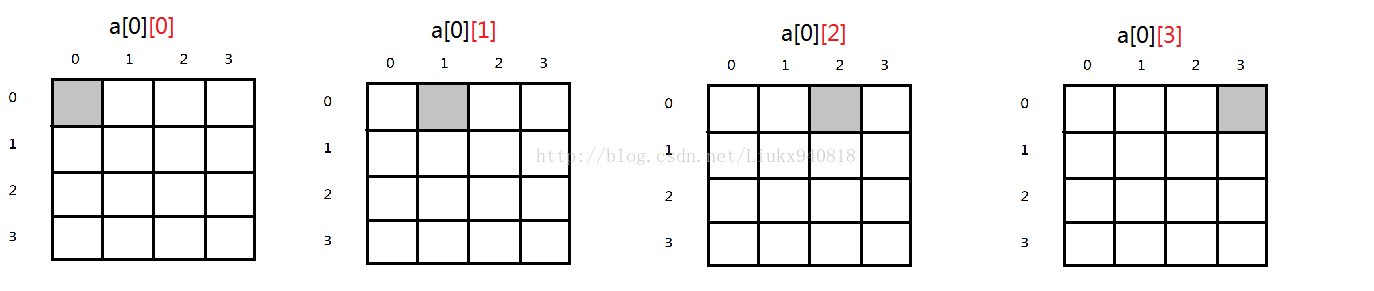
在第一行,皇后可以在第一列、第二列、第三列、第四列。用a[i][j]来表示皇后可能放置的位置,如图
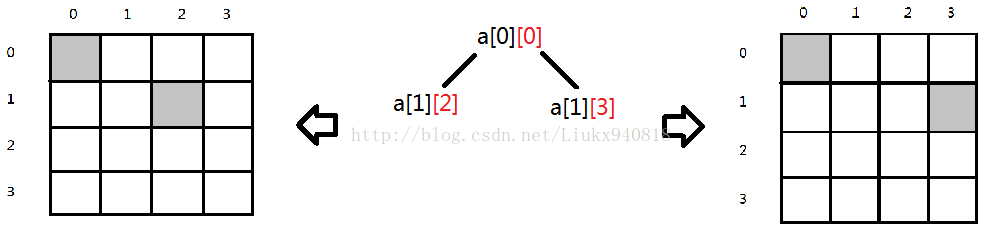
假设第一行的皇后在a[0][0],那么在第二行皇后可能放置的合法位置如图
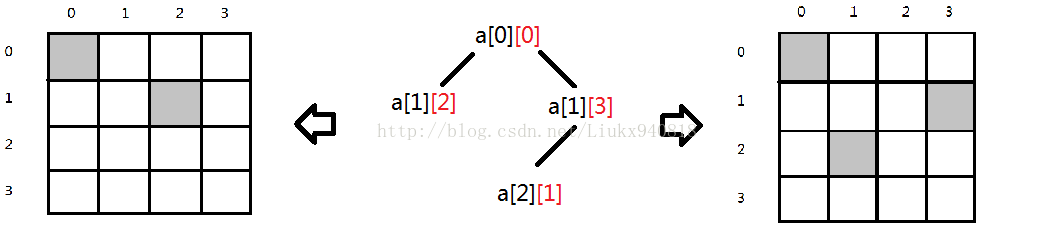
假设第二行皇后放在a[1][2],那么第三行无法放皇后,所以回溯到第一行的a[0][0],走下一条路a[1][3],如图
第四行无法再放置皇后,说明第一个皇后不能在a[0][0],回溯到最开始,让皇后放置在a[0][1],依此类推得到解答树。
观察解答树,改变一次行,遍历四个列(a[1][0]和a[1][1]的情况由于不放置皇后所以没有画在图上,但是这两种情况的否定需要遍历判断),所以只需要用一个一维数组C[x]来表示第x行皇后的列编号即可。代码如下:
需要在主函数中读入n(n*n的棋盘),并将解的个数tot清零,然后调用Dfs(0),即可求得解。
void Dfs(int cur) //cur表示行
{
if(cur == n) //递归边界,每走到此得到一个解
tot++; //tot表示解的个数
else
{
for(int i = 0; i < n; i++) //i表示列
{
int ok = 1; //判断能否放皇后的标志
C[cur] = i; //尝试把第cur行的皇后放在第i列
for(int j = 0; j < cur; j++) //j表示行,通过检查前面几行判断能否放皇后
{
/*判断列、主对角线、副对角线与前几行皇后是否冲突*/
if(C[cur]==C[j]||cur-C[cur]==j-C[j]||cur+C[cur]==j+C[j])
{
ok = 0;
break;
}
}
if(ok)
Dfs(cur + 1);
}
}
}
C[cur] == C[j] 、cur - C[cur] == j - C[j]、cur + C[cur] == j + C[j]的理解如下:
由于是逐行放置,所以横向一定不会冲突,只需检查是否纵向和斜向冲突即可,在直角坐标系中,y = -x与y = x为正斜向线,类比坐标系,cur为行,抽象为横坐标,C[cur]为列,抽象为纵坐标,由于不一定要通过原点,所以y-x与y+x可以为任意常数,只要这个常数与前一行相等,说明两皇后斜向冲突。