二分图（三）——KM算法

写完这一章，大概二分图的匹配问题也该完结了吧。
其实我自己现在对KM算法也是刚刚理解，有理解不到位之处还请大家指出。
KM算法：求在一个二分图的完备匹配中的最大权值匹配的算法。（下文简称为最佳完备匹配）
似乎跟匈牙利算法有点相似，
所以我们要引入一个基于匈牙利算法的一种算法，叫做KM算法。
步骤如下：
首先用邻接矩阵存储二分图，注意：如果只想求最大权值匹配而不要求是完备匹配的话，请把各个不相连的边的权值设置为0。
之后进行下述步骤：
1.运用贪心算法初始化标杆。
2.运用匈牙利算法找到完备匹配。
3.如果找不到，则通过修改标杆，增加一些边。
4.重复2，3的步骤，找到完备匹配时可结束。
不得不说整个博文时间跨度到了一天……
继续写……
标杆分为X标杆和Y标杆，一般我们把比较少的点放在X标杆一侧。
这样进行算法：
首先要初始化两个标杆分别为X标杆和Y标杆，X标杆初始化为与之相连的最大边权，Y标杆初始化为0，且直接加入拥有最大边权的边。如果发现此时的匹配就是完备匹配，那么直接退出，否则进行标杆的更改。从第一个节点开始扫描，如果有合法的增广路，那么将其反选，扩充路径，如果该节点没有合法的增广路，那么则将增广路上的所有的X标杆上的点加入点集S,将Y标杆上的所有点加入点集T，从S和不在T集合中的点里面，计算d=min{L(x)+L(y)-w(x,y)};计算后，将在S点集内的x的顶标减d，在T的y的顶标加d。并将目前没有加入二分图的权值和等于顶标和的边作为未匹配边加入到二分图中，然后再在该节点寻找增广路，如果还是没有，则再次通过更改标杆来增加边，直到有增广路出现为止。之后重复寻找增广路的步骤以及更改标杆的步骤，如果出现了完备匹配，那么直接退出。
我认为：求d的过程是把xy的顶标和及其权值相差最小的边加入到二分图中，而修改顶标的过程是使得其顶标之和等于新增入的边权，并使得之前选择的那些边仍然存在（即其顶标和仍等于权值和）。
看得有点绕？
我们来看一下强行手工模拟：
有邻接矩阵如下：
x1 x2 x3 x4 x5
y1 7 3 14 19 23
y2 8 10 15 18 20
y3 6 8 12 16 19
y4 4 9 13 20 25
y5 2 7 12 10 15
非常完美的一个邻接矩阵，其中斜体为边权最大值。下面我们按照上面的晕乎乎的步骤来进行模拟吧。
初始化标杆使X标杆的值为斜体字的值。

连接每条边并且使得x1和y3匹配，然后遍历x2，发现x2找不到合法增广路。

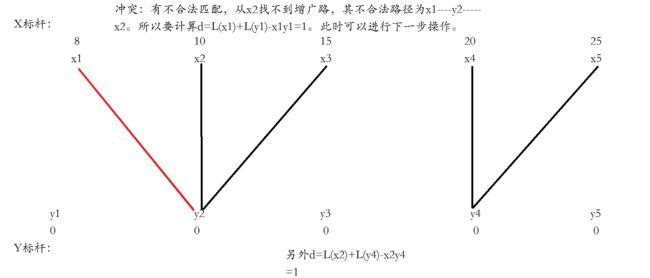
把不合法路径上的x点都归为点集S,y点都归为T,将不在T中的y点和在S中的点尝试进行加边。

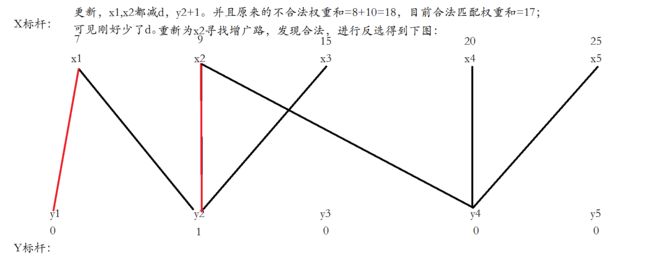
找到两条边，更新顶标之后，成功形成增广路，运用匈牙利算法反选。

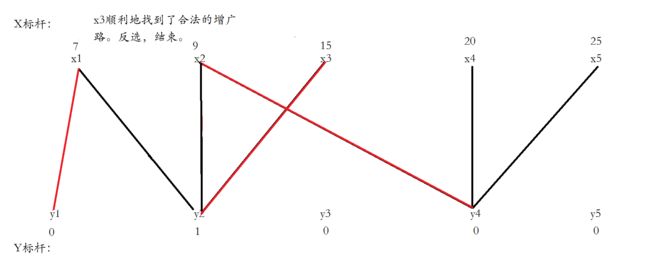
给x3找一个合法的增广路，一下就找到了，直接反选，结束。





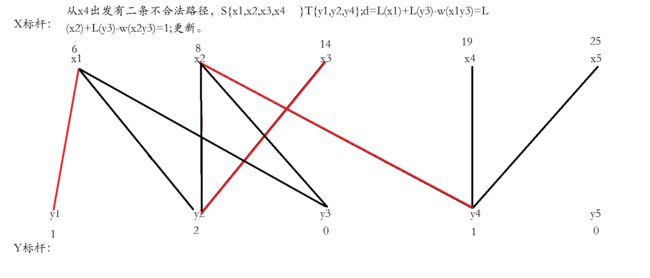
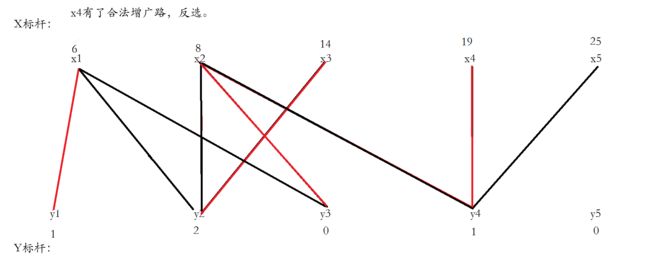
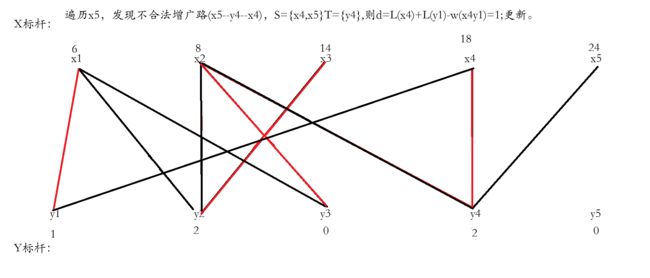
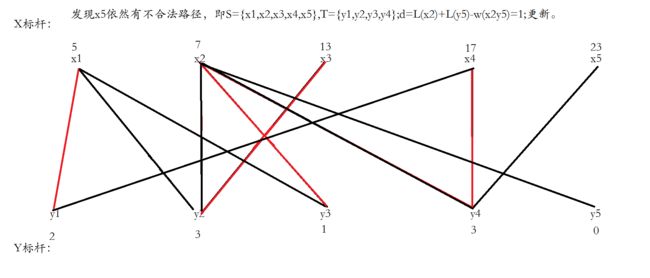
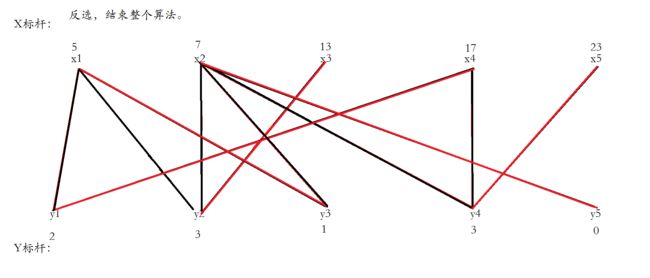
之后的步骤就如同图上所说。
代码已经写出：

#include <iostream>
#include <ctime>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <iomanip>
#include <stack>
using namespace std;
int w[1005][1005];
const int inf=(1<<20)-1;
int m,n;//n左m右 
int cx[1005],cy[1005];//顶标 
bool usex[1005],usey[1005];//本回合使用的x，y 
int link[1005];//link[i]=x代表：在y图中的i与x相连 
bool dfs(int u){
    usex[u]=1;
    for(int i=1;i<=m;i++)
        if(!usey[i]&&cx[u]+cy[i]==w[u][i]){
            usey[i]=1;
            if(link[i]==-1||dfs(link[i])){//注意这里要搜link[i]而不是i，因为我们只搜索x侧的，不需要搜索y侧的 
                link[i]=u;
                return 1;   
            }
        }
return 0;
}
int KM(){
    memset(cy,0,sizeof(cy));
    memset(cx,-1,sizeof(cx));
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cx[i]=max(cx[i],w[i][j]);
    for(int i=1;i<=n;i++){      
        while(1){
            int d=inf;
            memset(usex,0,sizeof(usex));
            memset(usey,0,sizeof(usey));
            if(dfs(i))break;
            for(int i=1;i<=n;i++)
                if(usex[i])
                    for(int j=1;j<=m;j++)
                        if(!usey[j])d=min(d,cx[i]+cy[j]-w[i][j]);
            if(d==inf)return -1;
            for(int i=1;i<=n;i++)
                if(usex[i])cx[i]-=d;
            for(int i=1;i<=m;i++)
                if(usey[i])cy[i]+=d;
        }
    }
    int ans=0;
    for(int i=1;i<=m;i++){
        if(~link[i])ans+=w[link[i]][i];
    }
    return ans; 
}
int main (){
    while(~scanf("%d%d",&n,&m)){
        memset(w,0,sizeof(w));
        memset(link,-1,sizeof(link));
        int a,b,c;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                scanf("%d",&w[i][j]);               
        printf("%d\n",KM());
    }   
    return 0;
}