【CODEFORCES】 C. Kamal-ol-molk's Painting
题解:这一题我已经写吐了,从中午一直写到现在,代码写的又长又乱,思路也很杂,应该有更好的办法能解决,等过几天看了题解在补出来,先写下自己的做法。
以下几点是不合法的情况:
一、因为这是一把长方形的刷子,只能往下或者往右,所以如果我从这个图形的边界走(只往下或往右),一定可以组成一个封闭的图形。如果不行,则输出-1.
二、因为是刷子,所以整个图只有可能存在一个封闭的X区域,比如这种情况:
4 4
XX..
XX..
XX..
...X
这样就是不行的,所以从第一个点广搜。搜完后如果还有没搜到的点,输出-1。
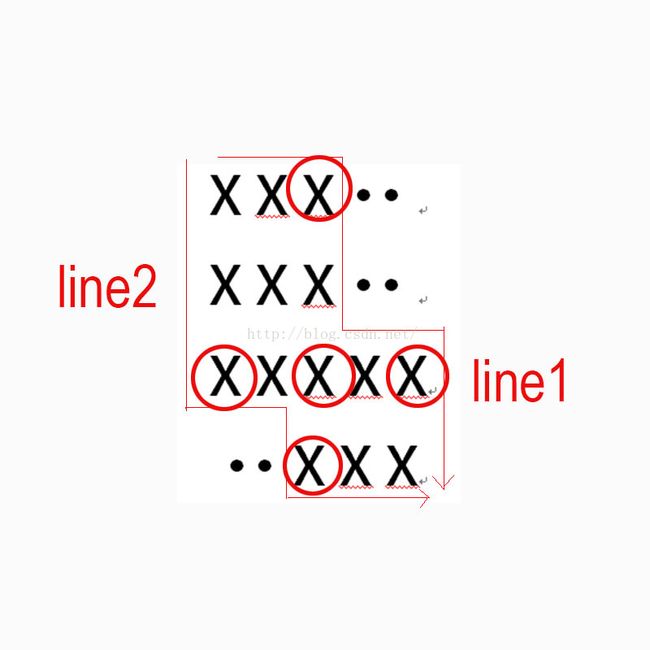
三、我们在边界上定义一种点叫做拐点,图中已画出,我们把line1上的拐点和line2上的拐点记录下来,这样,line1和line2同方向的拐点就是刷子的两个对角,如果存在一组对角的面积与前面的对角计算出来的面积不相等的话就输出-1。
接下来说说可能的情况
一、首先刷子可能没有拐弯,所以最后的情况就是矩形,我们找出矩形长宽的最小值就可以了。
二、刷子拐弯了,纳闷我们先找出两条线上的拐点,然后针对拐点的情况作分析。
1、如果某一条线上只有一个拐点或拐点比另一条线上的少,且此时的形状不是矩形,那么另一条线上的第二个怪拐点一定是与之相对的对角(具体可以画画看,这里不说了....而且这个思路的本质是想知道刷子最初是向左还是向右)所以计算此时面积,然后计算后面对角的面积,如果不等,就输出-1,否则就是答案。(上面第三点)
2、如果两条线拐点相等,那么久不能判断刷子一开始是向左还是向右,所以都要算,如果两种情况有一种可以,那就是答案,如果都不行,那就输出-1。
哗啦一大堆也不知道说清楚了没.....等过几天思路更加清晰了再补回来....
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
using namespace std;
char s[1005][1005];
int n,m,h1,h2,ans,flag[1005][1005];
struct line
{
int x,y;
} ;
struct line first[1000005],second[1000005],q[1000005];
void bfs(int x,int y)
{
memset(flag,0,sizeof(flag));
int h=0,t=0;
q[t].x=x; q[t].y=y; t++;
flag[x][y]=1;
while (h!=t)
{
if (s[q[h].x+1][q[h].y]=='X' && flag[q[h].x+1][q[h].y]==0)
{
q[t].x=q[h].x+1; q[t].y=q[h].y; t++;
flag[q[h].x+1][q[h].y]=1;
}
if (s[q[h].x][q[h].y+1]=='X' && flag[q[h].x][q[h].y+1]==0)
{
q[t].x=q[h].x; q[t].y=q[h].y+1; t++;
flag[q[h].x][q[h].y+1]=1;
}
h++;
}
}
int Right(int x,int y)
{
if (s[x][y+1]=='X') return 1;
else return 0;
}
int Down(int x,int y)
{
if (s[x+1][y]=='X') return 1;
else return 0;
}
int NO_Way(int x,int y)
{
if (s[x+1][y]!='X' && s[x][y+1]!='X') return 1;
else return 0;
}
int construct()
{
int x,y,i,j,f=0;
for ( i=0;i<n;i++)
{
for ( j=0;j<m;j++) if (s[i][j]=='X')
{
x=i; y=j; f=1;
break;
}
if (f) break;
}
i=x; j=y; f=0;
bfs(x,y);
for (int i=0;i<n;i++)
for (int j=0;j<m;j++)
if (s[i][j]=='X' && !flag[i][j]) return 0;
while (Right(i,j)) j++;
first[h1].x=i; first[h1].y=j; h1++; f=1;
while (!NO_Way(i,j))
{
if (Down(i,j))
{
if (!f) { first[h1].x=i; first[h1].y=j; h1++; f=1; }
i++;
}
while (Right(i,j))
{
if (f) { first[h1].x=i; first[h1].y=j; h1++; f=0; }
j++;
}
}
int x1=i,y1=j;
i=x; j=y;
while (Down(i,j)) i++; f=0;
second[h2].x=i; second[h2].y=j; h2++; f=1;
while (!NO_Way(i,j))
{
if (Right(i,j))
{
if (!f) { second[h2].x=i; second[h2].y=j; h2++; f=1; }
j++;
}
while(Down(i,j))
{
if (f) { second[h2].x=i; second[h2].y=j; h2++; f=0; }
i++;
}
}
//check
if (x1!=i || y1!=j) return 0;
else return 1;
}
int area(int i,int j)
{
int h=abs(first[i].x-second[j].x)+1;
int w=abs(first[i].y-second[j].y)+1;
return h*w;
}
int main()
{
scanf("%d%d",&n,&m);
for (int i=0;i<n;i++)
scanf("%s",s[i]);
if (!construct())
{
cout <<-1<<endl;
return 0;
}
//Rectangle
if (h1==h2 && h1==1)
{
cout <<min(abs(first[0].x-second[0].x)+1,abs(first[0].y-second[0].y)+1)<<endl;
return 0;
}
if (h1==1 || h1<h2)
{
ans=area(0,1);
for (int i=0;i<h1;i++) if (ans!=area(i,i+1))
{
cout <<-1<<endl;
return 0;
}
}
else if (h2==1 || h2<h1)
{
ans=area(1,0);
for (int i=0;i<h2;i++) if (ans!=area(i+1,i))
{
cout <<-1<<endl;
return 0;
}
}
else
{
int k1=0,k2=0;
ans=area(0,1);
for (int i=0;i<h1-1;i++) if (ans!=area(i,i+1)) {k1=1; break;}
ans=area(1,0);
for (int i=0;i<h2-1;i++) if (ans!=area(i+1,i)){k2=1; break;}
if (k1 && k2)
{
cout <<-1<<endl;
return 0;
}
else if (!k1 && !k2) ans=min(area(1,0),area(0,1));
else if (!k1) ans=area(0,1);
else if (!k2) ans=area(1,0);
}
cout <<ans<<endl;
return 0;
}