codeforce 22#div2E
题目大意
给了 n(2<=n<=105) 个点,从每个点 u 出发连向了一个点 v(共 n 条边)
现在要求添加最少的边使得整个图是一个强连通图
做法分析
这道题千万不要一般化:先求强连通分量再把图化为 DAG 来做(我们能够很方便的得到需要添加的边的数量,但是加哪些边会变得很麻烦)
注意一个细节:每个点的出度必为 1
有什么特点?
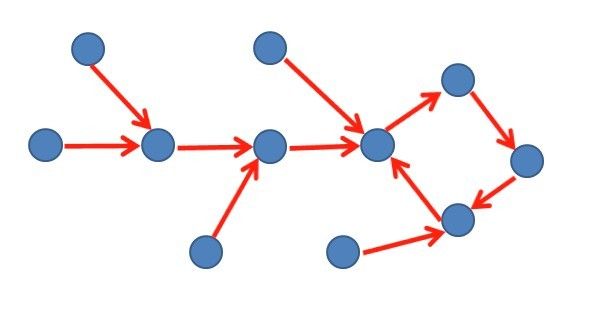
从一个点 u 出发 DFS 遍历所有能够遍历到的点,DFS 结束的时候必定得到一个环!而且,因为每个点的出度为 1,所有遍历到的点只能形成一个环!而且这个环还是在路径的结尾,如果把这个换缩成一个点,那么我们等够得到的是一个“倒着长”的树(只存在从叶子节点到树根的节点,这个环缩成树根了)
如下面的图:
我们把所有的点作为起点 DFS 一遍之后就会得到一系列的这种图,当然,还有一种特殊情况:环!为了便于讲述,我们把它们叫做“分块”
给每个定义一个起点和终点,然后按照下面的做就行了:
当整个图只有一个环的时候,不可能通过加边使得其成为强连通图!
链接相邻的两个分块(分块 A 的终点连向分块 B 的起点)
对于分块中不是起点的入度为 0 的点,建一条反向边
好了,这样加边之后,整个图就以最小的加边数量变成强连通图了
最开始我找出来了强连通分量,然后找出出度为0,入度为0 ,以及出入度都为0的缩点,但是只过了15组数据,后来改来改去只过了10组数据,不知道哪里的问题,希望有大神可以指点一下,我的错误代码:
#include <iostream>
#include <stdio.h>
#include <string>
#include <string.h>
#include <vector>
const int maxn=200200,maxm=500400;
using namespace std;
struct Edge
{
int x,y,next;
} e[maxm];
int num[maxn];///每个连通分量含有点个数
int dfn[maxn],low[maxn],v[maxn],s[maxn],b[maxn],h[maxn];
int tot=0,cnt=0,times,t;
int n,m;
void init()
{
tot=0;
memset(h,0,sizeof(h));
}
void add(int x,int y)
{
e[++tot].x=x;
e[tot].y=y;
e[tot].next=h[x];
h[x]=tot;
}
int max(int a,int b)
{
if(a>b)
return a;
return b;
}
int min(int a,int b)
{
if(a>b)
return b;
return a;
}
void Tarjan(int x)
{
int y,i;
times++;
t++;
dfn[x]=low[x]=times;
v[x]=1;
s[t]=x;
for( i=h[x]; i; i=e[i].next)
{
y=e[i].y;
if(v[y]==0)
{
Tarjan(y);
low[x]=min(low[x],low[y]);
}
if(v[y]==1)
low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x])
{
cnt++;
do
{
y=s[t--];
b[y]=cnt;///属于哪个强连通分量,cnt也是强连通分量个数1-cnt
v[y]=2;
num[cnt]++;
}
while(y!=x);
}
}
void solve(int n)
{
times=0;
t=0;
cnt=0;
memset(dfn,0,sizeof(dfn));
memset(num,0,sizeof(num));
memset(v,0,sizeof(v));
for(int i=1; i<=n; i++)
if(!dfn[i])
Tarjan(i);
}
int In[maxn],Out[maxn];
int Uin[maxn],Uout[maxn],Uiu[maxn];
vector<int>HD[maxn];
int main()
{
int t;
scanf("%d",&t);
init();
for(int i=1; i<=t; i++)
{
int u;
scanf("%d",&u);
add(i,u);
}
solve(t);
if(cnt==1)
{
puts("0");
return 0;
}
memset(In,0,sizeof(In));
memset(Out,0,sizeof(Out));
memset(Uin,0,sizeof(Uin));
memset(Uout,0,sizeof(Uout));
memset(Uiu,0,sizeof(Uiu));
for(int i=1; i<=t; i++)
{
for(int j=h[i]; j!=0; j=e[j].next)
{
int y=e[j].y;
HD[b[i]].push_back(i);
HD[b[y]].push_back(y);
if(b[i]==b[y])continue;
Out[b[i]]++;
In[b[y]]++;
}
}
int k=0,k2=0,k1=0;
for(int i=1; i<=cnt; i++)
{
if(In[i]==0&&Out[i]==0)
{
Uiu[k++]=i;
}
else
{
if(In[i]==0)
Uin[k1++]=i;
if(Out[i]==0)
Uout[k2++]=i;
}
}
if(k1>k2)
{
printf("%d\n",k1+k*2);
for(int i=0; i<k2; i++)
printf("%d %d\n",HD[Uout[i]][0],HD[Uin[i]][0]);
for(int i=k2; i<k1; i++)
printf("%d %d\n",HD[Uout[0]][0],HD[Uin[i]][0]);
for(int i=0; i<k; i++)
{
printf("%d %d\n",HD[Uin[0]][0],HD[Uiu[i]][0]);
printf("%d %d\n",HD[Uiu[i]][0],HD[Uin[0]][0]);
}
}
else
{
printf("%d\n",k2+k*2);
for(int i=0; i<k1; i++)
printf("%d %d\n",HD[Uout[i]][0],HD[Uin[i]][0]);
for(int i=k1; i<k2; i++)
printf("%d %d\n",HD[Uout[i]][0],HD[Uin[0]][0]);
if(k2!=0)
{
for(int i=0; i<k; i++)
{
printf("%d %d\n",HD[Uout[0]][0],HD[Uiu[i]][0]);
printf("%d %d\n",HD[Uiu[i]][0],HD[Uout[0]][0]);
}
}
else
{
for(int i=0; i<k-1; i++)
{
printf("%d %d\n",HD[Uiu[i]][0],HD[Uiu[i+1]][0]);
printf("%d %d\n",HD[Uiu[i+1]][0],HD[Uiu[i]][0]);
}
}
}
return 0;
}
ac代码,很短,学习的学长的代码:
#include <iostream>
#include <vector>
#include <stdio.h>
#include <string.h>
using namespace std;
const int maxn=200020;
int in[maxn],scl[maxn];
vector <int>e[maxn];
vector<int>In;
vector<int>Out;
int dfs(int u)
{
scl[u]=1;
int v=e[u][0];
if(!scl[v])return scl[u]=dfs(v);
else return scl[u]=u;
}
int main()
{
int n,k,t;
while(~scanf("%d",&n))
{
memset(in,0,sizeof(in));
for(int i=1;i<=n;i++)
{
int u;
scanf("%d",&u);
e[i].push_back(u);
in[u]++;
}
k=0;
memset(scl,0,sizeof(scl));
for(int i=1;i<=n;i++)
{
if(!in[i])
{
k++;
In.push_back(i);
Out.push_back(dfs(i));
}
}
t=k;
for(int i=1;i<=n;i++)
{
if(!scl[i])
{
k++;
In.push_back(i);
Out.push_back(dfs(i));
}
}
if(k==1&&t==0)
k=0;
printf("%d\n",k);
for(int i=0;i<k;i++)
printf("%d %d\n",Out[i],In[(i+1)%k]);
}
// cout << "Hello world!" << endl;
return 0;
}