二分图最大匹配

二分图：二分图是这样一个图，它的顶点可以分类两个集合X和Y，所有的边关联的两个顶点恰好一个属于集合X，另一个属于集合Y。

二分图匹配：给定一个二分图G，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配。
最大匹配：图中包含边数最多的匹配称为图的最大匹配。
完美匹配：如果所有点都在匹配边上，则称这个最大匹配是完美匹配。

二分图匹配基本概念：

未盖点
设VI是G的一个顶点，如果VI不与任意一条属于匹配M的边相关联，就称VI是一个未盖点。
交错轨
   设P是图G的一条轨，如果P的任意两条相邻的边一定是一条属于M而另一条不属于M，就称P是交错轨。
可增广轨（增广路）
    两个端点都是未盖点的交错轨称为可增广轨。

可增广轨的性质：

1：P的路径长度必定为奇数，第一条边和最后一条边都不属于M。
2：P经过取反操作可以得到一个更大的匹配M’。
3：M为G的最大匹配当且仅当不存在相对于M的增广路径。

二分图最大匹配匈牙利算法：

算法的思路是不停的找增广轨,并增加匹配的个数,增广轨顾名思义是指一条可以使匹配数变多的路径,在匹配问题中,增广轨的表现形式是一条"交错轨",也就是说这条由图的边组成的路径,它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且始点和终点还没有被选择过.这样交错进行,显然他有奇数条边.那么对于这样一条路径,我们可以将第一条边改为已匹配,第二条边改为未匹配...以此类推.也就是将所有的边进行"取反",容易发现这样修改以后,匹配仍然是合法的,但是匹配数增加了一对.另外,单独的一条连接两个未匹配点的边显然也是交错轨.可以证明,当不能再找到增广轨时,就得到了一个最大匹配.这也就是匈牙利算法的思路。

 

举例：

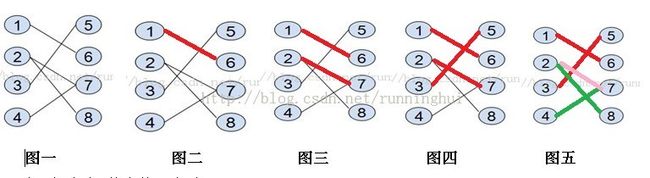
1.  图一为原图（给定的二分图）

2.先从1出发，找到1-6这条增广路 （如图二，匹配的边为红色）

3.从2出发，找到2-7这条增广路（为什么不继续到7-4呢？因为此时7-4还是未匹配的） （如图三）

4.从3 出发找到3-5这条增广路    （如图四）

5.从4出发  4-7这条边还是未匹配的，再看7由于7-2是已经匹配的，于是可以加到4-7-2这条路上（记得联想增广路的定义）  再看2-8这条路是还没有匹配的，于是可以加到4-7-2-8这条路上，从8出发已经找不到与8匹配的结点了，于是4-7-2-8这是一条增广路。注意到这条路有什么特点（当然和增广路一样，未匹配的和匹配的边交替出现，并且始边和终边都是未匹配的。）于是将这条路径上的边取反（即未匹配改为匹配4-7，2-8变为匹配的，2-7变为不匹配的）如图五，于是最终的匹配边为1-6,2-8，3-5，4-7共四个匹配；

代码：

#include <iostream>
using namespace std;
const int MAXN = 1001 ,MAXM = 1001 ;
int n1,n2,m,ans; //n1,n2分别为二分图两边节点的个数,两边的节点分别用1..n1,1..n2编号,m为边数
bool g[MAXN][MAXM]; //图G邻接矩阵g[x][y]
bool y[MAXM]; //Y集合中点i访问标记
int link[MAXM]; //link[y]表示当前与y节点相邻的x节点

void init()
{
    int x,y;
    memset(g,0 ,sizeof (g));
    memset(link,-1 ,sizeof (link));
    ans = 0 ;
    scanf("%d%d%d" ,&n1,&n2,&m); 
    for (int i = 1 ;i <= m;i++)
    {
        scanf("%d%d" ,&x,&y);
        g[x][y] = true ;
    }
}

bool find(int x) //是否存在X集合中节点x开始的增广路
{
    for (int i = 1 ;i <= n2;i++)
        if (g[x][i] && !y[i]) //如果节点i与x相邻并且未访问过
        {
            y[i] = true ;
            if (link[i] == -1 || find(link[i])) //如果找到一个未盖点i中或从与i相邻的节点出发有增广路
            {
                link[i] = x;
                return true ;
            }
        }
    return false ;
}

int main()
{
    init();
    for (int i = 1 ;i <= n1;i++)
    {
        memset(y,0 ,sizeof (y));
        if (find(i))
            ans++;
    }
    printf("%d/n" ,ans);
    return 0 ;
}