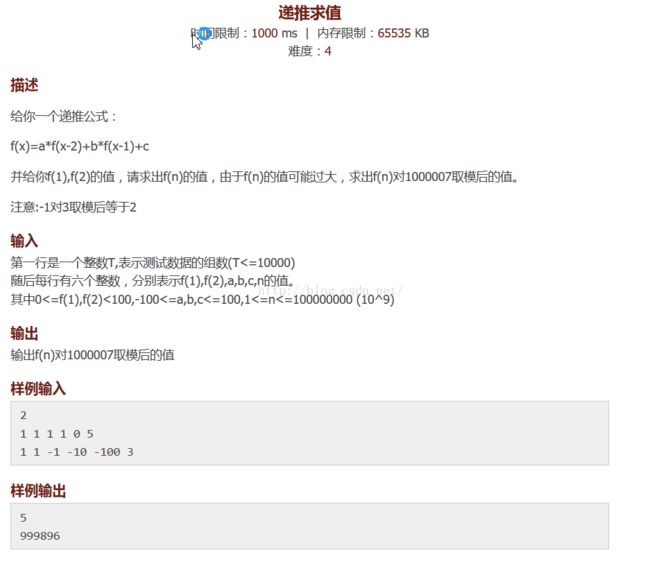
HDU5667 sequence 递推求值 (矩阵快速幂)
容易推出上面的矩阵递推式,而且我们知道 f1,f2的值,对中间的矩阵进行快速幂运算就能快速得到结果了。
类似的入门题:http://blog.csdn.net/chaiwenjun000/article/details/50808722
trick ,这个题对负数的取模有自己的规定,需要注意一下。(I64d超时 要用lld。。。)
#include<iostream>
#include<vector>
#include<queue>
#include<cstdio>
#include<cstring>
#define INF 99999999
using namespace std;
const int maxn = 3;
typedef long long ll;
struct matrix{
ll G[maxn][maxn];
};
int mod;int n = 3;
matrix Mul(matrix A,matrix B){
matrix ans;
memset(ans.G,0,sizeof(ans.G)); // 不要忘了初始化
for(int i=0;i<n;i++)
for(int k=0;k<n;k++){
for(int j=0;j<n;j++)
ans.G[i][j] = (ans.G[i][j] + A.G[i][k] * B.G[k][j]) % mod;
}
return ans;
}
matrix Pow(matrix A,ll b){
matrix ans;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ans.G[i][j] =(i == j);
while(b){
if(b & 1)
ans = Mul(ans,A);
A = Mul(A,A);
b>>=1;
}
return ans;
}
int main(){
int t; scanf("%d",&t);
mod = 1000007;
while(t--){
ll f1,f2,a,b,c,n;
scanf("%lld%lld%lld%lld%lld%lld",
&f1,&f2,&a,&b,&c,&n);
matrix pre,m;
memset(pre.G,0,sizeof(pre.G));
memset(m.G,0,sizeof(m.G));
pre.G[0][0] = f2,pre.G[1][0] = f1,pre.G[2][0] = 1;
m.G[0][0] = b,m.G[0][1] = a,m.G[0][2] = c;
m.G[1][0] = m.G[2][2]= 1;
if(n == 1){
printf("%lld\n",(f1+mod)%mod);
}
else if(n == 2){
printf("%lld\n",(f2+mod)%mod);
}
else{
matrix p = Pow(m,n-2);
pre = Mul(p,pre);
printf("%lld\n",(pre.G[0][0]+mod)%mod);
}
}
}
hdu 5667 sequence
可以发现所有的公式都可以表示成 a的幂的形式,对于a的幂
可以推出公式 gi = b*(c * gi-1 + gi-2); 对这个公式运用矩阵快速幂即可。
因为是对幂的取模, 所以取得模应该是 p的欧拉函数,又因为p是素数,所以phi(p) = p - 1;
a ^ b % c = a ^(b % phi(c) + phi(c)) % c;
注意,我们用矩阵快速幂求得 b % phi(c)之后,还要加上 phi(c);
#include<iostream>
#include<vector>
#include<queue>
#include<cstdio>
#include<cstring>
#define INF 99999999
using namespace std;
const int maxn = 3;
typedef long long ll;
struct matrix{
ll G[maxn][maxn];
};
int mod;int n = 3;
ll pow_mod(ll x,ll n,ll mod){
ll ans = 1;
x%=mod;
while(n){
if(n &1) ans = ans *x %mod;
x = x * x%mod;
n/=2;
}
return ans;
}
matrix Mul(matrix A,matrix B){
matrix ans;
memset(ans.G,0,sizeof(ans.G)); // 不要忘了初始化
for(int i=0;i<n;i++)
for(int k=0;k<n;k++){
for(int j=0;j<n;j++){
ans.G[i][j] = (ans.G[i][j] + A.G[i][k] * B.G[k][j]) % (mod-1);//取模mod的欧拉函数
}
}
return ans;
}
matrix Pow(matrix A,ll b){
matrix ans;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ans.G[i][j] =(i == j);
while(b){
if(b & 1)
ans = Mul(ans,A);
A = Mul(A,A);
b>>=1;
}
return ans;
}
int main(){
int t; scanf("%d",&t);
while(t--){
ll n,a,b,c,p;
scanf("%I64d%I64d%I64d%I64d%I64d",
&n,&a,&b,&c,&p);
mod = p;
matrix pre,m;
memset(pre.G,0,sizeof(pre.G));
memset(m.G,0,sizeof(m.G));
pre.G[0][0] = b,pre.G[1][0] = 0,pre.G[2][0] = 1;
m.G[0][0] = c,m.G[0][1] = 1,m.G[0][2] = b;
m.G[1][0] = m.G[2][2]= 1;
if(n == 1){
printf("1\n");
}
else if(n == 2){
printf("%I64d\n",pow_mod(a,b,mod));
}
else{
matrix p = Pow(m,n-2);
// ll mi = p.G[0][0] * b + p.G[0][2] ;
pre = Mul(p,pre);
ll mi = pre.G[0][0] + mod-1; //加上mod -1
ll ans = pow_mod(a,mi,mod);
printf("%I64d\n",ans);
}
}
}