HDU-4565 So Easy!(数学&&矩阵快速幂)
So Easy!
http://acm.hdu.edu.cn/showproblem.php?pid=4565
Problem Description
A sequence S
n is defined as:
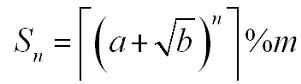
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S n.
You, a top coder, say: So easy!

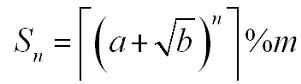
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S n.
You, a top coder, say: So easy!

Input
There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2
15, (a-1)
2< b < a
2, 0 < b, n < 2
31.The input will finish with the end of file.
Output
For each the case, output an integer S
n.
Sample Input
2 3 1 2013 2 3 2 2013 2 2 1 2013
Sample Output
4 14 4
貌似去年网络赛还是多校见过类似的题,但是没有补题,所以依旧不会,只记得见过...
这题只难在推导递推公式,其他还好吧,看到这个数学推导,发现高中真是虚度,什么都不会
详细推导过程:http://blog.csdn.net/ljd4305/article/details/8987823
#include <cstdio>
#include <cstring>
using namespace std;
const int MAXN=2;
struct Matrix {
long long x[MAXN][MAXN];
Matrix() {
memset(x,0,sizeof(x));
}
}cur;
long long a,b,n,mod;
Matrix mul(const Matrix& x,const Matrix& y) {
Matrix c;
for(int i=0;i<MAXN;++i)
for(int j=0;j<MAXN;++j)
for(int k=0;k<MAXN;++k)
c.x[i][j]=(c.x[i][j]+x.x[i][k]*y.x[k][j])%mod;
return c;
}
Matrix quick_pow(Matrix x,long long num) {//矩阵快速幂
Matrix ans;
for(int i=0;i<MAXN;++i)
ans.x[i][i]=1;
while(num>0) {
if((num&1)==1)
ans=mul(ans,x);
x=mul(x,x);
num>>=1;
}
return ans;
}
int main() {
while(4==scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&mod)) {
if(n==1) {
printf("%I64d\n",(a<<1)%mod);
continue;
}
if(n==2) {
printf("%I64d\n",((a*a+b)<<1)%mod);
continue;
}
cur.x[0][0]=a<<1;
cur.x[0][1]=1;
cur.x[1][0]=b-a*a;
while(cur.x[1][0]<0)//防止负数产生错误答案,刚开始只加了1次mod,结果还是WA,完全没想到会这么小...
cur.x[1][0]+=mod;
cur.x[1][1]=0;
cur=quick_pow(cur,n-2);//cur为右乘的矩阵
printf("%I64d\n",(2*(a*a+b)*cur.x[0][0]+2*a*cur.x[1][0])%mod);
}
return 0;
}