HDUOJ 1198 Farm Irrigation(并查集)
Farm Irrigation
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 2167 Accepted Submission(s): 977
Problem Description
Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.
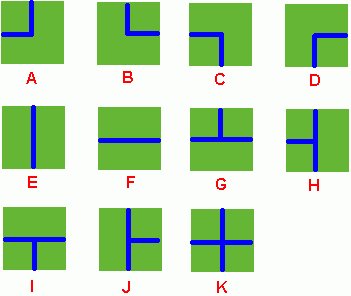
Figure 1
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map
ADC
FJK
IHE
then the water pipes are distributed like
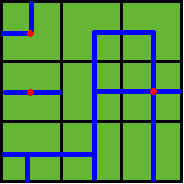
Figure 2
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.
Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?
Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

Figure 1
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map
ADC
FJK
IHE
then the water pipes are distributed like

Figure 2
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.
Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?
Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.
Input
There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.
Output
For each test case, output in one line the least number of wellsprings needed.
Sample Input
2 2 DK HF 3 3 ADC FJK IHE -1 -1
Sample Output
2 3
Author
ZHENG, Lu
Source
Zhejiang University Local Contest 2005
关于并查集,只在kruskal算法里面用到过,这是第一次独立完成并查集的题目,存此留念。
思路:每一个方格设东西南北四道门,用flag表示,1代表有水管连接,0代表木有。我合并集合的方法有点暴力,就是Union函数中暴力搜索所有方块。这样做是考虑到M、N均不大于50,所以这个方法耗时不多,以下的AC code用时62MS。
我本来想用scanf输入的,但由于scanf输入字符时识别换行符,所以不用。
AC code:
#include <iostream>
#include <cstdio>
#include <memory.h>
using namespace std;
const int N=50;
int n,m,i,j,k,well[N][N];
char a[N][N];
bool flag[N][4*N];
void func(char ch)
{
k=4*j;
if(ch=='A') flag[i][k]=flag[i][k+3]=1;
else if(ch=='B') flag[i][k]=flag[i][k+1]=1;
else if(ch=='C') flag[i][k+2]=flag[i][k+3]=1;
else if(ch=='D') flag[i][k+1]=flag[i][k+2]=1;
else if(ch=='E') flag[i][k]=flag[i][k+2]=1;
else if(ch=='F') flag[i][k+1]=flag[i][k+3]=1;
else if(ch=='G') flag[i][k]=flag[i][k+1]=flag[i][k+3]=1;
else if(ch=='H') flag[i][k]=flag[i][k+2]=flag[i][k+3]=1;
else if(ch=='I') flag[i][k+1]=flag[i][k+2]=flag[i][k+3]=1;
else if(ch=='J') flag[i][k]=flag[i][k+1]=flag[i][k+2]=1;
else if(ch=='K') flag[i][k]=flag[i][k+1]=flag[i][k+2]=flag[i][k+3]=1;
}
void Union(int x,int y)
{
int ii,jj;
if(x>y)
{
for(ii=0;ii<m;ii++)
{
for(jj=0;jj<n;jj++)
{
if(well[ii][jj]==x) well[ii][jj]=y;
}
}
}
else
{
for(ii=0;ii<m;ii++)
{
for(jj=0;jj<n;jj++)
{
if(well[ii][jj]==y) well[ii][jj]=x;
}
}
}
}
int main()
{
int count;
while(scanf("%d%d",&m,&n)!=EOF && m>0)
{
if(n==1 && m==1)
{
cin>>a[0][0];
count=1;
}
else
{
count=m*n;
memset(flag,false,sizeof(flag));
//初始化well,使得方块之间属于独立的集合
for(i=0,k=0;i<m;i++)
for(j=0;j<n;j++)
{
well[i][j]=k;
k++;
}
for(i=0;i<m;i++)
for(j=0;j<n;j++)
{
cin>>a[i][j];
func(a[i][j]);
}
//同一行向右横向比较,同一列向下纵向比较
for(i=0;i<m-1;i++)
{
for(j=0;j<n-1;j++)
{
k=4*j;
//同一行
if(flag[i][k+1]==1 && flag[i][k+7]==1 && well[i][j+1]!=well[i][j])
{
Union(well[i][j],well[i][j+1]);
count--;
}
//同一列
if(flag[i][k+2]==1 && flag[i+1][k]==1 && well[i+1][j]!=well[i][j])
{
Union(well[i+1][j],well[i][j]);
count--;
}
}
}
//最后一行只作行的比较
for(i=m-1,j=0;j<n-1;j++)
{
k=4*j;
if(flag[i][k+1]==1 && flag[i][k+7]==1 && well[i][j+1]!=well[i][j])
{
Union(well[i][j],well[i][j+1]);
count--;
}
}
//最后一列只作列的比较
for(j=n-1,i=0,k=4*j;i<m-1;i++)
{
if(flag[i][k+2]==1 && flag[i+1][k]==1 && well[i+1][j]!=well[i][j])
{
Union(well[i][j],well[i+1][j]);
count--;
}
}
}
printf("%d\n",count);
}
return 0;
}