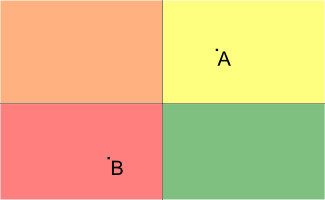
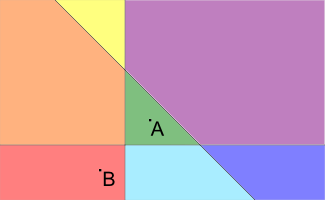
计算几何。
求有多少直线与AB的交点的横坐标在AB之间。
要注意除数为0的情况!!
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <cmath>
#include <cstdio>
#define eps 1e-9
using namespace std;
int main()
{
double x1,x2,y1,y2;
int n;
scanf("%lf%lf",&x1,&y1);
scanf("%lf%lf",&x2,&y2);
if (fabs(x1-x2)<eps)
{
int ans=0;
cin>>n;
if (y1>y2) swap(x1,x2),swap(y1,y2);
for (int i=1;i<=n;i++)
{
double ai,bi,ci;
cin>>ai>>bi>>ci;
if (fabs(bi-0.0)<eps)
continue;
else
{
double y=-(ci+ai*x1)/bi;
if (y>y1-eps&&y<y2+eps)
ans++;
}
}
cout<<ans<<endl;
return 0;
}
if (x1>x2) swap(x1,x2),swap(y1,y2);
double k=(y1-y2)/(x1-x2);
double b=y1-k*x1;
scanf("%d",&n);
int ans=0;
for (int i=1;i<=n;i++)
{
double ai,bi,ci;
scanf("%lf%lf%lf",&ai,&bi,&ci);
double x;
if (fabs(bi-0.0)<eps)
x=(-ci)/ai;
else
{
ai/=bi,ci/=bi,bi=1.0;
if (fabs(k+ai-0.0)<eps) continue;
x=-(ci+b)/(k+ai);
}
if (x>x1-eps&&x<x2+eps)
ans++;
}
cout<<ans<<endl;
return 0;
}
It turns out that you are a great fan of rock band AC/PE. Peter learned that and started the following game: he plays the first song of the list of n songs of the group, and you have to find out the name of the song. After you tell the song name, Peter immediately plays the following song in order, and so on.
The i-th song of AC/PE has its recognizability pi. This means that if the song has not yet been recognized by you, you listen to it for exactly one more second and with probability of pi percent you recognize it and tell it's name. Otherwise you continue listening it. Note that you can only try to guess it only when it is integer number of seconds after the moment the song starts playing.
In all AC/PE songs the first words of chorus are the same as the title, so when you've heard the first ti seconds of i-th song and its chorus starts, you immediately guess its name for sure.
For example, in the song Highway To Red the chorus sounds pretty late, but the song has high recognizability. In the song Back In Blue, on the other hand, the words from the title sound close to the beginning of the song, but it's hard to name it before hearing those words. You can name both of these songs during a few more first seconds.
Determine the expected number songs of you will recognize if the game lasts for exactly T seconds (i. e. you can make the last guess on the second T, after that the game stops).
If all songs are recognized faster than in T seconds, the game stops after the last song is recognized.
Output
Output a single number — the expected number of the number of songs you will recognize in T seconds. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
期望dp。
f[i][j]表示在第j秒的时候辨认出第i首歌的可能性。
而这首歌可能是第1,2,3..t[i]秒,如果依次枚举的话就O(n^3)了。
但是我们发现i秒是可以从i-1秒转移过来的!乘上(1-p[i])再加上f[i-1][j]。
但是要注意最后一秒一定可以听出来,要特殊处理。
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
int t[5500],n,T;
double p[5500],f[5500][5500];
int main()
{
scanf("%d%d",&n,&T);
for (int i=1;i<=n;i++)
{
scanf("%lf%d",&p[i],&t[i]);
p[i]=(double)(p[i]/100);
}
f[0][0]=1.0;
double ans=0.0;
for (int i=1;i<=n;i++)
{
double x=0.0,k=pow(1.0-p[i],t[i]-1);
for (int j=i;j<=T;j++)
{
x=x*(1.0-p[i])+f[i-1][j-1];
if (j>=t[i])
{
x-=f[i-1][j-t[i]]*k;
f[i][j]=x*p[i]+f[i-1][j-t[i]]*k;
}
else
f[i][j]=x*p[i];
ans+=f[i][j];
}
}
printf("%.9lf\n",ans);
return 0;
}
二分图最大匹配。
题目中说ik+jk是奇数,那么这些点符合二分图性质(左边是奇数右边是偶数即可)。
把每个数质数拆分,能拆成多个p[i]的话也要拆成多个点;
然后对于有边相连的数的相同质数连边。
最大匹配就是答案。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <vector>
#define pb push_back
#define mp make_pair
#define f first
#define s second
using namespace std;
vector<pair<int,int> > v[2];
int tot=1,u[105][105],h[100005],cnt=0;
int my[10000],check[100005],a[105],ti,p[100000],V[10000];
struct edge
{
int y,ne;
}e[100000];
void Prepare()
{
for (int i=2;i<=100000;i++)
if (!check[i])
{
p[++cnt]=i;
for (int j=i;j<=100000;j+=i)
check[j]=1;
}
}
void chai(int x)
{
for (int i=1;i<=cnt;i++)
if (a[x]!=1)
{
while (a[x]%p[i]==0)
{
a[x]/=p[i];
v[x%2].pb(mp(x,p[i]));
}
}
if (a[x]>1)
v[x%2].pb(mp(x,a[x]));
}
void Addedge(int x,int y)
{
e[++tot].y=y;
e[tot].ne=h[x];
h[x]=tot;
}
bool dfs(int x)
{
for (int i=h[x];i;i=e[i].ne)
{
int y=e[i].y;
if (V[y]!=ti)
{
V[y]=ti;
if (!my[y]||dfs(my[y]))
{
my[y]=x;
return true;
}
}
}
return false;
}
int main()
{
Prepare();
int n,m;
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
scanf("%d",&a[i]),chai(i);
for (int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
u[x][y]=u[y][x]=1;
}
int l=v[0].size();
for (int i=0;i<v[0].size();i++)
for (int j=0;j<v[1].size();j++)
if (u[v[0][i].f][v[1][j].f]&&v[0][i].s==v[1][j].s)
Addedge(i+1,j+1+l);
int ans=0;
for (int i=1;i<=l;i++)
{
ti++;
if (dfs(i)) ans++;
}
cout<<ans<<endl;
return 0;
}
感悟:
1.计算几何要注意除数为0
2.如果满足二分图性质的想最大匹配