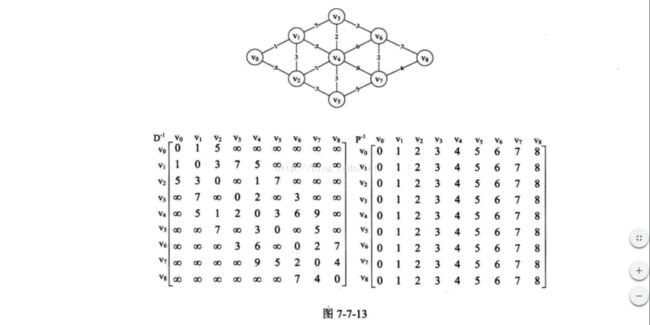
最短路径（弗洛伊德算法）

1 原理 ，假设存在一个最简单的连通图

2 代码

package leaning.graph;

/*
 * 
 * 弗洛伊德算法求最短路径
 * 
 * */
public class Floyd {

	    // 表示V0顶点到v8顶点的最短路径的值
		private int[][] D = new int[9][9]; 
		
		// 最短路径节点走法
		private  int[][] P = new int[9][9]; 
		
		//定义无穷大的数
		private int MAX = Integer.MAX_VALUE/2;
		
		//定义地图变量
		private int[][] map = new int[9][9];
		
		//定义顶点变量
		private String[] points = {"v0","v1","v2","v3","v4","v5","v6","v7","v8"};
		
		//初始化地图
		public void createMap(){
			this.map[0] = new int[]{  0,  1,  5,MAX,MAX,MAX,MAX,MAX,MAX};
			this.map[1] = new int[]{  1,  0,  3,  7,  5,MAX,MAX,MAX,MAX};
			this.map[2] = new int[]{  5,  3,  0,MAX,  1,  7,MAX,MAX,MAX};
			this.map[3] = new int[]{MAX,  7,MAX,  0,  2,MAX,  3,MAX,MAX};
			this.map[4] = new int[]{MAX,  5,  1,  2,  0,  3,  6,  9,MAX};
			this.map[5] = new int[]{MAX,MAX,  7,MAX,  3,  0,MAX,  5,MAX};
			this.map[6] = new int[]{MAX,MAX,MAX,  3,  6,MAX,  0,  2,  7};
			this.map[7] = new int[]{MAX,MAX,MAX,MAX,  9,  5,  2,  0,  4};
			this.map[8] = new int[]{MAX,MAX,MAX,MAX,MAX,MAX,  7,  4,  0};
		}
		
		//初始化变量
		public void iniVar(){
			for(int v = 0 ; v < this.points.length ; v++){
				for(int w = 0 ; w < this.points.length ; w++){
					this.D[v][w] = this.map[v][w];
					this.P[v][w] = w;
				}
			}
		}
		
		/*
		 * 弗洛伊德算法核心
		 * 参数 startPoint 为起始点
		 * 参数 endPoint 为终点
		 * */
		public void floydCore(String startPoint,String endPoint){
			// 1 初始化变量
			this.createMap();
			this.iniVar();
			// 2 循环
			for(int k = 0 ; k < this.points.length ; k++){
				for( int v = 0 ; v < this.points.length ;v++){
					for(int w = 0 ; w < this.points.length ;w++){
						if(this.D[v][w] > this.D[v][k] + this.D[k][w]){
							this.D[v][w] = this.D[v][k] + this.D[k][w];
							this.P[v][w] = this.P[v][k]; 
						}
					}
				}
			}
			// 3 输出结果
			this.show(startPoint,endPoint);
		}
	
		//根据名称得到它的位置
		public int getNumber(String pointName){
			int position = -1;
			for(int i = 0 ;  i < this.points.length ;i++  ){
				if(this.points[i].endsWith(pointName.replace(" ", ""))){
					position = i;
					break;
				}
			}
			return position;
		}
		// 得到v0顶点到pointName顶点的路径
		public String getPath(String startPointName,String endPointName){
			//初始化变量
			StringBuffer path = new StringBuffer();
			int startPosition = this.getNumber(startPointName);
			int endPosition = this.getNumber(endPointName);
			// 得到path值
			path.append(startPointName);
			int cenPosition = this.P[startPosition][endPosition];
			while(cenPosition!=endPosition){
				path.append("->"+this.points[cenPosition]);
				cenPosition = this.P[cenPosition][endPosition];
			}
			path.append("->"+endPointName);
			return path.toString();
		}
		
		//输出结果
		public void show(String startPointName,String endPointName){
			// 1  输出权值大小
			int startPosition = this.getNumber(startPointName);
			int endPosition = this.getNumber(endPointName);
			System.out.println("节点"+startPointName+"到节点"+endPointName+":");
			System.out.println("最小权值为  : " + this.D[startPosition][endPosition]);
			// 2  输出路径
			System.out.println("路径为 : " + this.getPath(startPointName, endPointName));
		}
		
	    public static void main(String[] args) {
	    	Floyd floyd = new Floyd();
	    	floyd.floydCore("v0","v8");
	    }

}

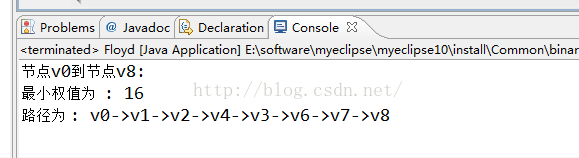
3  输出结果